← return to practice.dsc10.com
These problems are taken from past quizzes and exams. Work on them
on paper, since the quizzes and exams you take in this
course will also be on paper.
We encourage you to complete these
problems during discussion section. Solutions will be made available
after all discussion sections have concluded. You don’t need to submit
your answers anywhere.
Note: We do not plan to cover all of
these problems during the discussion section; the problems we don’t
cover can be used for extra practice.
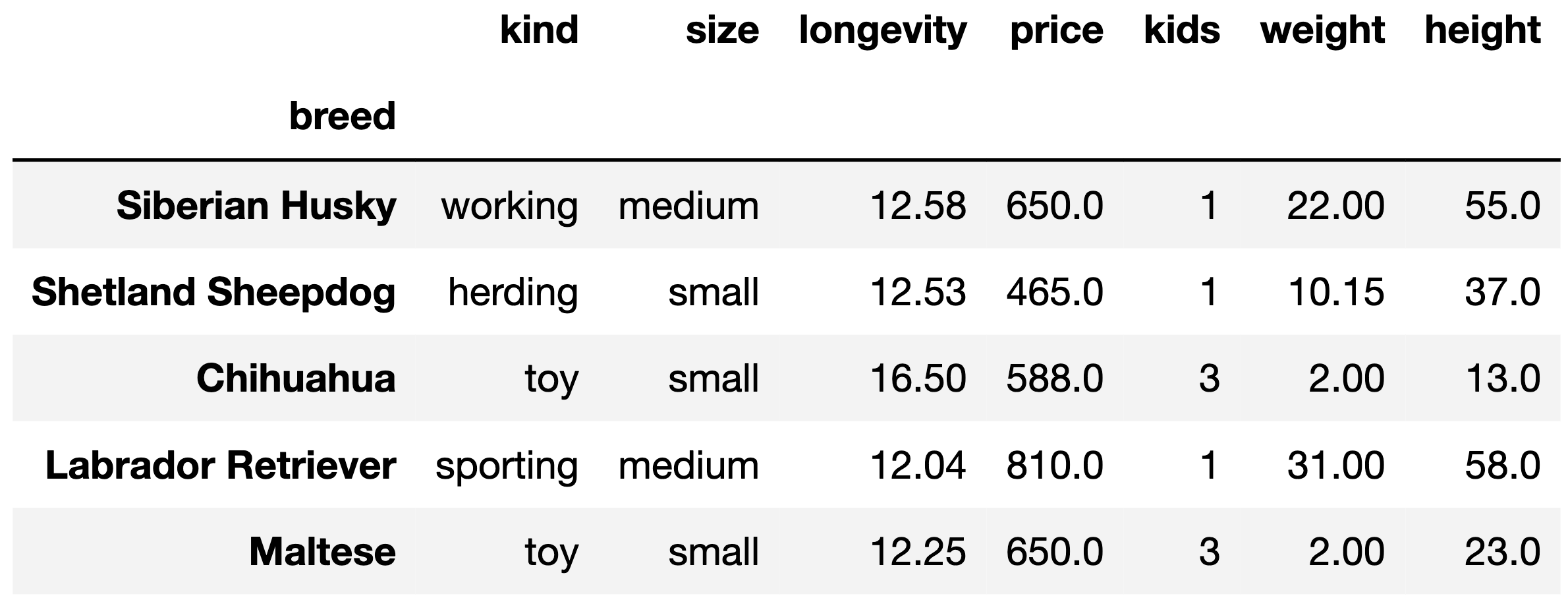
df. The index of df contains the dog breed
names as str values.
The columns are:
'kind' (str): the kind of dog (herding, hound, toy,
etc.). There are six total kinds.'size' (str): small, medium, or large.'longevity' (float): typical lifetime (years).'price' (float): average purchase price (dollars).'kids' (int): suitability for children. A value of
1 means high suitability, 2 means medium, and
3 means low.'weight' (float): typical weight (kg).'height' (float): typical height (cm).The rows of df are arranged in no particular
order. The first five rows of df are shown below
(though df has many more rows than
pictured here).

Assume we have already run import babypandas as bpd and
import numpy as np.
The following code computes an array containing the unique kinds of dogs that are heavier than 20 kg or taller than 40 cm on average.
foo = df.__(a)__.__(b)__
np.array(foo[__(c)__].__d__)Fill in blank (a).
Answer: groupby('kind')
We start this problem by grouping the dataframe by
'kind' since we’re only interested in whether each unique
'kind' of dog fits some sort of constraint. We don’t quite
perform querying yet since we need to group the DataFrame first. In
other words, we first need to group the DataFrame into each
'kind' before we could apply any sort of boolean
conditionals.
The average score on this problem was 97%.
Fill in blank (b).
Answer: .mean()
After we do .groupby('kind'), we need to apply
.mean() since the problem asks if each unique
'kind' of dog satisfies certain constraints on
average. .mean() calculates the average of each
column of each group which is what we want.
The average score on this problem was 94%.
Fill in blank (c).
Answer:
(foo.get('weight') > 20 | foo.get(height) > 40)
Once we have grouped the dogs by 'kind' and have
calculated the average stats of each kind of dog, we can do some
querying with two conditionals: foo.get('weight') > 20
gets the kinds of dogs that are heavier than 20 kg on average and
foo.get('height') > 40) gets the kinds of dogs that are
taller than 40 cm on average. We combine these two conditions with the
| operator since we want the kind of dogs that satisfy
either condition.
The average score on this problem was 93%.
Which of the following should fill in blank (d)?
.index
.unique()
.get('kind')
.get(['kind'])
Answer: .index
Note that earlier, we did groupby('kind'), which
automatically sets each unique 'kind' as the index. Since
this is what we want anyways, simply doing .index will give
us all the kinds of dogs that satisfy the given conditions.
The average score on this problem was 94%.
The following code computes the breed of the cheapest toy dog.
df[__(a)__].__(b)__.__(c)__Fill in part (a).
Answer: df.get('kind') == 'toy'
To find the cheapest toy dog, we can start by narrowing down our
dataframe to only include dogs that are of kind toy. We do this by
constructing the following boolean condition:
df.get('kind') == 'toy', which will check whether a dog is
of kind toy (i.e. whether or not a given row’s 'kind' value
is equal to 'toy'). As a result,
df[df.get('kind') == 'toy'] will retrieve all rows for
which the 'kind' column is equal to 'toy'.
The average score on this problem was 91%.
Fill in part (b).
Answer: .sort_values('price')
Next, we can sort the resulting dataframe by price, which will make
the minimum price (i.e. the cheapest toy dog) easily accessible to us
later on. To sort the dataframe, simply use .sort_values(),
with parameter 'price' as follows:
.sort_values('price')
The average score on this problem was 86%.
Which of the following can fill in blank (c)? Select all that apply.
loc[0]
iloc[0]
index[0]
min()
Answer: index[0]
loc[0]: loc retrieves an element by the
row label, which in this case is by 'breed', not by index
value. Furthermore, loc actually returns the entire row,
which is not what we are looking for. (Note that we are trying to find
the singular 'breed' of the cheapest toy dog.)iloc[0]: While iloc does retrieve elements
by index position, iloc actually returns the entire row,
which is not what we are looking for.index[0]: Note that since 'breed' is the
index column of our dataframe, and since we have already filtered and
sorted the dataframe, simply taking the 'breed' at index 0,
or index[0] will return the 'breed' of the
cheapest toy dog.min(): min() is a method used to find the
smallest value on a series not a dataframe.
The average score on this problem was 81%.
Suppose df is a DataFrame and b is any
boolean array whose length is the same as the number of rows of
df.
True or False: For any such boolean array b,
df[b].shape[0] is less than or equal to
df.shape[0].
True
False
Answer: True
The brackets in df[b] perform a query, or filter, to
keep only the rows of df for which b has a
True entry. Typically, b will come from some
condition, such as the entry in a certain column of df
equaling a certain value. Regardless, df[b] contains a
subset of the rows of df, and .shape[0] counts
the number of rows, so df[b].shape[0] must be less than or
equal to df.shape[0].
The average score on this problem was 86%.
You are given a DataFrame called books that contains
columns 'author' (string), 'title' (string),
'num_chapters' (int), and 'publication_year'
(int).
Suppose that after doing books.groupby('Author').max(),
one row says
| author | title | num_chapters | publication_year |
|---|---|---|---|
| Charles Dickens | Oliver Twist | 53 | 1838 |
Based on this data, can you conclude that Charles Dickens is the alphabetically last of all author names in this dataset?
Yes
No
Answer: No
When we group by 'Author', all books by the same author
get aggregated together into a single row. The aggregation function is
applied separately to each other column besides the column we’re
grouping by. Since we’re grouping by 'Author' here, the
'Author' column never has the max() function
applied to it. Instead, each unique value in the 'Author'
column becomes a value in the index of the grouped DataFrame. We are
told that the Charles Dickens row is just one row of the output, but we
don’t know anything about the other rows of the output, or the other
authors. We can’t say anything about where Charles Dickens falls when
authors are ordered alphabetically (but it’s probably not last!)
The average score on this problem was 94%.
Based on this data, can you conclude that Charles Dickens wrote Oliver Twist?
Yes
No
Answer: Yes
Grouping by 'Author' collapses all books written by the
same author into a single row. Since we’re applying the
max() function to aggregate these books, we can conclude
that Oliver Twist is alphabetically last among all books in the
books DataFrame written by Charles Dickens. So Charles
Dickens did write Oliver Twist based on this data.
The average score on this problem was 95%.
Based on this data, can you conclude that Oliver Twist has 53 chapters?
Yes
No
Answer: No
The key to this problem is that groupby applies the
aggregation function, max() in this case, independently to
each column. The output should be interpreted as follows:
books written by Charles Dickens,
Oliver Twist is the title that is alphabetically last.books written by Charles Dickens, 53
is the greatest number of chapters.books written by Charles Dickens,
1838 is the latest year of publication.However, the book titled Oliver Twist, the book with 53 chapters, and the book published in 1838 are not necessarily all the same book. We cannot conclude, based on this data, that Oliver Twist has 53 chapters.
The average score on this problem was 74%.
Based on this data, can you conclude that Charles Dickens wrote a book with 53 chapters that was published in 1838?
Yes
No
Answer: No
As explained in the previous question, the max()
function is applied separately to each column, so the book written by
Charles Dickens with 53 chapters may not be the same book as the book
written by Charles Dickens published in 1838.
The average score on this problem was 73%.
flights
DataFrame, which details several facts about each of the flights that
King Triton has been on over the past few years. The first few rows of
flights are shown below.
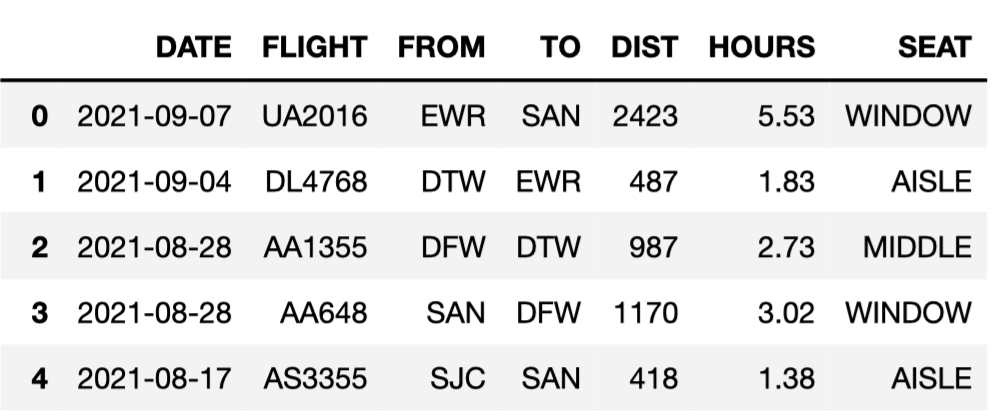
Here’s a description of the columns in flights:
'DATE': the date on which the flight occurred. Assume
that there were no “redeye” flights that spanned multiple days.'FLIGHT': the flight number. Note that this is not
unique; airlines reuse flight numbers on a daily basis.'FROM' and 'TO': the 3-letter airport code
for the departure and arrival airports, respectively. Note that it’s not
possible to have a flight from and to the same airport.'DIST': the distance of the flight, in miles.'HOURS': the length of the flight, in hours.'SEAT': the kind of seat King Triton sat in on the
flight; the only possible values are 'WINDOW',
'MIDDLE', and 'AISLE'. Which of these correctly evaluates to the number of flights King
Triton took to San Diego (airport code 'SAN')?
flights.loc['SAN'].shape[0]
flights[flights.get('TO') == 'SAN'].shape[0]
flights[flights.get('TO') == 'SAN'].shape[1]
len(flights.sort_values('TO', ascending=False).loc['SAN'])
Answer:
flights[flights.get('TO') == 'SAN'].shape[0]
The strategy is to create a DataFrame with only the flights that went
to San Diego, then count the number of rows. The first step is to query
with the condition flights.get('TO') == 'SAN' and the
second step is to extract the number of rows with
.shape[0].
Some of the other answer choices use .loc['SAN'] but
.loc only works with the index, and flights
does not have airport codes in its index.
The average score on this problem was 95%.
Fill in the blanks below so that the result also evaluates to the
number of flights King Triton took to San Diego (airport code
'SAN').
flights.groupby(__(a)__).count().get('FLIGHT').__(b)__ What goes in blank (a)?
'DATE'
'FLIGHT'
'FROM'
'TO'
What goes in blank (b)?
.index[0]
.index[-1]
.loc['SAN']
.iloc['SAN']
.iloc[0]
True or False: If we change .get('FLIGHT') to
.get('SEAT'), the results of the above code block will not
change. (You may assume you answered the previous two subparts
correctly.)
True
False
Answer: 'TO',
.loc['SAN'], True
The strategy here is to group all of King Triton’s flights according
to where they landed, and count up the number that landed in San Diego.
The expression flights.groupby('TO').count() evaluates to a
DataFrame indexed by arrival airport where, for any arrival airport,
each column has a count of the number of King Triton’s flights that
landed at that airport. To get the count for San Diego, we need the
entry in any column for the row corresponding to San Diego. The code
.get('FLIGHT') says we’ll use the 'FLIGHT'
column, but any other column would be equivalent. To access the entry of
this column corresponding to San Diego, we have to use .loc
because we know the name of the value in the index should be
'SAN', but we don’t know the row number or integer
position.
The average score on this problem was 89%.
Consider the DataFrame san, defined below.
san = flights[(flights.get('FROM') == 'SAN') & (flights.get('TO') == 'SAN')]Which of these DataFrames must have the same number
of rows as san?
flights[(flights.get('FROM') == 'SAN') and (flights.get('TO') == 'SAN')]
flights[(flights.get('FROM') == 'SAN') | (flights.get('TO') == 'SAN')]
flights[(flights.get('FROM') == 'LAX') & (flights.get('TO') == 'SAN')]
flights[(flights.get('FROM') == 'LAX') & (flights.get('TO') == 'LAX')]
Answer:
flights[(flights.get('FROM') == 'LAX') & (flights.get('TO') == 'LAX')]
The DataFrame san contains all rows of
flights that have a departure airport of 'SAN'
and an arrival airport of 'SAN'. But as you may know, and
as you’re told in the data description, there are no flights from an
airport to itself. So san is actually an empty DataFrame
with no rows!
We just need to find which of the other DataFrames would necessarily
be empty, and we can see that
flights[(flights.get('FROM') == 'LAX') & (flights.get('TO') == 'LAX')]
will be empty for the same reason.
Note that none of the other answer choices are correct. The first
option uses the Python keyword and instead of the symbol
&, which behaves unexpectedly but does not give an
empty DataFrame. The second option will be non-empty because it will
contain all flights that have San Diego as the departure airport or
arrival airport, and we already know from the first few rows of
flight that there are some of these. The third option will
contain all the flights that King Triton has taken from
'LAX' to 'SAN'. Perhaps he’s never flown this
route, or perhaps he has. This DataFrame could be empty, but it’s not
necessarily going to be empty, as the question requires.
The average score on this problem was 70%.

The DataFrame evs consists of 32 rows,
each of which contains information about a different EV model.
"Brand" (str): The vehicle’s manufacturer."Model" (str): The vehicle’s model name."BodyStyle" (str): The vehicle’s body style."Seats" (int): The vehicle’s number of seats."TopSpeed" (int): The vehicle’s top speed, in
kilometers per hour."Range" (int): The vehicle’s range, or distance it can
travel on a single charge, in kilometers.The first few rows of evs are shown below (though
remember, evs has 32 rows total).

Assume that:
"Brand" column are
"Tesla", "BMW", "Audi", and
"Nissan".import babypandas as bpd and
import numpy as np.Suppose we’ve run the following line of code.
counts = evs.groupby("Brand").count()What value does counts.get("Range").sum() evaluate
to?
Answer: 32
counts is a DataFrame with one row per
"Brand", since we grouped by "Brand". Since we
used the .count() aggregation method, the columns in
counts will all be the same – they will all contain the
number of rows in evs for each "Brand"
(i.e. they will all contain the distribution of "Brand").
If we sum up the values in any one of the columns in
counts, then, the result will be the total number of rows
in evs, which we know to be 32. Thus,
counts.get("Range").sum() is 32.
The average score on this problem was 56%.
What value does counts.index[3] evaluate to?
Answer: "Tesla"
Since we grouped by "Brand" to create
counts, the index of counts will be
"Brand", sorted alphabetically (this sorting happens
automatically when grouping). This means that counts.index
will be the array-like sequence
["Audi", "BMW", "Nissan", "Tesla"], and
counts.index[3] is "Tesla".
The average score on this problem was 33%.
Consider the following incomplete assignment statement.
result = evs______.mean()In each part, fill in the blank above so that result evaluates to the specified quantity.
A DataFrame, indexed by "Brand", whose
"Seats" column contains the average number of
"Seats" per "Brand". (The DataFrame may have
other columns in it as well.)
Answer: .groupby("Brand")
When we group by a column, the resulting DataFrame contains one row
for every unique value in that column. The question specified that we
wanted some information per "Brand", which implies
that grouping by "Brand" is necessary.
After grouping, we need to use an aggregation method. Here, we wanted
the resulting DataFrame to be such that the "Seats" column
contained the average number of "Seats" per
"Brand"; this is accomplished by using
.mean(), which is already done for us.
Note: With the provided solution, the resulting DataFrame also has
other columns. For instance, it has a "Range" column that
contains the average "Range" for each "Brand".
That’s fine, since we were told that the resulting DataFrame may have
other columns in it as well. If we wanted to ensure that the only column
in the resulting DataFrame was "Seats", we could have used
.get(["Brand", "Seats"]) before grouping, though this was
not necessary.
The average score on this problem was 76%.
A number, corresponding to the average "TopSpeed" of all
EVs manufactured by Audi in evs
Answer:
[evs.get("Brand") == "Audi"].get("TopSpeed")
There are two parts to this problem:
Querying, to make sure that we only keep the rows corresponding to Audis. This is accomplished by:
evs.get("Brand") == "Audi" to create a Boolean
Series, with Trues for the rows we want to keep and
Falses for the other rows.True. This is accomplished by
evs[evs.get("Brand") == "Audi"] (though the
evs part at the front was already provided).Accessing the "TopSpeed" column. This is
accomplished by using .get("TopSpeed").
Then, evs[evs.get("Brand") == "Audi"].get("TopSpeed") is
a Series contaning the "TopSpeed"s of all Audis, and mean
of this Series is the result we’re looking for. The call to
.mean() was already provided for us.
The average score on this problem was 77%.

Included is a DataFrame named sungod that contains
information on the artists who have performed at Sun God in years past.
For each year that the festival was held, we have one row for
each artist that performed that year. The columns are:
'Year' (int): the year of the
festival'Artist' (str): the name of the
artist'Appearance_Order' (int): the order in
which the artist appeared in that year’s festival (1 means they came
onstage first)The rows of sungod are arranged in no particular
order. The first few rows of sungod are shown
below (though sungod has many more rows
than pictured here).
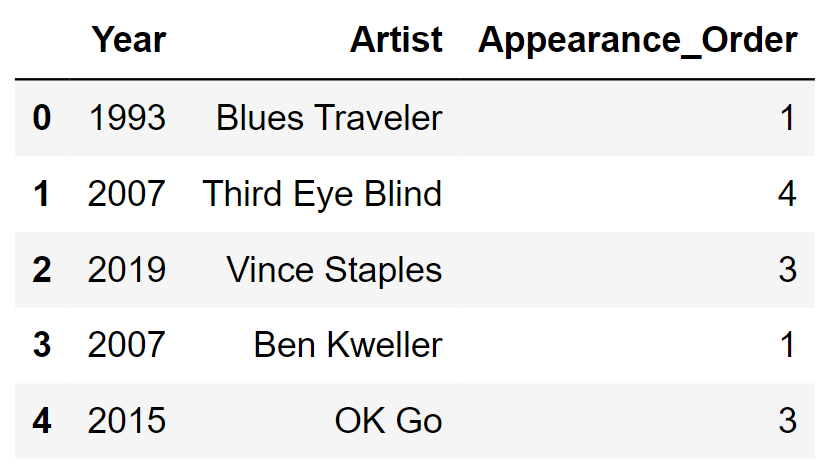
Assume:
Only one artist ever appeared at a time (for example, we can’t
have two separate artists with a 'Year' of 2015 and an
'Appearance_Order' of 3).
An artist may appear in multiple different Sun God festivals (they could be invited back).
We have already run import babypandas as bpd and
import numpy as np.
On the graph paper below, draw the histogram that would be produced by this code.
(
sungod.take(np.arange(5))
.plot(kind='hist', density=True,
bins=np.arange(0, 7, 2), y='Appearance_Order');
)In your drawing, make sure to label the height of each bar in the histogram on the vertical axis. You can scale the axes however you like, and the two axes don’t need to be on the same scale.

Answer:
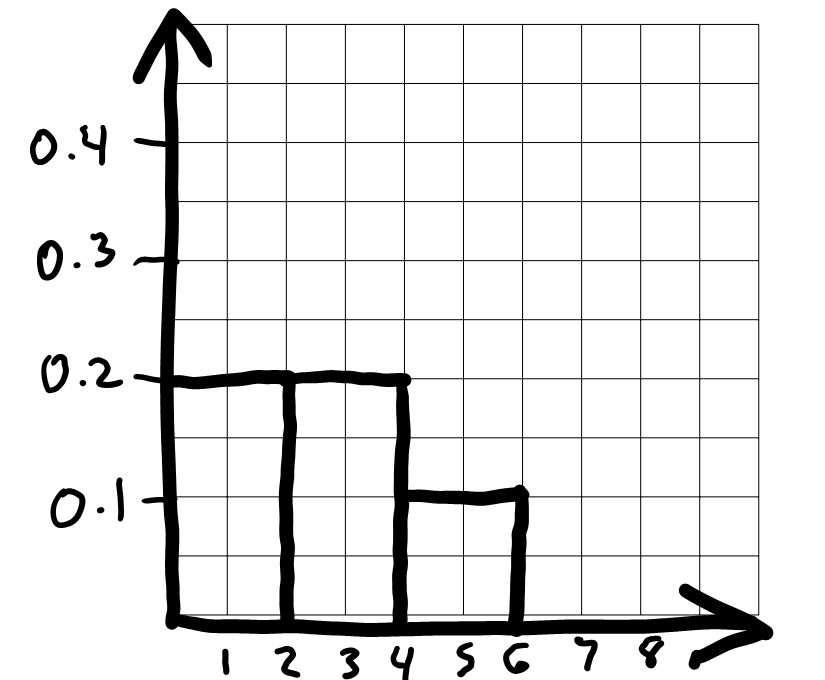
To draw the histogram, we first need to bin the data and figure out
how many data values fall into each bin. The code includes
bins=np.arange(0, 7, 2) which means the bin endpoints are
0, 2, 4, 6. This gives us three bins:
[0, 2), [2,
4), and [4, 6]. Remember that
all bins, except for the last one, include the left endpoint but not the
right. The last bin includes both endpoints.
Now that we know what the bins are, we can count up the number of
values in each bin. We need to look at the
'Appearance_Order' column of
sungod.take(np.arange(5)), or the first five rows of
sungod. The values there are 1,
4, 3, 1, 3. The two 1s fall into
the first bin [0, 2). The two 3s fall into the second bin [2, 4), and the one 4 falls into the last bin [4, 6]. This means the proportion of values
in each bin are \frac{2}{5}, \frac{2}{5},
\frac{1}{5} from left to right.
To figure out the height of each bar in the histogram, we use the fact that the area of a bar in a density histogram should equal the proportion of values in that bin. The area of a rectangle is height times width, so height is area divided by width.
For the bin [0, 2), the area is \frac{2}{5} = 0.4 and the width is 2, so the height is \frac{0.4}{2} = 0.2.
For the bin [2, 4), the area is \frac{2}{5} = 0.4 and the width is 2, so the height is \frac{0.4}{2} = 0.2.
For the bin [4, 6], the area is \frac{1}{5} = 0.2 and the width is 2, so the height is \frac{0.2}{2} = 0.1.
Since the bins are all the same width, the fact that there an equal number of values in the first two bins and half as many in the third bin means the first two bars should be equally tall and the third should be half as tall. We can use this to draw the rest of the histogram quickly once we’ve drawn the first bar.
The average score on this problem was 45%.
You have a DataFrame called prices that contains
information about food prices at 18 different grocery stores. There is
column called 'broccoli' that contains the price in dollars
for one pound of broccoli at each grocery store. There is also a column
called 'ice_cream' that contains the price in dollars for a
pint of store-brand ice cream.
Using the code,
prices.plot(kind='hist', y='broccoli', bins=np.arange(0.8, 2.11, 0.1), density=True)we produced the histogram below:
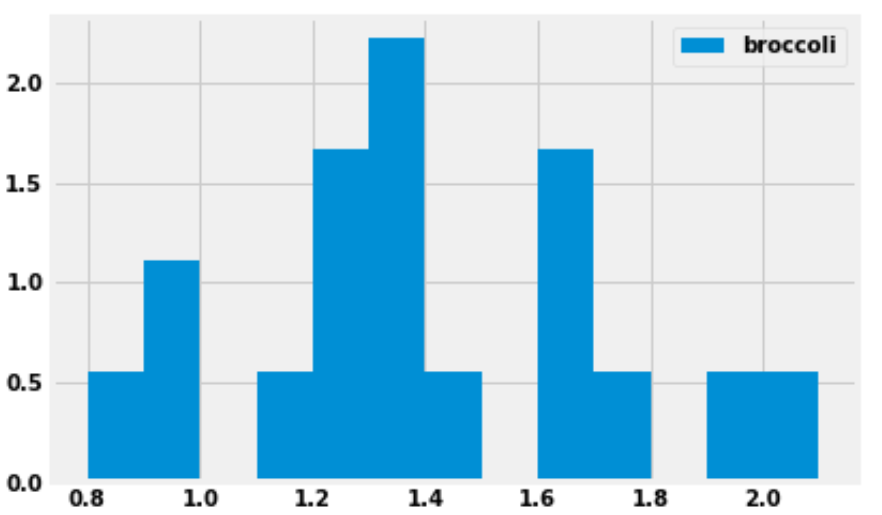
How many grocery stores sold broccoli for a price greater than or equal to $1.30 per pound, but less than $1.40 per pound (the tallest bar)?
Answer: 4 grocery stores
We are given that the bins start at 0.8 and have a width of 0.1, which means one of the bins has endpoints 1.3 and 1.4. This bin (the tallest bar) includes all grocery stores that sold broccoli for a price greater than or equal to $1.30 per pound, but less than $1.40 per pound.
This bar has a width of 0.1 and we’d estimate the height to be around 2.2, though we can’t say exactly. Multiplying these values, the area of the bar is about 0.22, which means about 22 percent of the grocery stores fall into this bin. There are 18 grocery stores in total, as we are told in the introduction to this question. We can compute using a calculator that 22 percent of 18 is 3.96. Since the actual number of grocery stores this represents must be a whole number, this bin must represent 4 grocery stores.
The reason for the slight discrepancy between 3.96 and 4 is that we used 2.2 for the height of the bar, a number that we determined by eye. We don’t know the exact height of the bar. It is reassuring to do the calculation and get a value that’s very close to an integer, since we know the final answer must be an integer.
The average score on this problem was 71%.
Suppose we now plot the same data with different bins, using the following line of code:
prices.plot(kind='hist', y='broccoli', bins=[0.8, 1, 1.1, 1.5, 1.8, 1.9, 2.5], density=True)What would be the height on the y-axis for the bin corresponding to the interval [\$1.10, \$1.50)? Input your answer below.
Answer: 1.25
First, we need to figure out how many grocery stores the bin [\$1.10, \$1.50) contains. We already know from the previous subpart that there are four grocery stores in the bin [\$1.30, \$1.40). We could do similar calculations to find the number of grocery stores in each of these bins:
However, it’s much simpler and faster to use the fact that when the bins are all equally wide, the height of a bar is proportional to the number of data values it contains. So looking at the histogram in the previous subpart, since we know the [\$1.30, \$1.40) bin contains 4 grocery stores, then the [\$1.10, \$1.20) bin must contain 1 grocery store, since it’s only a quarter as tall. Again, we’re taking advantage of the fact that there must be an integer number of grocery stores in each bin when we say it’s 1/4 as tall. Our only options are 1/4, 1/2, or 3/4 as tall, and among those choices, it’s clear.
Therefore, by looking at the relative heights of the bars, we can quickly determine the number of grocery stores in each bin:
Adding these numbers together, this means there are 9 grocery stores whose broccoli prices fall in the interval [\$1.10, \$1.50). In the new histogram, these 9 grocery stores will be represented by a bar of width 1.50-1.10 = 0.4. The area of the bar should be \frac{9}{18} = 0.5. Therefore the height must be \frac{0.5}{0.4} = 1.25.
The average score on this problem was 33%.
You are interested in finding out the number of stores in which a pint of ice cream was cheaper than a pound of broccoli. Will you be able to determine the answer to this question by looking at the plot produced by the code below?
prices.get(['broccoli', 'ice_cream']).plot(kind='barh')Yes
No
Answer: Yes
When we use .plot without specifying a y
column, it uses every column in the DataFrame as a y column
and creates an overlaid plot. Since we first use get with
the list ['broccoli', 'ice_cream'], this keeps the
'broccoli' and 'ice_cream' columns from
prices, so our bar chart will overlay broccoli prices with
ice cream prices. Notice that this get is unnecessary
because prices only has these two columns, so it would have
been the same to just use prices directly. The resulting
bar chart will look something like this:
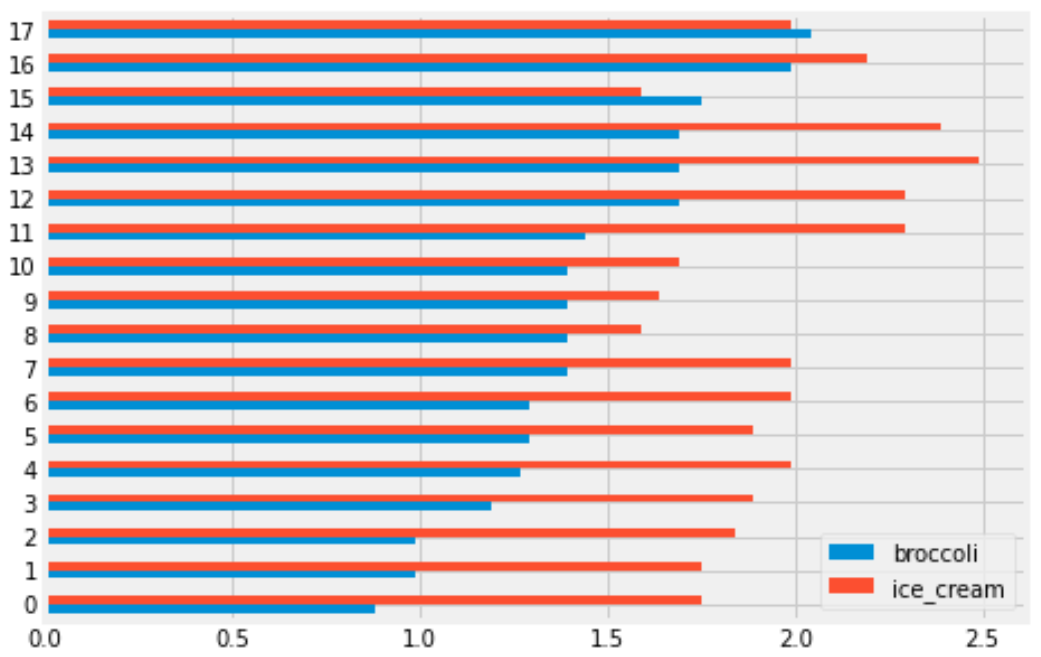
Each grocery store has its broccoli price represented by the length of the blue bar and its ice cream price represented by the length of the red bar. We can therefore answer the question by simply counting the number of red bars that are shorter than their corresponding blue bars.
The average score on this problem was 78%.
You are interested in finding out the number of stores in which a pint of ice cream was cheaper than a pound of broccoli. Will you be able to determine the answer to this question by looking at the plot produced by the code below?
prices.get(['broccoli', 'ice_cream']).plot(kind='hist')Yes
No
Answer: No
This will create an overlaid histogram of broccoli prices and ice cream prices. So we will be able to see the distribution of broccoli prices together with the distribution of ice cream prices, but we won’t be able to pair up particular broccoli prices with ice cream prices at the same store. This means we won’t be able to answer the question. The overlaid histogram would look something like this:
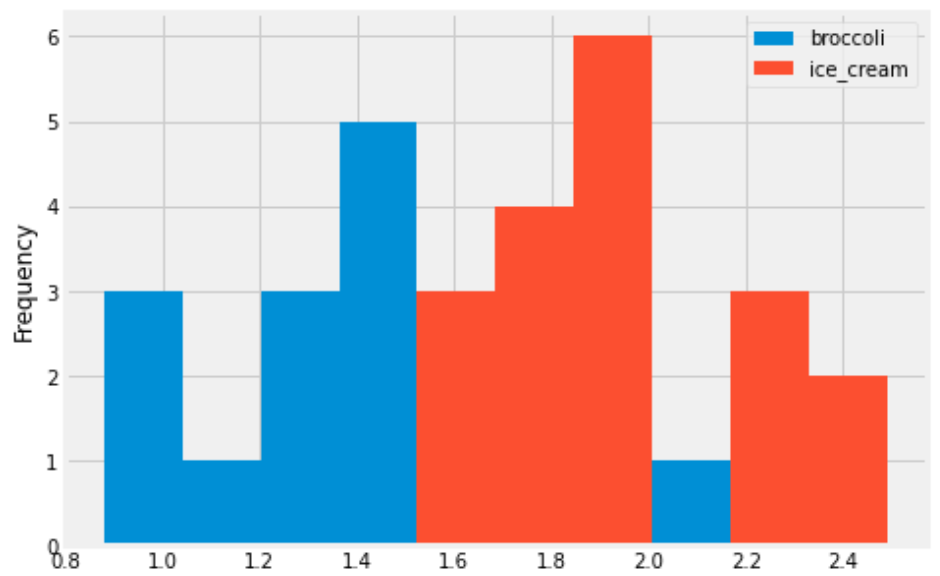
This tells us that broadly, ice cream tends to be more expensive than broccoli, but we can’t say anything about the number of stores where ice cream is cheaper than broccoli.
The average score on this problem was 81%.
Some code and the scatterplot that produced it is shown below:
(prices.get(['broccoli', 'ice_cream']).plot(kind='scatter', x='broccoli', y='ice_cream'))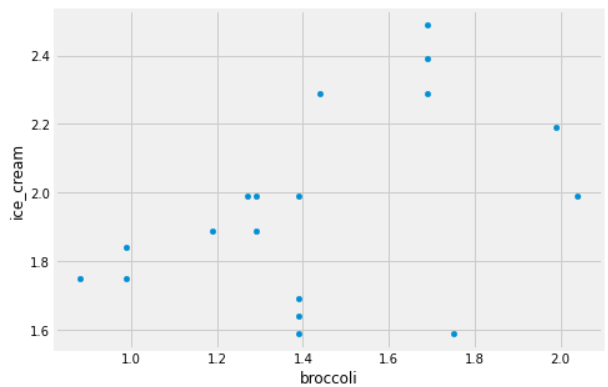
Can you use this plot to figure out the number of stores in which a pint of ice cream was cheaper than a pound of broccoli?
If so, say how many such stores there are and explain how you came to that conclusion.
If not, explain why this scatterplot cannot be used to answer the question.
Answer: Yes, and there are 2 such stores.
In this scatterplot, each grocery store is represented as one dot. The x-coordinate of that dot tells the price of broccoli at that store, and the y-coordinate tells the price of ice cream. If a grocery store’s ice cream price is cheaper than its broccoli price, the dot in the scatterplot will have y<x. To identify such dots in the scatterplot, imagine drawing the line y=x. Any dot below this line corresponds to a point with y<x, which is a grocery store where ice cream is cheaper than broccoli. As we can see, there are two such stores.
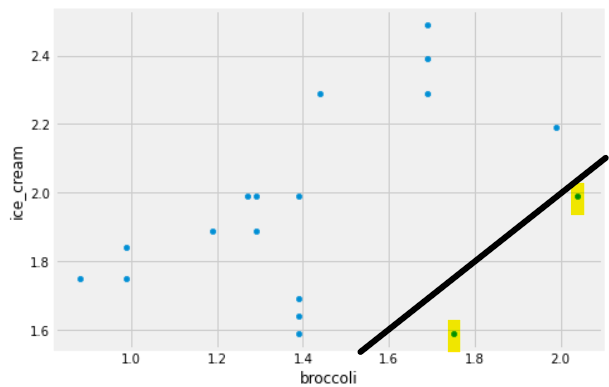
The average score on this problem was 78%.
Nintendo collected data on the heights of a sample of Animal Crossing: New Horizons players. A histogram of the heights in their sample is given below.
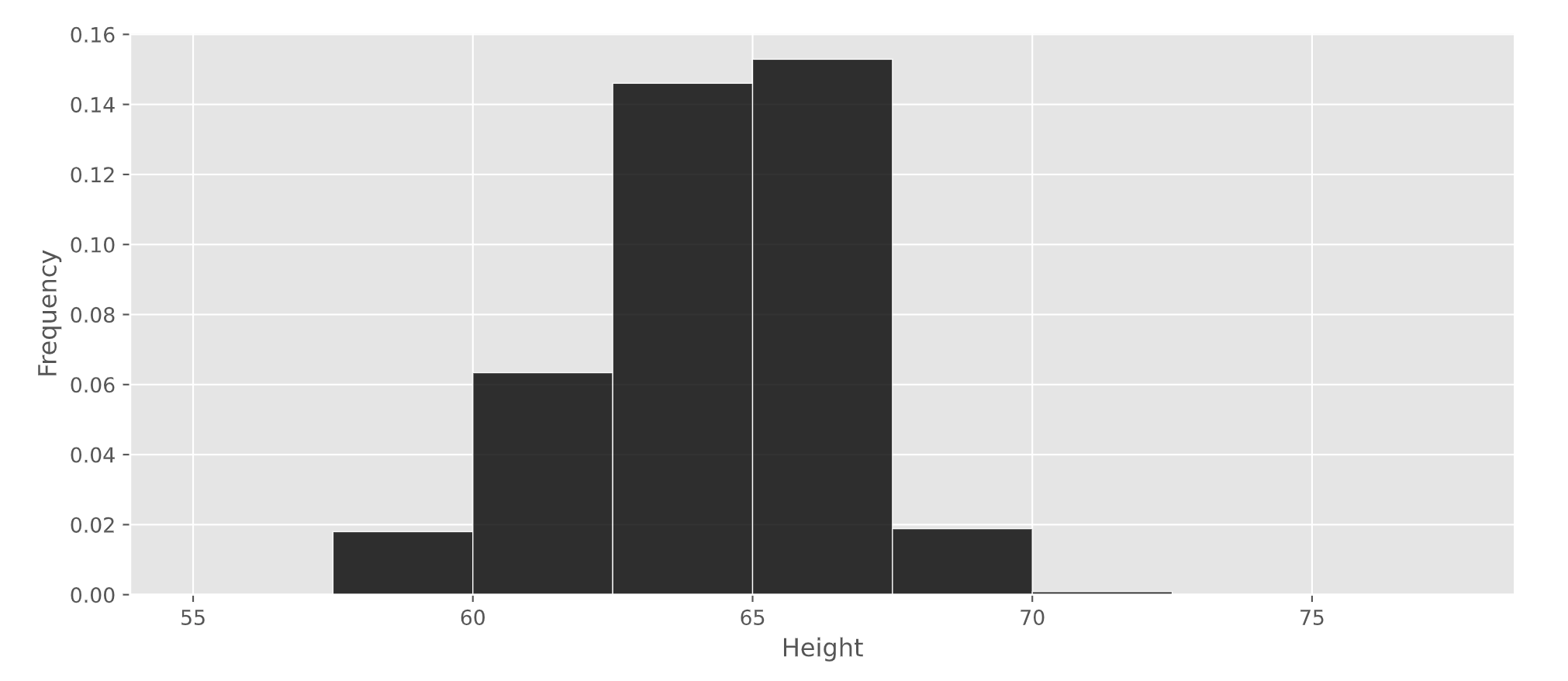
What percentage of players in Nintendo’s sample are at least 62.5 inches tall? Give your answer as an integer rounded to the nearest multiple of 5.
Answer: 80%
The average score on this problem was 73%.
You are given a DataFrame called restaurants that
contains information on a variety of local restaurants’ daily number of
customers and daily income. There is a row for each restaurant for each
date in a given five-year time period.
The columns of restaurants are 'name'
(string), 'year' (int), 'month' (int),
'day' (int), 'num_diners' (int), and
'income' (float).
Assume that in our data set, there are not two different restaurants
that go by the same 'name' (chain restaurants, for
example).
What type of visualization would be best to display the data in a way that helps to answer the question “Do more customers bring in more income?”
scatterplot
line plot
bar chart
histogram
Answer: scatterplot
The number of customers is given by 'num_diners' which
is an integer, and 'income' is a float. Since both are
numerical variables, neither of which represents time, it is most
appropriate to use a scatterplot.
The average score on this problem was 87%.
What type of visualization would be best to display the data in a way that helps to answer the question “Have restaurants’ daily incomes been declining over time?”
scatterplot
line plot
bar chart
histogram
Answer: line plot
Since we want to plot a trend of a numerical quantity
('income') over time, it is best to use a line plot.
The average score on this problem was 95%.
Suppose there are 200 students enrolled in DSC 10, and that the histogram below displays the distribution of the number of Instagram followers each student has, measured in 100s. That is, if a student is represented in the first bin, they have between 0 and 200 Instagram followers.
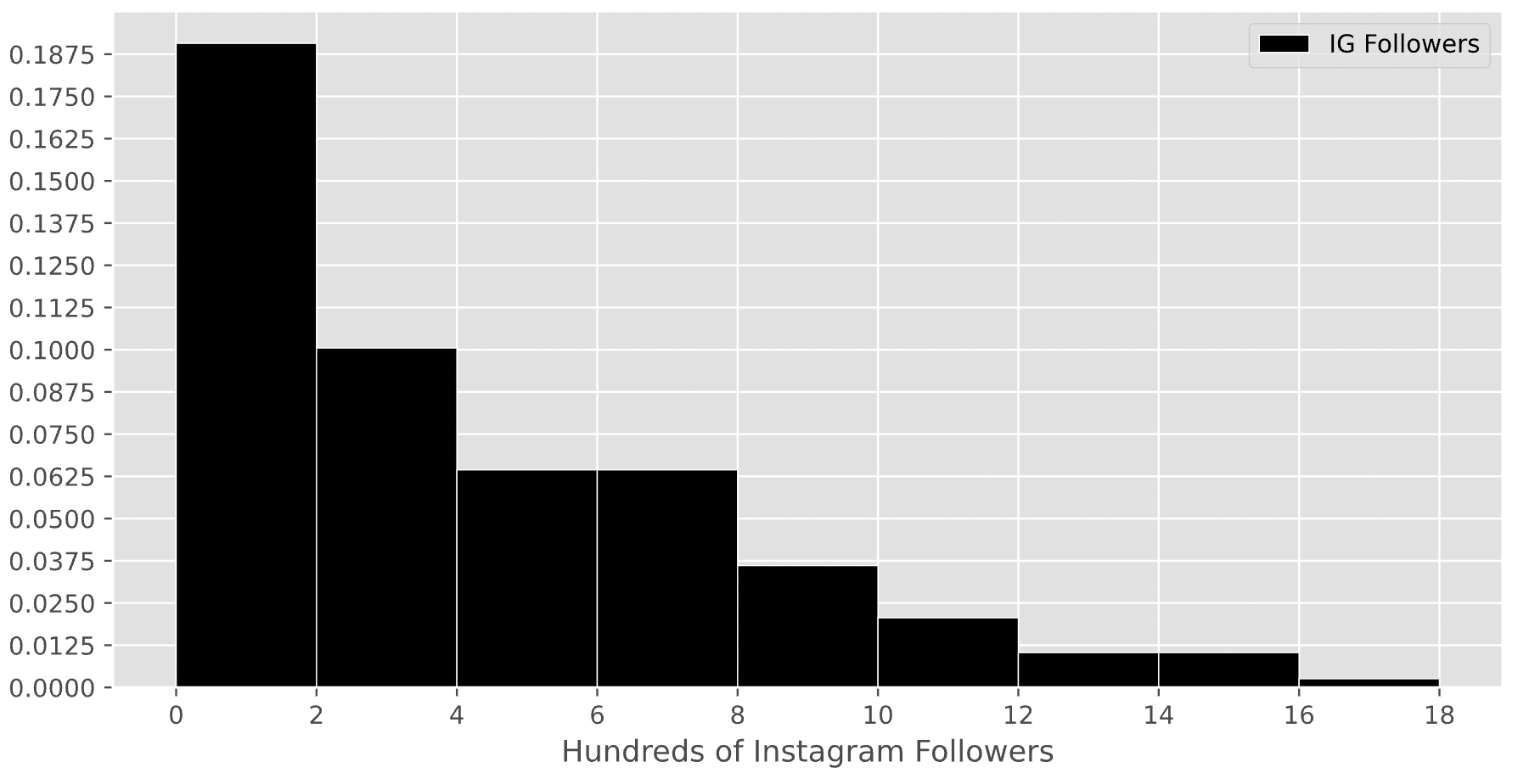
How many students in DSC 10 have between 200 and 800 Instagram followers? Give your answer as an integer.
Answer: 90
Remember, the key property of histograms is that the proportion of values in a bin is equal to the area of the corresponding bar. To find the number of values in the range 2-8 (the x-axis is measured in hundreds), we’ll need to find the proportion of values in the range 2-8 and multiply that by 200, which is the total number of students in DSC 10. To find the proportion of values in the range 2-8, we’ll need to find the areas of the 2-4, 4-6, and 6-8 bars.
Area of the 2-4 bar: \text{width} \cdot \text{height} = 2 \cdot 0.1 = 0.2
Area of the 4-6 bar: \text{width} \cdot \text{height} = 2 \cdot 0.0625 = 0.125.
Area of the 6-8 bar: \text{width} \cdot \text{height} = 2 \cdot 0.0625 = 0.125.
Then, the total proportion of values in the range 2-8 is 0.2 + 0.125 + 0.125 = 0.45, so the total number of students with between 200 and 800 Instagram followers is 0.45 \cdot 200 = 90.
The average score on this problem was 49%.
Suppose the height of a bar in the above histogram is h. How many students are represented in the corresponding bin, in terms of h?
Hint: Just as in the first subpart, you’ll need to use the assumption from the start of the problem.
20 \cdot h
100 \cdot h
200 \cdot h
400 \cdot h
800 \cdot h
Answer: 400 \cdot h
As we said at the start of the last solution, the key property of histograms is that the proportion of values in a bin is equal to the area of the corresponding bar. Then, the number of students represented bar a bar is the total number of students in DSC 10 (200) multiplied by the area of the bar.
Since all bars in this histogram have a width of 2, the area of a bar in this histogram is \text{width} \cdot \text{height} = 2 \cdot h. If there are 200 students in total, then the number of students represented in a bar with height h is 200 \cdot 2 \cdot h = 400 \cdot h.
To verify our answer, we can check to see if it makes sense in the context of the previous subpart. The 2-4 bin has a height of 0.1, and 400 \cdot 0.1 = 40. The total number of students in the range 2-8 was 90, so it makes sense that 40 of them came from the 2-4 bar, since the 2-4 bar takes up about half of the area of the 2-8 range.
The average score on this problem was 36%.