← return to practice.dsc10.com
Instructor(s): Janine Tiefenbruck
This exam was administered in-person. The exam was closed-notes, except students were allowed to bring their own double-sided cheat sheet. No calculators were allowed. Students had 50 minutes to take this exam.
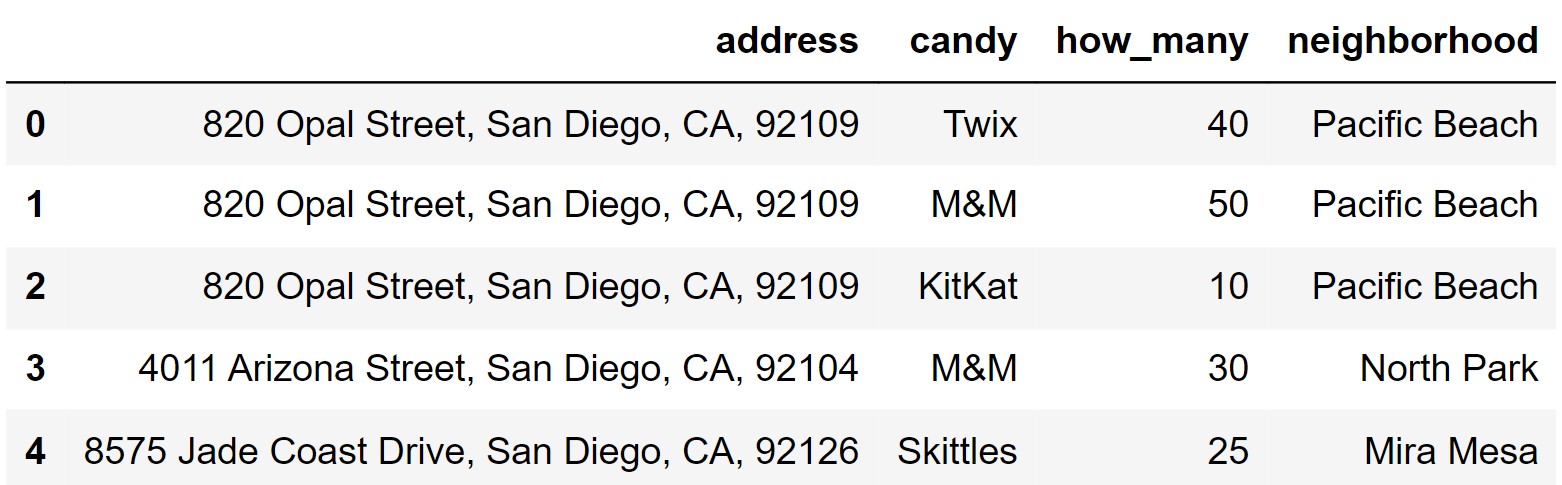
Trick-or-treating is a Halloween tradition, where children wear costumes and walk around their neighborhood from house to house to collect candy. In this exam, you’ll work with a data set representing the candy given out on Halloween. Each row represents one type of candy given out by one house in San Diego.
The columns of treat are as follows:
"address" (str): The address of the house
giving out candy."candy" (str): The type of candy that is
being given out."how_many" (int): How many pieces of candy
are being given out."neighborhood" (str): The neighborhood
that the house is in.The first few rows of treat are shown below, though
treat has many more rows than pictured.

Throughout this exam, we will refer to treat repeatedly.
Assume that we have already run import babypandas as bpd
and import numpy as np.
Which of the following columns would be an appropriate index for the
treat DataFrame?
"address"
"candy"
"neighborhood"
None of these.
Answer: None of these.
The index uniquely identifies each row of a DataFrame. As a result,
for a column to be a candidate for the index, it must not contain repeat
items. Since it is possible for an address to give out different types
of candy, values in "address" can show up multiple times.
Similarly, values in "candy" can also show up multiple
times as it will appear anytime a house gives it out. Finally, a
neighborhood has multiple houses, so if more than one of those houses
show up, that value in "neighborhood" will appear multiple
times. Since "address", "candy", and
"neighborhood" can potentially have repeat values, none of
them can be the index for treat.
The average score on this problem was 54%.
Which of the following expressions evaluate to
"M&M"? Select all that apply.
treat.get("candy").iloc[1]
treat.sort_values(by="candy", ascending = False).get("candy").iloc[1]
treat.sort_values(by="candy", ascending = False).get("candy").loc[1]
treat.set_index("candy").index[-1]
None of these.
Answer: treat.get("candy").iloc[1] and
treat.sort_values(by="candy", ascending = False).get("candy").loc[1]
Option 1:
treat.get("candy").iloc[1] gets the candy
column and then retrieves the value at index location 1,
which would be "M&M".
Option 2:
treat.sort_values(by="candy", ascending=False).get("candy").iloc[1]
sorts the candy column in descending order (alphabetically,
the last candy is at the top) and then retrieves the value at index
location 1 in the candy column. The entire
dataset is not shown, but in the given rows, the second-to-last candy
alphabetically is "Skittles", so we know that
"M&M" will not be the second-to-last alphabetical candy
in the full dataset.
Option 3:
treat.sort_values(by="candy", ascending=False).get("candy").loc[1]
is very similar to the last option; however, this time,
.loc[1] is used instead of .iloc[1]. This
means that instead of looking at the row in position 1
(second row) of the sorted DataFrame, we are finding the row with an
index label of 1. When the rows are sorted by
candy in descending order, the index labels remain with
their original rows, so the "M&M" row is retrieved when
we search for the index label 1.
Option 4:
treat.set_index("candy").index[-1] sets the index to the
candy column and then retrieves the last element in the
index (candy). The entire dataset is not shown, but in the
given rows, the last value would be "Skittles" and not
"M&M". The last value of the full dataset could be
"M&M", but since we are not sure, this option is not
selected.
The average score on this problem was 66%.
Consider the code below.
street = treats.get("address").str.contains("Street")
sour = treats.get("candy").str.contains("Sour")What is the data type of street?
int
bool
str
Series
DataFrame
Answer: Series
.str.contains works in a series and returns a series of booleans.
Each entry is True if it contains a certain string or
False otherwise. So the answer is street has
the Series data type.
The average score on this problem was 75%.
What does the following expression evaluate to? Write your answer exactly how the output would appear in Python.
np.count_nonzero(street & sour) > sour.sum()Answer: False
np.count_nonzero(street & sour) counts the number of
rows that contains the word “Street” in the address column
AND also contains the word “Sour” in candy.
sour.sum() sums up all the trues and falses, effectively
making it a count of rows that contain the word “Sour” in
candy. Even if we don’t know the full dataframe, we should
be able to figure out that the number of rows that satisfy the condition
of both Street AND Sour should be lower than
or equal to the number of rows that satisfy Sour by itself.
Therefore, it’s impossible for
np.count_nonzero(street & sour) > sour.sum() to be
True so the answer is False.
The average score on this problem was 59%.
The "address" column contains quite a bit of
information. All houses are in "San Diego, CA", but the
street address and the zip code vary. Note that the “street address"
includes both the house number and street name, such as
"820 Opal Street". All addresses are formatted in the same
way, for example,
"820 Opal Street, San Diego, CA, 92109".
Fill in the blanks in the function address_part below.
The function has two inputs: a value in the index of treat
and a string part, which is either "street" or
"zip". The function should return the appropriate part of
the address at the given index value, as a string. Example behavior is
given below.
>>> address_part(4, "street")
"8575 Jade Coast Drive"
>>> address_part(1, "zip")
"92109"The function already has a return statement included. You should not
add the word return anywhere else!
def address_part(index_value, part):
if part == "street":
var = 0
else:
___(a)___
return treat.get("address").loc[___(b)___].___(c)___Answer:
(a): var = 3, var = -1 or alternate
solution var = 1
(b): index_value
(c): split(", ")[var] or alternate solution
split(", San Diego, CA, ")[var]
The average score on this problem was 58%.
Suppose we had a different function called zip_as_int
that took as input a single address, formatted exactly as the addresses
in treat, and returned the zip code as an int.
Write a Python expression using the zip_as_int function
that evaluates to a Series with the zip codes of all the addresses in
treat.
Answer:
treat.get("address").apply(zip_as_int)
The average score on this problem was 76%.
Write a Python expression that evaluates to the address of the house with the most pieces of candy available (the most pieces, not the most varieties).
It’s okay if you need to write on multiple lines, but your code should represent a single expression in Python.
Answer:
treat.groupby("address").sum().sort_values(by="how_many", ascending = False).index[0]
or
treat.groupby("addresss").sum().sort_values(by="how_many").index[-1]
In the treat DataFrame, there are multiple rows for each
address, one for each candy they are giving out with their quantity.
Since we want the address with the most pieces of candy available, we
need to combine this information, so we start by grouping by address:
treat.groupby(“address”). Now, since we want to add the
number of candy available per address, we use the sum()
aggregate function. So now we have a DataFrame with one row per address
where there value in each column is the sum of all the values. To get
the address with the most pieces of candy available, we can simply sort
by the “how_many” column since this stores the total amount
of candy per house. Setting ascending=False means that the
address with the greatest amount of candy will be the first row. Since
the addresses are located in the index as a result of the
groupby, we can access this value by using
index[0].
Note: If you do not set ascending=False, then the
address with the most amount of candy available will be the last row
which you can access by index[-1].
The average score on this problem was 67%.
Suppose you visit a house that has 40 Twix, 50 M&Ms, and 10 KitKats in a bowl. You take three pieces of candy from this bowl.
What is the probability you get all Twix?
\dfrac{40}{100} \cdot \dfrac{39}{100} \cdot \dfrac{38}{100}
\dfrac{40}{100} \cdot \dfrac{40}{99} \cdot \dfrac{40}{98}
\dfrac{40}{100} \cdot \dfrac{40}{100} \cdot \dfrac{40}{100}
\dfrac{40}{100} \cdot \dfrac{39}{99} \cdot \dfrac{38}{98}
Answer: \dfrac{40}{100} \cdot \dfrac{39}{99} \cdot \dfrac{38}{98}
We need to find the probability that we get all Twix among the three candies selected from the bowl. Since we are selecting three times from the same bowl, we know that we are selecting without replacement.
The total probability that we grab all Twix from the bowl is the product of these probabilities: \frac{40}{100} \cdot \frac{39}{99} \cdot \frac{38}{98}
The average score on this problem was 94%.
What is the probability you get no Twix? Leave your answer completely unsimplified, similar to the answer choices for part (a).
Answer: \dfrac{60}{100} \cdot \dfrac{59}{99} \cdot \dfrac{58}{98}
We need to find the probability that we get no Twix among the three candies selected from the bowl. We know that two candies are not Twix in our bowl (M&Ms and Kitkats). Since we are selecting three times from the same bowl, we know that we are selecting without replacement.
The total probability that we grab no Twix from the bowl is the product of these probabilities: \frac{60}{100} \cdot \frac{59}{99} \cdot \frac{58}{98}
The average score on this problem was 81%.
Let a be your answer to part (a) and let b be your answer to part (b). Write a mathematical expression in terms of a and/or b that evaluates to the probability of getting some Twix and some non-Twix candy from this house.
Answer: 1 - a - b or 1 - (a + b)
The case where we get some Twix and some non-Twix occurs can also be thought of as the case when we DO NOT get either all Twix OR all non-Twix. In 6.1 we calculated the probability of getting all Twix as a and in 6.2 we calculated the probability of getting all non-Twix as b. Therefore the probability of getting either all Twix OR all non-Twix is equal to a + b. However, we are looking for the probability that this does not happen, meaning our answer is 1 - (a + b).
The average score on this problem was 30%.
Suppose you visit another house and their candy bowl is composed of 2 Twix, 3 Rolos, 1 Snickers, 3 M&Ms, and 1 KitKat. You do the same as before and take 3 candies from the bowl at random.
Fill in the blanks in the code below so that
prob_all_same evaluates to an estimate of the probability
that you get three of the same type of candy.
candy_bowl = np.array(["Twix", "Twix", "Rolo", "Rolo", "Rolo", "Snickers", "M&M", "M&M", "M&M", "KitKat"])
repetitions = 10000
prob_all_same = 0
for i in np.arange(repetitions):
grab = np.random.choice(___(a)___)
if ___(b)___:
prob_all_same = prob_all_same + 1
prob_all_same = ___(c)___What goes in blank (a)?
candy_bowl, len(candy_bowl), replace=False
candy_bowl, 3, replace=False
candy_bowl, 3, replace=True
candy_bowl, repetitions, replace=True
Answer:
candy_bowl, 3, replace=False
The question asks us to “take 3 candies from the bowl at random.” In
this part, we need to sample 3 candies at random using
np.random.choice. Now, we evaluate each option one by one
as follows:
candy_bowl, len(candy_bowl), replace=False: The code
tries to sample all candies without replacement. However, we are asked
to only sample three candies, not all.
candy_bowl, 3, replace=False: The code samples three
candies without replacement, which matches the description. This option
is correct.
candy_bowl, 3, replace=True: The code samples three
candies from the bowl with replacement. Under this setting, the same
candy can be selected multiple times in a single grab, which is not
realistic.
candy_bowl, repetitions, replace=True: This option
attempts to sample repetitions (10,000) candies in a single
grab. We are asked to sample three candies per iteration of the loop,
not thousands.
The average score on this problem was 88%.
What goes in blank (b)?
grab[0] == "Rolo" and grab[1] == "Rolo" and grab[2] == "Rolo"
grab[0] == grab[1] and grab[0] == grab[2]
grab[0] == grab[1] or grab[0] == grab[2]
grab == "Rolo" | grab == "M&M"
Answer:
grab[0] == grab[1] and grab[0] == grab[2]
Here, we need condition that checks if all three candies selected in the grab are the same. We now analyze each option as follows:
grab[0] == "Rolo" and grab[1] == "Rolo" and grab[2] == "Rolo":
This condition explicitly checks if all three candies are “Rolo”. While
it ensures that the three candies are the same, it only works for “Rolo”
and not for other types of candy in the bowl (e.g., “Twix,”
“M&M”).
grab[0] == grab[1] and grab[0] == grab[2]: This
condition checks if the first candy (grab[0]) is the same as the second
(grab[1]) and the third (grab[2]). If all three candies are the same
type (regardless of which type), this condition will evaluate to True.
Otherwise, the expression will evaluate to False, which is what we need.
The option is correct.
grab[0] == grab[1] or grab[0] == grab[2]: This
condition checks if the first candy (grab[0]) matches either the second
(grab[1]) or the third (grab[2]). It does not require all three candies
to be the same. For example, if grab = [“Twix”, “Twix”, “M&M”], this
condition would incorrectly evaluate to True.
grab == "Rolo" | grab == "M&M": This condition
is syntactically invalid. It tries to compare the grab list (which
contains three elements) with two strings (“Rolo” and “M&M”) using a
bitwise OR (|), not to mention that it does not check if three candies
are the same.
The average score on this problem was 92%.
What goes in blank (c)?
prob_all_same.mean()
prob_all_same / len(candy_bowl)
prob_all_same / repetitions
prob_all_same / 3
Answer: prob_all_same / repetitions
To calculate the estimated probability of drawing three candies of
the same type, we divide the total number of successes
(prob_all_same, which counts the instances where all three
candies are identical) by the total number of iterations
(repetitions).
The option prob_all_same.mean() is incorrect because
prob_all_same is an integer that accumulates the count of
successful trials, not an array or list that supports the
.mean() method. Similarly, dividing by
len(candy_bowl) or 3 is incorrect, as neither
represents the total number of iterations. Therefore, using these values
as the denominator would not provide an accurate probability
estimate.
The average score on this problem was 86%.
Select the correct way to fill in the blank such that the code below
evaluates to True.
treat.groupby(______).mean().shape[0] == treat.shape[0] "address"
"candy"
"neighborhood"
["address", "candy"]
["candy", "neighborhood"]
["address", "neighborhood"]
Answer: ["address", "candy"]
.shape returns a tuple containing the number of rows and
number of columns of a DataFrame respectively. By indexing
.shape[0] we get the number of rows. In the above question,
we are comparing whether the number of rows of treat
grouped by its column(s) is equal to the number of rows of the original
treat itself. This is only possible when there is a unique
row for each value in the column or for each combination of columns.
Since it is possible for an address to give out different types of
candy, values in "address" can show up multiple times.
Similarly, values in "candy" can also show up multiple
times since more than one house may give out a specific candy. A
neighborhood has multiple houses, so if a neighborhood has more than one
house, "neighborhood" will appear multiple times.
% write for combinations here % Each address gives out a specific
candy only once, and hence ["address", "candy"] would have
a unique row for each combination. This would make the number of rows in
the grouped DataFrame equal to treat itself. Multiple
neighborhoods might be giving out the same candy or a single
neighborhood could be giving out multiple candies, so
["candy", "neighborhood"] is not the answer. Finally, a
neighborhood can have multiple addresses, but each address could be
giving out more than one candy, which would mean this combination would
occur multiple times in treat, which means this would also
not be an answer. Since ["address", "candy"] is the only
combination that gives a unique row for each combination, the grouped
DataFrame would contain the same number of rows as treat
itself.
The average score on this problem was 69%.
Assume that all houses in treat give out the same size
candy, say fun-sized. Suppose we have an additional DataFrame,
trick, which is indexed by "candy" and has one
column, "price", containing the cost in dollars of a
single piece of fun-sized candy, as a
float.
Suppose that:
treat has 200 rows total, and includes 15 distinct
types of candies.
trick has 25 rows total: 15 for the candies that
appear in treat, plus 10 additional rows that correspond to
candies not represented in treat.
Consider the following line of code:
trick_or_treat = trick.merge(treat, left_index = True, right_on = "candy")How many rows does trick_or_treat have?
15
25
200
215
225
3000
5000
Answer: 200
We are told that trick has 25 rows: 15 from candies that
are in treat and 10 additional candies. This means that
each candy in trick appears exactly once because 15+10= 25.
In addition, a general property when merging dataframes is that the
number of rows for one shared value between the dataframes is the
product of the number of occurences in either dataframe. For example, if
Twix occurs 5 times in treat, the number of times it occurs
in trick_or_treat is 5 * 1 = 5 (it occurs once in
trick). Using this logic, we can determine how many rows
are in trick_or_treat. Since each number of candies is
multipled by one and they sum up to 200, the number of rows will be
200.
The average score on this problem was 39%.
Recall from the last problem that the DataFrame
trick_or_treat includes a column called
"price" with the cost in dollars of a single
piece of fun-sized candy, as a float.
Assume we have run the line of code tot = trick_or_treat
to reassign trick_or_treat to the shorter variable name
tot.
In this problem, we’ll use tot to calculate the total
amount of money that each house spent on Halloween candy. This number is
always less than \$80 for the houses in
our data set.
Fill in the blanks below so that the following block of code plots a histogram that displays the distribution of the total amount of money that houses spent on Halloween candy, in dollars.
total = (tot.assign(total_spent = ___(a)___)
.groupby(___(b)___).___(c)___)
total.plot(kind = "hist", y = "total_spent", density = True,
bins = np.arange(0, 90, 10))
Answer:
(a): tot.get("price") * tot.get("how_many")
(b): “address”
(c): sum()
(a):
tot.get("price") * tot.get("how_many")
tot.get("price") retrieves the cost of a single piece
of candy.tot.get("how_many") retrieves the number of pieces of
candy given out.total_spent that
represents the total money spent for each type of candy at a given
house.(b): “address”
"address" column, which
uniquely identifies each house. This ensures that all records associated
with a single house are aggregated together.(c): sum()
"address", the .sum()
operation aggregates the total amount of money spent on candy for each
house. This sums up all total_spent values for records
belonging to the same house.Final Output: The total DataFrame will have one row for
each house, with the column total_spent representing the
total money spent on Halloween candy. Finally, the
total.plot command creates a histogram of the
total_spent values to visualize the distribution of
spending across houses.
The average score on this problem was 65%.
The histogram below displays the distribution of the total amount of money that houses spent on Halloween candy; it is the histogram that would be generated from the code snippet above, assuming the blanks were filled in correctly.

Which two adjacent bins in the histogram represent about 50\% of the houses?
[10, 20) and [20, 30)
[20, 30) and [30, 40)
[30, 40) and [40, 50)
[40, 50) and [50, 60)
[50, 60) and [60, 70)
Not possible to determine.
Answer: [20, 30) and
[30, 40)
[20, 30) and
[30, 40) have the two tallest bars, with heights of 0.020
and 0.030, respectively.[20, 30) contributes 0.020
\times 10 = 0.2 or 20\% of the
houses.[30, 40) contributes 0.030
\times 10 = 0.3 or 30\% of the
houses.
The average score on this problem was 83%.
Suppose we create a new histogram, using the same code as above but
with bins = np.arange(0, 90, 20) instead of
bins = np.arange(0, 90, 10). Approximate the height of the
tallest bar in this new histogram. If this is not possible, write “Not
possible to determine."
Answer: 0.025
[0, 20),[20, 40),[40, 60),[60, 80).
The bin [20, 40) merges the original bins
[20, 30) and [30, 40) and would be the bin
with the highest bar in the new histogram.[20, 40):
[20, 30) contributes 0.020
\times 10 = 0.2 (20%).[30, 40) contributes 0.030
\times 10 = 0.3 (30%).[20, 40) is 0.2 +
0.3 = 0.5 or 50\%.
The average score on this problem was 38%.
Suppose we create a new histogram, using the same code as above but
substituting bins = np.arange(0, 90, 5) for
bins = np.arange(0, 90, 10). Approximate the height of the
tallest bar in this new histogram. If this is not possible, write “Not
possible to determine."
Answer: Not possible to determine.
[20, 30)). When switching to 5-unit bins (e.g.,
[20, 25), [25, 30)), we need to know the
distribution of data within the original 10-unit bins to calculate the
new bar heights.[20, 30)
is evenly distributed between [20, 25) and
[25, 30) or concentrated in one of the sub-bins.
The average score on this problem was 70%.
As in the last problem, we’ll continue working with the
tot DataFrame that came from merging trick
with treat. The "price" column contains the
cost in dollars of a single piece of fun-sized candy,
as a float.
In this problem, we want to use tot to calculate the
average cost per piece of Halloween candy at each
house. For example, suppose one house has 30 Twix, which cost \$0.20 each, and 20 Laffy Taffy, which cost
\$0.10 each. Then this house spent
\$8.00 on 50 pieces of candy, for an
average cost of \$0.16 per piece.
Which of the following correctly sets ac to a DataFrame
indexed by "address" with a column called
"avg_cost" that contains the average cost per piece of
Halloween candy at each address? Select all that apply.
Way 1:
ac = tot.groupby("address").sum()
ac = ac.assign(avg_cost = ac.get("price") /
ac.get("how_many")).get(["avg_cost"])Way 2:
ac = tot.assign(x = tot.get("price") / tot.get("how_many"))
ac = ac.groupby("address").sum()
ac = ac.assign(avg_cost = ac.get("x").mean()).get(["avg_cost"])Way 3:
ac = tot.assign(x = tot.get("price") / tot.get("how_many"))
ac = ac.groupby("address").sum()
ac = ac.assign(avg_cost = ac.get("x") /
ac.get("how_many")).get(["avg_cost"])Way 4:
ac = tot.assign(x = tot.get("how_many") * tot.get("price"))
ac = ac.groupby("address").sum()
ac = ac.assign(avg_cost = ac.get("x").mean()).get(["avg_cost"])Way 5:
ac = tot.assign(x = tot.get("how_many") * tot.get("price"))
ac = ac.groupby("address").sum()
ac = ac.assign(avg_cost = ac.get("x") /
ac.get("how_many")).get(["avg_cost"])Way 1
Way 2
Way 3
Way 4
Way 5
Answer: Option 5
We need the average cost per piece at each house.
The correct formula would be: (total spent on candy) / (total pieces of candy)
Let’s go through each Way and assess if it is valid or not.
Way 1: When we sum the “price” column directly, we’re summing the per-piece prices, not the total spent. This gives wrong totals. For example, if a house has 30 pieces at $0.20 and 20 at $0.10, summing prices gives $0.30 instead of $8.00.
Way 2: This first calculates price/quantity for each candy type, then takes the mean of these ratios. This is mathematically incorrect for finding average cost per piece.
Way 3: Similar to Way 2, but even more problematic as it divides by quantity twice.
Way 4: Correctly calculates total spent (x = quantity * price) but then takes the mean of the totals instead of dividing by total quantity.
Way 5: This is correct because:
Using our example:
The average score on this problem was 71%.
What would be the best type of plot to visualize the distribution of
"neighborhood" among the houses represented in
treat?
scatter plot
line plot
bar chart
histogram
Answer: bar chart
The average score on this problem was 76%.
Suppose we had access to historical data about the price of fun-sized candies over time. If we wanted to compare the prices of Milky Way and Skittles over time, which would be the best type of visualization to plot?
overlaid scatter plot
overlaid line plot
overlaid bar chart
overlaid histogram
Answer: overlaid line plot
The average score on this problem was 90%.
Extra Credit
Define the variable double as follows.
double = treat.groupby("candy").count().groupby("address").count()
Now, suppose you know that
double.loc[1].get("how_many") evaluates to
5.
Which of the following is a valid interpretation of this information? Select all that apply.
There are five houses that are each giving out only one type of candy.
There are five types of candy that are each being given out by only one house.
There is only one house that is giving out five types of candy.
There is only one type of candy that is being given out by five houses.
None of these.
Answer: Option 2
Let’s approach this solution by breaking down the line of code into two intermediate steps, so that we can parse them one at a time:
intermediate_one = treat.groupby("candy").count()double = intermediate_one.groupby("address").count()Step 1:
intermediate_one = treat.groupby("candy").count()
The first of our two operations groups the treat
DataFrame by the "candy" column, and aggregates using the
.count() method. This creates an output DataFrame that is
indexed by "candy", where the values in each column
represent the number of times each candy appeared in the
treat DataFrame.
Remember, in our original DataFrame, each row represents one type of
candy being given out by one house. So, each row in
intermediate_one will contain the number of houses
giving out each candy. For example, if the values in the
columns in the row with row label Milky Way were all 3, it would mean that there are 3 houses giving out Milky Ways.
Step 2:
double = intermediate_one.groupby("address").count()
The second of our two operations groups the
intermediate_one DataFrame by the "address"
column, and aggregates using the .count() method. This
creates an output DataFrame that is indexed by "address",
where the values in each column represent the number of times that each
value in the address column appeared in the
intermediate_one DataFrame. However, these are more
difficult to interpret, so let’s break down what this means in the
context of our problem.
The values in the intermediate_one DataFrame represent
how many houses are giving out a specific type of candy (this is the
result of our first operation). So, when we group by these values, the
resulting groups will be defined by all candies that are given out by
the same number of houses. For example, if the values in the columns
with row label 5 were all 2, it would mean that there are 2 types of candy that are being given out by
5 houses. More concretely, this would
mean that the value 5 showed up 2 times in the intermediate_one
DataFrame, which means there must have been 2 candies that were being given out by 5 houses (see above).
Combining these two results, we can interpret the output of our original line of code:
double = treat.groupby("candy").count().groupby("address").count()
outputs a DataFrame where the value in each row represents the number of
different candies that are being given out by the same number of
houses.
Now, we can easily interpret this line of code:
double.loc[1].get("how_many") evaluates to
5.
This means that there are 5 different types of candies that are being given out by only 1 house. This corresponds to Option 2 and only Option 2 in our answer choices, so Option 2 is the correct answer.
The average score on this problem was 15%.