← return to practice.dsc10.com
Instructor(s): Janine Tiefenbruck, Peter Chi
This exam was administered in-person. The exam was closed-notes, except students were allowed to bring their own double-sided cheat sheet. No calculators were allowed. Students had 50 minutes to take this exam.
The English language is considered a challenging language to learn, largely because there are exceptions to just about every “rule”!
In this exam, we’ll work with a data set of English words that appeared in texts used by Indian undergraduate students learning English. The students were asked to read the texts and mark the words they found difficult.
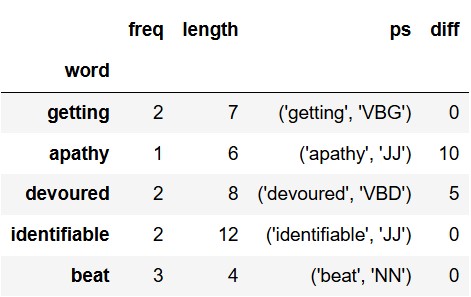
The DataFrame words is indexed by "word"
and contains the following columns:
"freq" (int): The frequency of the word,
or the number of times it appeared in the texts."length" (int): The length of the word, or
the number of letters it contains."ps" (str): The part of speech of the word
(e.g. noun, verb, adjective). This is formatted as an ordered pair,
where the first component is the word, and the second component is a tag
indicating the part of speech (e.g. VBD for past tense verb). The tags
and their meanings are determined by a system known as the Penn Treebank
part of speech tagging system."diff" (int): The number of students who
marked the word difficult.The first few rows of words are shown below, though
there are many more rows than pictured.

Assume that we have already run import babypandas as bpd
and import numpy as np.
Each value in the "ps" column is a string formatted like
"(word, tag)", where the first part is the word and the
second part is a tag indicating the word’s part of speech
(e.g. "(getting, VBG)"). Note that the word and the part of
speech tag are each enclosed in single quotes. To clean the column so
that "ps" contains only the part of speech
tag, we run the following line of code.
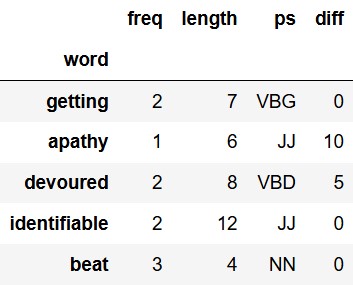
words = words.assign(ps = words.get("ps").apply(fix_ps))After we run this line of code, the first five rows of
words should appear as follows.
Which of the following options correctly define the function
fix_ps to produce the desired result? Select all
that apply.
def fix_ps(x): return x.split("'")[3]
def fix_ps(x): return x.split(",")[1].strip("')")
def fix_ps(x): return x.split(", ")[1].strip("')")
def fix_ps(x): return x.split(", ")[1].strip(")").strip("'")
def fix_ps(x): return x.split(", ")[1].strip("'").strip(")")
None of the above.
Let’s consider all the answer options using
x = "(’getting’, ’VBG’)" as our example.
Option 1:
x.split("’") = ["(", "getting", ", ", "VBG", ")"][3] = "VBG"
This is exactly what we want.
Option 2:
1. x.split(",") = ["(’getting’", " ’VBG’)"][1] = " ’VBG’)"
2. " ’VBG’)" .strip("’)") = " ’VBG"
Note that strip does not remove the exact substring it’s
given; instead, it removes all leading and trailing characters that
appear in the given set of characters.So, this code removes any
leading/trailing instances of single quote "’" and right
parenthesis ")". " ’VBG’)" starts with a
space, which is not in the argument to strip, so nothing is
removed from the front. It ends with both "’" and
")", so both are removed, leaving " ’VBG".
Thus, this option is incorrect.
Option 3:
1. x.split(", ") = ["(’getting’", "’VBG’)"][1] = "’VBG’)"
2. "’VBG’)" .strip("’)") = "VBG"
Here, strip removes any leading and trailing instances of
"’" and ")". "’VBG’)" starts with
"’", which is removed; it ends with "’" and
")", which are also removed, leaving "VBG".
Thus, this option is correct.
Option 4:
1. x.split(", ") = ["(’getting’", "’VBG’)"][1] = "’VBG’)"
2. "’VBG’)" .strip(")") = "’VBG’"
3. "’VBG’" .strip("’") = "VBG"
The first strip removes any leading and trailing instances of
")", so the last character of "’VBG’)" is
removed to become "’VBG’". The second strip removes any
leading and trailing instances of "’", so the first and
last characters of "’VBG’" are removed to become
"VBG". Thus, this option is correct.
Option 5:
1. x.split(", ") = ["(’getting’", "’VBG’)"][1] = "’VBG’)"
2. "’VBG’)".strip(" ’") = "VBG’)"
3. "VBG’)".strip(")") = "VBG’"
The first strip removes any leading and trailing instances of
" " and "’", so the first character of
"’VBG’)" is removed to become "VBG’)". The
second strip removes any leading and trailing instances of
")", so the last character of "VBG’)" is
removed to become "VBG’". Incorrect.
Therefore, the correct options are 1, 3, and 4.
The average score on this problem was 57%.
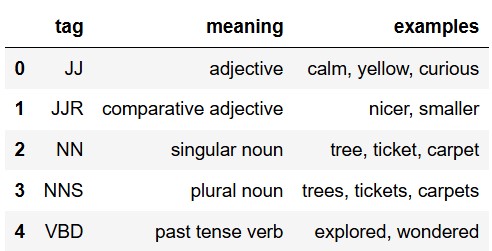
In the early 1990s, computational linguists developed the Penn
Treebank part of speech tagging system. In this system, there are 36 tags that represent different parts of
speech. The tags, their meanings, and a few examples are given in the
tags DataFrame, whose first five rows are shown here.
All of the values in the "ps" column of
words are tags from the Penn Treebank system. Remember,
we’re assuming that we’ve already applied the fix_ps
function from the previous problem.
We want to merge words with tags so that we
can see the meaning of each word’s part of speech tag more easily. Fill
in the blank in the code below to accomplish this.
Note that the index is lost when merging, so in order to keep
"word" as the index of our result, we have to use
reset_index() before merging, then set the index to
"word" again after merging.
merged = words.reset_index().merge(__(a)__).set_index("word")
merged(a): tags, left on="ps", right on="tag"
We want to merge the words dataframe with the tags dataframe, and we
want both to merge on the column with the tags in them. In the words df,
this is the "ps" column, and in the tags df this is the
"tag" column.
The average score on this problem was 75%.
Suppose words contains 5357 rows and tags contains
36 rows. How many rows does
merged contain? Give your answer as an integer or a
mathematical expression that evaluates to an integer.
Answer: 5357
When we merge words with tags, we know that
there are 36 unique rows in tags. This means that for every row in
words, there is only one row in tags that it
will be able to merge with in this new df. This means that every row in
words corresponds to only one row in , meaning that the new
merged df will have the same amount of rows as the words
df, or 5337.
The average score on this problem was 62%.
Below is a bar chart and the code that produced it.
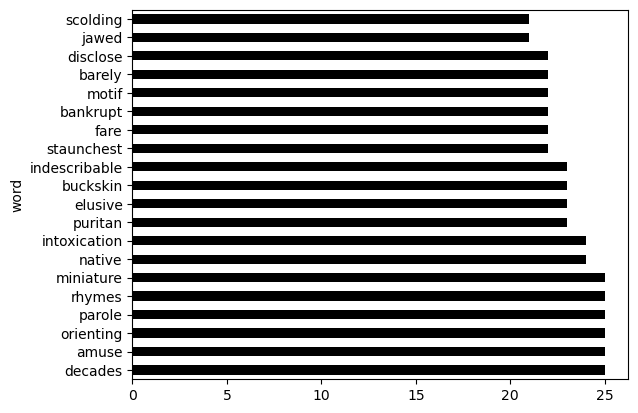
(words.sort_values(by="diff", ascending=False).take(np.arange(20))
.plot(kind='barh', y="diff"));Determine whether each statement below is true or false.
Students found the word “decades" more difficult than any other word.
True
False
Answer: False
We can see on the bar chart that there were 5 other words with the same diff value as decades, so the answer is False.
The average score on this problem was 83%.
If we removed ascending = False from the code, the bar
chart would show the same information, except the bars would appear in
the opposite order from top to bottom.
True
False
Answer: False
We are only plotting the first 20 rows of words after sorting it. So, currently we have plotted the 20 words with the highest diff value. If we removed ascending = False then it would sort in ascending order and we would only be plotting the 20 words with the lowest diff value. They would not be the same words.
The average score on this problem was 46%.
This bar chart shows all words that more than 20 students found
difficult. If we changed np.arange(20) to
np.arange(15) in the code, the bar chart would instead show
all words that more than 15 students found difficult.
True
False
Answer: False
.take(np.arange(20)) takes the elements at those
positional indices. .take(np.arange(15)) would take less
elements, so there is no way that it would include more students in the
bar chart
The average score on this problem was 80%.
The function below classifies the length of a word as
"short", "medium", or "long". Its
input, x, represents the length of a word and will always
be a positive integer.
def classify_length(x):
if x <= 6:
return "short"
elif x <= 10:
return "medium"
else:
return "long"Fill in the blanks of the function below so that
classify_length_2 gives the same output as
classify_length on all positive integer inputs. Each blank
must be filled in with a single line of code.
def classify_length_2(x):
if __(a)__:
return "medium"
if x >= 7:
__(b)__
__(c)__(a): x > 6 and x <= 10
We know that we need to return medium given this condition, so the
answer is x > 6 and x <= 10. x > 6 comes from the
short condition, x = 10 is in the original classify length.
(b): return "long"
Since the condition has x be larger, we know that we should
return "long".
(c): return "short".
This will be the last, non-covered classification, so it should be
return "short".
The average score on this problem was 79%.
Suppose we have a function classify_difficulty that
takes as input the number of students that marked a word difficult, and
returns a difficulty rating of the word: "easy",
"moderate", or "hard". Define the DataFrame
grouped as follows. Note that this uses the
classify_length function from the previous problem.
grouped = (words.assign( diff_category =
words.get("diff").apply(classify_difficulty),
length_category =
words.get("length").apply(classify_length)
)
.groupby(["diff_category", "length_category"])
.count()
.reset_index()
)Suppose there is at least one word with every
possible pair of values for "diff_category" and
"length_category".
How many rows does grouped have? Give your answer as an
integer.
Answer: 9
The code groups the dataframe by two columns, so the number of rows
will be the number of combinations between the two rows. So the two
columns are ‘diff_category’: ("easy", "moderate", "hard") and
‘length_category’: ("short", "medium", "long"), and 3 columns x 3
columns = 9 columns.
The average score on this problem was 77%.
Fill in the blank to set num to the number of words
whose "diff_category" is "hard" and whose
"length_category" is "short". Recall that
.groupby arranges the rows of its output in alphabetical
order.
num = grouped.get("ps").iloc[__(a)__](a): 5
As stated in the last answer, the options for the two indicies are ’diff category’: (”easy”, ”moderate”, ”hard”) and ’length category’: (”short”, ”medium”, ”long”), with ’diff category’ coming first then ’length category’. We want to find the row that is “hard” and ”short”. If we sort each index alphabetically, we get (”easy”, ”hard”, ”moderate”) and (”medium”, ”long”, ”short”). Then, the dataframe looks like ”easy” difficulty for indices 0-2, ”hard” dif- ficulty for 3-5, and medium for 6-8, with each difficulty’s first row being ”medium”, second being ”long”, and last being ”short”. Since we want the hard, short word, we go hard → indices 3-5, then hard and short → index 5.
The average score on this problem was 52%.
We want to determine the proportion of "short" words
that are "hard". Fill in the blanks in the code below such
that prop evaluates to this proportion.
denom = grouped[__(b)__].get("freq").__(c)__
prop = num / denom(b):
grouped.get("length category") == short
We want the proportion of short words that are hard. Remember,
proportions are usually a part of the data divided by the whole sample
space. We already have the row that is the part of the data, which we
did in part b. Therefore, the denom should be the whole sample space,
which in this case is the total amount of short words. So, when we
query, we want only the short words, which we get by querying with
grouped.get("length category") == short.
(c): .sum()
Once we get the freq column, we’re left with one row
indexed by "short" with three subentries for each
difficulty, so we need to use.sum()
The average score on this problem was 38%.
The DataFrame long was created by taking the 500 rows of words corresponding
to words whose "length" is more than 10. Of the 500 words in long,
The density histogram below was created using the data in the
"diff" column of long. The bins
argument was set as bins=np.arange(5, 30, 5) so the
histogram does not include words that fewer than 5
students marked difficult.
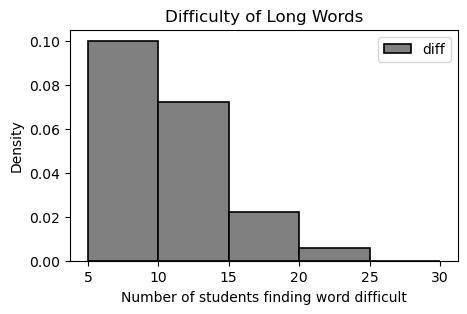
How many words were marked difficult by 10 or more students? Give your answer as an integer.
Answer: 50
To find the number of words marked difficult by 10 or more students,
we can calculate 100 \; - {the number
of words marked difficult by at least 5 students or less than 10
students}, or 100 \; - {the number of
words in bin [5,10)}.
Number of words in bin [5,10) =
(5)(.10)(100) = 50
100 - 50 = 50 words marked difficult
by at least 10 students.
We can also use 1 \; - {proportion of total words in bin [5,10)}, then multiply by 100. Similarly, we can directly calculate the necessary proportion of students by using the area of 3 rightmost bins.
Suppose we regenerated the histogram using the same data, but setting
the bins argument as
bins=np.arange(0, 30, 5).
What would be the height of the bar [5, 10)? Give your answer as a decimal number.
What would be the height of the bar [0, 5)? Give your answer as a decimal number.
Answer (Part 1): 0.02
We know that there are 50 words in the bin [5,10).
Now, however, the histogram is showing all 500 words. So the proportion
of words in bin [5,10) is \frac{50}{500} = 0.1.
To find the height of bar [5,10), we
use:
5 \cdot {h} = 0.1
h = \frac{0.1}{5} = 0.02
Answer (Part 2): 0.16
We know that 100 words were marked difficult by 5 or more students,
so that means 500 - 100 = 400 words
were marked difficult by less than 5 students.
So \frac{400}{500} = 0.8 =
{proportion of total words that less than 5 students found
difficult}.
To find the height of bar [0,5), we use:
5 \cdot {h} = 0.8
h = \frac{0.8}{5} = 0.16
The average score on this problem was 57%.
Fill in the blanks below to estimate the probability that a randomly
generated three-letter lowercase sequence forms a real English word
represented in the words DataFrame.
letters = __(a)__
for letter in "abcdefghijklmnopqrstuvwxyz":
letters = np.append(letters, letter)
repetitions = 10000
found = 0
for i in np.arange(repetitions):
seq = "".join(np.random.choice(__(b)__, 3, replace=True))
if __(c)__:
found = found + 1
prob_real_word = __(d)__
prob_real_word(a): np.array([])
Both arrays and lists are appendable, meaning we can keep adding ele-
ments one by one. We start with an empty container so that in the for
loop, each letter from ”abcdefghijklmnopqrstuvwxyz” can be
added into it. We need this container (letters) so that by the end of
the loop, we have a full collection of all lowercase letters. Later,
we’ll use this collection as the pool to randomly pick letters from. So
whether we start with an empty array (np.array([])) or an
empty list ([]), the purpose is the same to store all 26
lowercase letters that the pro- gram will later draw from when
generating random three-letter words.
(b): letters
The function np.random.choice() randomly selects
elements from a given ar- ray. We want to generate a random 3-letter
sequence from the alphabet.
np.random.choice(letters, 3, replace=True) means “randomly
choose 3 letters from the letters array, allowing repetition.” We use
re- place=True because letters can repeat (e.g., “mom”,
“dad”). The result is something like [’m’, ’o’, ’m’]. Then
””.join(...) combines them into ”mom”.
(c): seq in words.index
After generating a random sequence like ”mom”, we need to check if it’s a real English word. The problem says that the real En- glish words are represented in the index of the DataFrame words. So we use: if seq in words.index: This condition is True when the randomly generated sequence matches a word stored in the dataset. Every time that happens, we increment the counter found by 1.
(d): found / repetitions
Finally, we estimate the probability. The logic is: Probability = (Number of successful outcomes) / (Total trials). In this case, a “successful outcome” is when the randomly generated three-letter sequence that forms an English word appears in the words DataFrame (index). Since we repeated the experiment 10,000 times, prob real world=found/repetitions gives the estimated probability.
The average score on this problem was 65%.
Suppose that for each word in the English language, Matt has a 70\% chance of finding it difficult. Suppose also that the difficulty of each word is independent of the difficulty of any other word.
For all parts of this problem, give your answer as a decimal number or as an unsimplified mathematical expression.
If Matt reads a sentence of 10 words, what is the probability that he finds every word difficult?
Answer: (0.7)^{10}
Each word is independent, so the probability of finding 10 straight words difficult is just the probability of finding any particular word difficult to the tenth power.
The average score on this problem was 89%.
If Matt reads a sentence of 10 words, what is the probability that he finds at least one word difficult?
Answer: 1 - (0.3)^{10}
This is a problem where it’s easier to find the probability that the given event doesn’t happen. The only way this would not happen is if Matt finds absolutely none of the words difficult. That would have a probability of (1-0.7)^{10}, and our answer is going to be 1 minus that.
The average score on this problem was 62%.
Now suppose that Ryan finds the English language slightly more difficult, as it’s not his first language:
For any given word, what is the probability that at least one of Matt and Ryan finds it difficult?
Answer: 1 - 0.3 * 0.5 = 0.85
For this problem its easier to find the probability that this doesn’t happen. The only way this would not happen would be if both Matt and Ryan don’t find the word difficult. For Matt, that happens with probability 0.3. And then given that Matt doesn’t find the word difficult, Ryan has a 0.5 probability of not finding the word difficult. Multiplying those two probabilities and subtracting from 1 gives us our answer.
The average score on this problem was 34%.
What is the probability that for every word in a sentence of 10 words, exactly one of Matt and Ryan finds the word difficult?
Answer: (0.7 * 0.1 + 0.3 * 0.5)^{10} = (0.22)^{10}
Since each word is independent, we only need to find the probability that for one particular word either Matt or Ryan finds it difficult but not both, and then we can take that probability to the power of 10. The first case is that Matt finds a word difficult but Ryan doesn’t. The first part happens with probability 0.7, and given that Matt found the word difficult, the second part happens with probability 0.1. We multiply those to get one part of our sum. The other case is that Matt doesn’t find a word difficult but Ryan does. The first part happens with probability 0.3, and given that, the second part happens with probability 0.5. Multiplying these two gives us the second part of our sum.
The average score on this problem was 17%.