← return to practice.dsc10.com

This quiz was administered in-person. Students were allowed 1 double-sided cheatsheet. Students had 20 minutes to work on the quiz.

This quiz covered Lectures 16-18 of the Fall 2025 offering of DSC 10.

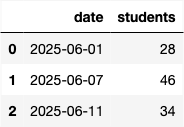
Ryan works at Geisel Library. He counts the number of students on Geisel’s second floor at 10 AM for some days in summer and fall, storing them in DataFrames summer (top) and fall (bottom). The first few rows are shown, along with the mean and standard deviation of the "students" column.

summer

Mean = 40
SD = 10

fall

Mean = 400
SD = 10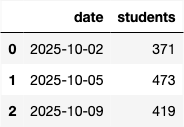

Problem 1

At least what proportion of summer.get("students") is in the range [30,40]?

• \geq 0.75

• \geq 0.68

• \geq 0.25

• \geq 0.00

Problem 2

Ryan runs the code below to make a single array with the contents of the "students" columns from both summer and fall.

    combined = np.append(summer.get("students"), fall.get("students"))

Problem 2.1

Select all of the true statements below:

• The mean of combined is 220.

• The mean of combined is in the range (40,400).

• The standard deviation of combined is less than 10.

• The standard deviation of combined is greater than 10.

• None of the above.

Problem 2.2

Since he was in a rush, Ryan asked ChatGPT to write code that standardizes combined. To his surprise, 90\% of the standardized data is less than 0. Which of the following best explains this situation?

• Ryan should be surprised; this must have incorrectly standardized the data.

• Ryan should be surprised; a number of students cannot be negative.

• Ryan should not be surprised; it’s possible for 100\% of the data to be below 0.

• Ryan should not be surprised; his data is skewed.

Problem 3

For this question only, suppose we know that summer.get("students") is normally distributed. You randomly select one number from summer.get("students"). Using the function scipy.stats.norm.cdf, write one line of code that evaluates to the probability that the number you selected is in the range [30,45].

Problem 4

Ryan writes the following code to obtain a 95% bootstrapped confidence interval for the mean number of students in Geisel’s second floor at 10AM in the fall only:

stats = np.array([])
for i in range(3333):
    stat = fall.sample(fall.shape[0], 
                       replace=True).get("students").mean()
    stats = np.append(stats, stat)
lower = np.percentile(stats, 2.5)
upper = np.percentile(stats, 97.5)

Problem 4.1

Write one line of code that evaluates to the upper endpoint of the 95\% CLT-based confidence interval for this same parameter. Recall that some potentially relevant values are provided with the DataFrames on the previous page.

Problem 4.2

True or False: The 95\% confidence interval generated by the bootstrapping code above cannot be narrower than a 95% confidence interval generated by the Central Limit Theorem.

• True

• False

Problem 4.3

True or False: The Central Limit Theorem tells us that the data in fall.get("students") is roughly normally distributed.

• True

• False

Problem 4.4

True or False: To obtain a 95% bootstrapped confidence interval for the median, we can simply change .mean() to .median() in the original code above.

• True

• False

Problem 4.5

True or False: We can use the CLT to create a valid 95\% confidence interval for the median.

• True

• False

Problem 5

Suppose Ryan is interested in collecting data and using it to form a 95\% confidence interval for the proportion of UCSD students that have ever been to Geisel library.

Write an expression that evaluates to the minimum sample size required for the confidence interval to have a width of at most 0.2.

👋 Feedback: Find an error? Still confused? Have a suggestion? Let us know here.