← return to practice.dsc10.com
Below are practice problems tagged for Lecture 11 (rendered directly from the original exam/quiz sources).
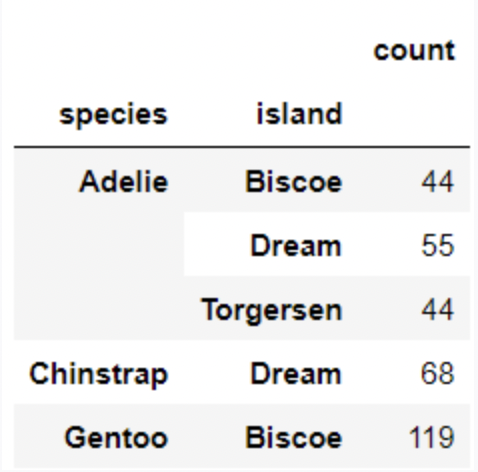
Each individual penguin in our dataset is of a certain species (Adelie, Chinstrap, or Gentoo) and comes from a particular island in Antarctica (Biscoe, Dream, or Torgerson). There are 330 penguins in our dataset, grouped by species and island as shown below.

Suppose we pick one of these 330 penguins, uniformly at random, and name it Chester.
What is the probability that Chester comes from Dream island? Give your answer as a number between 0 and 1, rounded to three decimal places.
Answer: 0.373
P(Chester comes from Dream island) = # of penguins in dream island / # of all penguins in the data = \frac{55+68}{330} \approx 0.373
The average score on this problem was 94%.
If we know that Chester comes from Dream island, what is the probability that Chester is an Adelie penguin? Give your answer as a number between 0 and 1, rounded to three decimal places.
Answer: 0.447
P(Chester is an Adelie penguin given that Chester comes from Dream island) = # of Adelie penguins from Dream island / # of penguins from Dream island = \frac{55}{55+68} \approx 0.447
The average score on this problem was 91%.
If we know that Chester is not from Dream island, what is the probability that Chester is not an Adelie penguin? Give your answer as a number between 0 and 1, rounded to three decimal places.
Answer: 0.575
Method 1
P(Chester is not an Adelie penguin given that Chester is not from Dream island) = # of penguins that are not Adelie penguins from islands other than Dream island / # of penguins in island other than Dream island = \frac{119\ \text{(eliminate all penguins that are Adelie or from Dream island, only Gentoo penguins from Biscoe are left)}}{44+44+119} \approx 0.575
Method 2
P(Chester is not an Adelie penguin given that Chester is not from Dream island) = 1- (# of penguins that are Adelie penguins from islands other than Dream island / # of penguins in island other than Dream island) = 1-\frac{44+44}{44+44+119} \approx 0.575
The average score on this problem was 85%.
Suppose you are booking a flight and you have no control over which airline you fly on. Below is a table with multiple airlines and the probability of a flight being on a specific airline.
| Airline | Chance |
|---|---|
| Delta | 0.4 |
| United | 0.3 |
| American | 0.2 |
| All other airlines | 0.1 |
The airline for one flight has no impact on the airline for another flight.
For this question, suppose that you schedule 3 flights for January 2022.
What is the probability that all 3 flights are on United? Give your answer as an exact decimal between 0 and 1 (not a Python expression).
Answer: 0.027
For all three flights to be on United, we need the first flight to be on United, and the second, and the third. Since these are independent events that do not impact one another, and we need all three flights to separately be on United, we need to multiply these probabilities, giving an answer of 0.3*0.3*0.3 = 0.027.
Note that on an exam without calculator access, you could leave your answer as (0.3)^3.
The average score on this problem was 93%.
What is the probability that all 3 flights are on Delta, or all on United, or all on American? Give your answer as an exact decimal between 0 and 1 (not a Python expression).
Answer: 0.099
We already calculated the probability of all three flights being on United as (0.3)^3 = 0.027. Similarly, the probability of all three flights being on Delta is (0.4)^3 = 0.064, and the probability of all three flights being on American is (0.2)^3 = 0.008. Since we cannot satisfy more than one of these conditions at the same time, we can separately add their probabilities to find a total probability of 0.027 + 0.064 + 0.008 = 0.099.
The average score on this problem was 76%.
True or False: The probability that all 3 flights are on the same airline is equal to the probability you computed in the previous subpart.
True
False
Answer: False
It’s not quite the same because the previous subpart doesn’t include the probability that all three flights are on the same airline which is not one of Delta, United, or American. For example, there is a small probability that all three flights are on Allegiant or all three flights are on Southwest.
The average score on this problem was 90%.
It turns out that King Triton is so busy that he doesn’t even book his own flights – he has a travel agent who books his flights for him. He doesn’t get to choose the airline that he flies on, but his travel agent gave him the following table, which describes the probability of each of his flights in 2022 being on Delta, United, American, or another airline:
| Airline | Chance |
|---|---|
| Delta | 0.4 |
| United | 0.3 |
| American | 0.2 |
| All other airlines | 0.1 |
The airline for one flight has no impact on the airline for another flight.
For this question, suppose that King Triton schedules 3 flights for January 2022.
What is the probability that all 3 flights are on United? Give your answer as an exact decimal between 0 and 1 (not a Python expression).
Answer: 0.027
For all three flights to be on United, we need the first flight to be on United, and the second, and the third. Since these are independent events that do not impact one another, and we need all three flights to separately be on United, we need to multiply these probabilities, giving an answer of 0.3*0.3*0.3 = 0.027.
Note that on an exam without calculator access, you could leave your answer as (0.3)^3.
The average score on this problem was 93%.
What is the probability that all 3 flights are on Delta, or all on United, or all on American? Give your answer as an exact decimal between 0 and 1 (not a Python expression).
Answer: 0.099
We already calculated the probability of all three flights being on United as (0.3)^3 = 0.027. Similarly, the probability of all three flights being on Delta is (0.4)^3 = 0.064, and the probability of all three flights being on American is (0.2)^3 = 0.008. Since we cannot satisfy more than one of these conditions at the same time, we can separately add their probabilities to find a total probability of 0.027 + 0.064 + 0.008 = 0.099.
The average score on this problem was 76%.
True or False: The probability that all 3 flights are on the same airline is equal to the probability you computed in the previous subpart.
True
False
Answer: False
It’s not quite the same because the previous subpart doesn’t include the probability that all three flights are on the same airline which is not one of Delta, United, or American. For example, there is a small probability that all three flights are on Allegiant or all three flights are on Southwest.
The average score on this problem was 90%.
Below, we define a new DataFrame called
seven_apps and display it fully.
seven_apps = apps.sample(7).sort_values(by="dependents", ascending=False)
seven_apps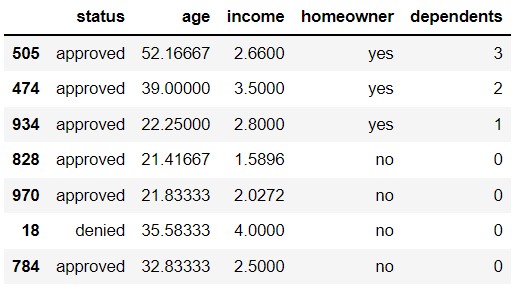
Consider the process of resampling 7 rows from
seven_apps with replacement, and computing the
maximum number of dependents in the resample.
If we take one resample, what is the probability that the maximum number of dependents in the resample is less than 3? Leave your answer unsimplified.
Answer: \left( 1 - \frac{1}{7}\right)^7 = \left( \frac{6}{7}\right)^7
Of the 7 rows in the seven_apps DataFrame, there are 6
rows that have a value less than 3 in the dependents
column. This means that if we were to sample one row
from seven_apps, there would be a \frac{6}{7} chance of selecting one of the
rows that has less than 3 dependents. The question is asking what the
probability that the maximum number of dependents in the resample is
less than 3. One resample of the DataFrame is equivalent to sampling one
row from seven_apps 7 different times, without replacement.
So the probability of getting a row with less than 3 dependents, 7 times
consecutively, is \left(
\frac{6}{7}\right)^7.
The average score on this problem was 47%.
If we take 50 resamples, what is the probability that the maximum number of dependents is never 3, in any resample? Leave your answer unsimplified.
Answer: \left[ \left( 1 - \frac{1}{7}\right)^7 \right]^{50} = \left( \frac{6}{7}\right)^{350}
We know from the previous part of this question that the probability
of one resample of seven_apps having a maximum number of
dependents less than 3 is \left(
\frac{6}{7}\right)^7. Now we must repeat this process 50 times
independently, and so the probability that all 50 resamples have a
maximum number of dependents less than 3 is \left(\left( \frac{6}{7}\right)^{7}\right)^{50} =
\left( \frac{6}{7}\right)^{350}. Another way to interpret this is
that we must select 350 rows, one a time, such that none of them are the
one row containing 3 dependents.
The average score on this problem was 41%.
If we take 50 resamples, what is the probability that the maximum number of dependents is 3 in every resample? Leave your answer unsimplified.
Answer: \left[1 - \left( 1 - \frac{1}{7}\right)^7 \right]^{50} = \left[1 - \left( \frac{6}{7}\right)^7 \right]^{50}
We’ll first take a look at the probability of one
resample of seven_apps having the maximum number
of dependents be 3. In order for this to happen, at least one row of the
7 selected for the resample must be the row containing 3 dependents. The
probability of getting this row at least once is equal to the complement
of the probability of never getting this row, which we calculated in
part (a) to be \left(
\frac{6}{7}\right)^7. Therefore, the probability that at least
one row in the resample has 3 dependents, is 1
-\left( \frac{6}{7}\right)^7.
Now that we know the probability of getting one resample where the maximum number of dependents is 3, we can calculate the probability that the same thing happens in 50 independent resamples by multiplying this probability by itself 50 times. Therefore, the probability that the maximum number of dependents is 3 in each of 50 resamples is \left[1 - \left( \frac{6}{7}\right)^7 \right]^{50}.
The average score on this problem was 27%.
At TritonCard, a new UCSD alumni-run credit card company, applications are approved at random. Each time someone submits an application, a TritonCard employee rolls a fair six-sided die two times. If both rolls are the same even number — that is, if both are 2, both are 4, or both are 6 — TritonCard approves the application. Otherwise, they reject it.
You submit k identical TritonCard applications. The probability that at least one of your applications is approved is of the form 1-\left(\frac{a}{b}\right)^k. What are the values of a and b? Give your answers as integers such that the fraction \frac{a}{b} is fully simplified.
Answer: a = 11, b = 12
The format of the answer suggests we should use the complement rule. The opposite of at least one application being approved is that no applications are approved, or equivalently, all applications are denied.
Consider one application. Its probability of being approved is \frac{3}{6}*\frac{1}{6} = \frac{3}{36} = \frac{1}{12} because we need to get any one of the three even numbers on the first roll, then the second roll must match the first. So one application has a probability of being denied equal to \frac{11}{12}.
Therefore, the probability that all k applications are denied is \left(\frac{11}{12}\right)^k. The probability that this does not happen, or at least one is approved, is given by 1-\left(\frac{11}{12}\right)^k.
The average score on this problem was 41%.
Every TritonCard credit card has a 3-digit security code on the back, where each digit is a number 0 through 9. There are 1,000 possible 3-digit security codes: 000, 001, \dots, 998, 999.
Tony, the CEO of TritonCard, wants to only issue credit cards whose security codes satisfy all of the following criteria:
The first digit is odd.
The middle digit is 0.
The last digit is even.
Tony doesn’t have a great way to generate security codes meeting these three criteria, but he does know how to generate security codes with three unique (distinct) digits. That is, no number appears in the security code more than once. So, Tony decides to randomly select a security code from among those with three unique digits. If the randomly selected security code happens to meet the desired criteria, TritonCard will issue a credit card with this security code, otherwise Tony will try his process again.
What is the probability that Tony’s first randomly selected security code satisfies the given criteria? Give your answer as a fully simplified fraction.
Answer: \frac{1}{36}
Imagine generating a security code with three unique digits by selecting one digit at a time. In other words, we would need to select three values without replacement from the set of digits 0, 1, 2, \dots, 9. The probability that the first digit is odd is \frac{5}{10}. Then, assuming the first digit is odd, the probability of the middle digit being 0 is \frac{1}{9} since only nine digits are remaining, and one of them must be 0. Then, assuming we have chosen an odd number for the first digit and 0 or the middle digit, there are 8 remaining digits we could select, and only 4 of them are even, so the probability of the third digit being even is \frac{4}{8}. Multiplying these all together gives the probability that all three criteria are satisfied: \frac{5}{10} \cdot \frac{1}{9} \cdot \frac{4}{8} = \frac{1}{36}
The average score on this problem was 38%.
Daphne, the newest employee at TritonCard, wants to try a different way of generating security codes. She decides to randomly select a 3-digit code from among all 1,000 possible security codes (i.e. the digits are not necessarily unique). As before, if the code randomly selected code happens to meet the desired criteria, TritonCard will issue a credit card with this security code, otherwise Daphne will try her process again.
What is the probability that Daphne’s first randomly selected security code satisfies the given criteria? Give your answer as a fully simplified fraction.
Answer: \frac{1}{40}
We’ll use a similar strategy as in the previous part. This time, however, we need to select three values with replacement from the set of digits 0, 1, 2, \dots, 9. The probability that the first digit is odd is \frac{5}{10}. Then, assuming the first digit is odd, the probability of the middle digit being 0 is \frac{1}{10} since any of the ten digits can be chosen, and one of them is 0. Then, assuming we have chosen an odd number for the first digit and 0 or the middle digit, the probability of getting an even number for the third digit is \frac{5}{10}, which actually does not depend at all on what we selected for the other digits. In fact, when we sample with replacement, the probabilities of each digit satisfying the given criteria don’t depend on whether the other digits satisfied the given criteria (in other words, they are independent). This is different from the previous part, where knowledge of previous digits satisfying the criteria informed the chances of the next digit satisfying the criteria. So for this problem, we can really just think of each of the three digits separately and multiply their probabilties of meeting the desired criteria: \frac{5}{10} \cdot \frac{1}{10} \cdot \frac{5}{10} = \frac{1}{40}
The average score on this problem was 51%.
The DataFrame below shows the distribution of
"BodyStyle" for all "Brands" in
evs, other than Nissan. We will call EVs made by a
"Brand" other than Nissan “non-Nissan EVs”; there are 24
non-Nissan EVs in evs.
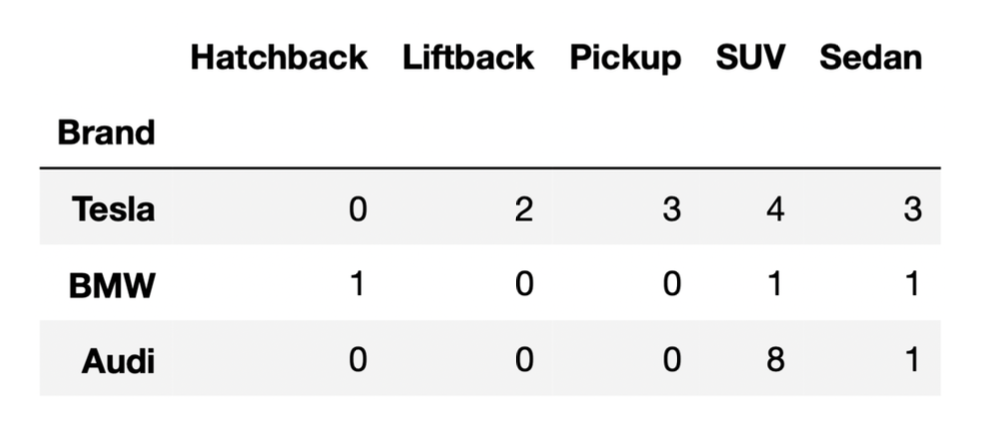
Use the information above to answer the following questions.
Suppose we randomly select one of the non-Nissan EVs and it is either
an SUV or a sedan. What is the most likely "Brand" of the
randomly selected non-Nissan EV?
Tesla
BMW
Audi
Answer: Audi
Let’s compute the number of EVs that are either SUVs or sedans for each non-Nissan Brand. (To do this, we’ll look at the right-most two columns in the DataFrame provided.)
Since Audi is the "Brand" with the most total SUVs and
sedans, it is the most likely "Brand" to be selected.
Note: You could compute conditional probabilities for each
brand, if you’d like, by dividing the counts above by 18 (the total
number of SUVs and sedans). For instance, P(\text{EV is a BMW given that EV is an SUV or
sedan}) = \frac{2}{18}. The "Brand" with the highest
count (Audi, with 9 SUVs or sedans) is also the "Brand"
with the highest conditional probability of being selected given that
the selected car is an SUV or sedan (Audi, with \frac{9}{18}).
The average score on this problem was 88%.
Suppose we randomly select two of the non-Nissan EVs without replacement. The probability that both are BMWs is equal to \frac{1}{k} , where k is a positive integer. What is k?
8
56
64
84
92
108
Answer: 92
In the first selection, the probability of selecting a BMW is \frac{1+1+1}{24} = \frac{3}{24} (3 is the total number of EVs that are BMW, and 24 is the total number of non-Nissan EVs as given by the question).
In the second selection, since we select without replacement, there are only 23 EVs we can select from. Given that in the first selection we already selected 1 BMW, there are only 2 BMWs left among the 23 EVs left. Thus, the probability of getting a BMW in the second selection is \frac{2}{23}.
Putting this all together, the probability that both selections are BMWs is
\frac{3}{24}\cdot\frac{2}{23} = \frac{6}{24} \cdot \frac{1}{23} =\frac{1}{4} \cdot \frac{1}{23} = \frac{1}{92}
So, k = 92.
The average score on this problem was 67%.
Suppose we randomly select one of the non-Nissan EVs and it is an SUV. What is the probability that it is made by Tesla? Give your answer as a simplified fraction.
Answer: \frac{4}{13}
The question is asking for the proportion of SUVs that are made by Tesla.
We first need to find the number of SUVs in the DataFrame provided, which is 4 + 1 + 8 = 13. Of those 13 SUVs, 4 are made by Tesla. Thus, the proportion of SUVs made by Tesla is \frac{4}{13}, so the probability that a randomly selected SUV is made by Tesla is \frac{4}{13}.
The average score on this problem was 66%.
The DataFrame ten_txns, displayed in its
entirety below, contains a simple random sample of 10 rows from
txn.
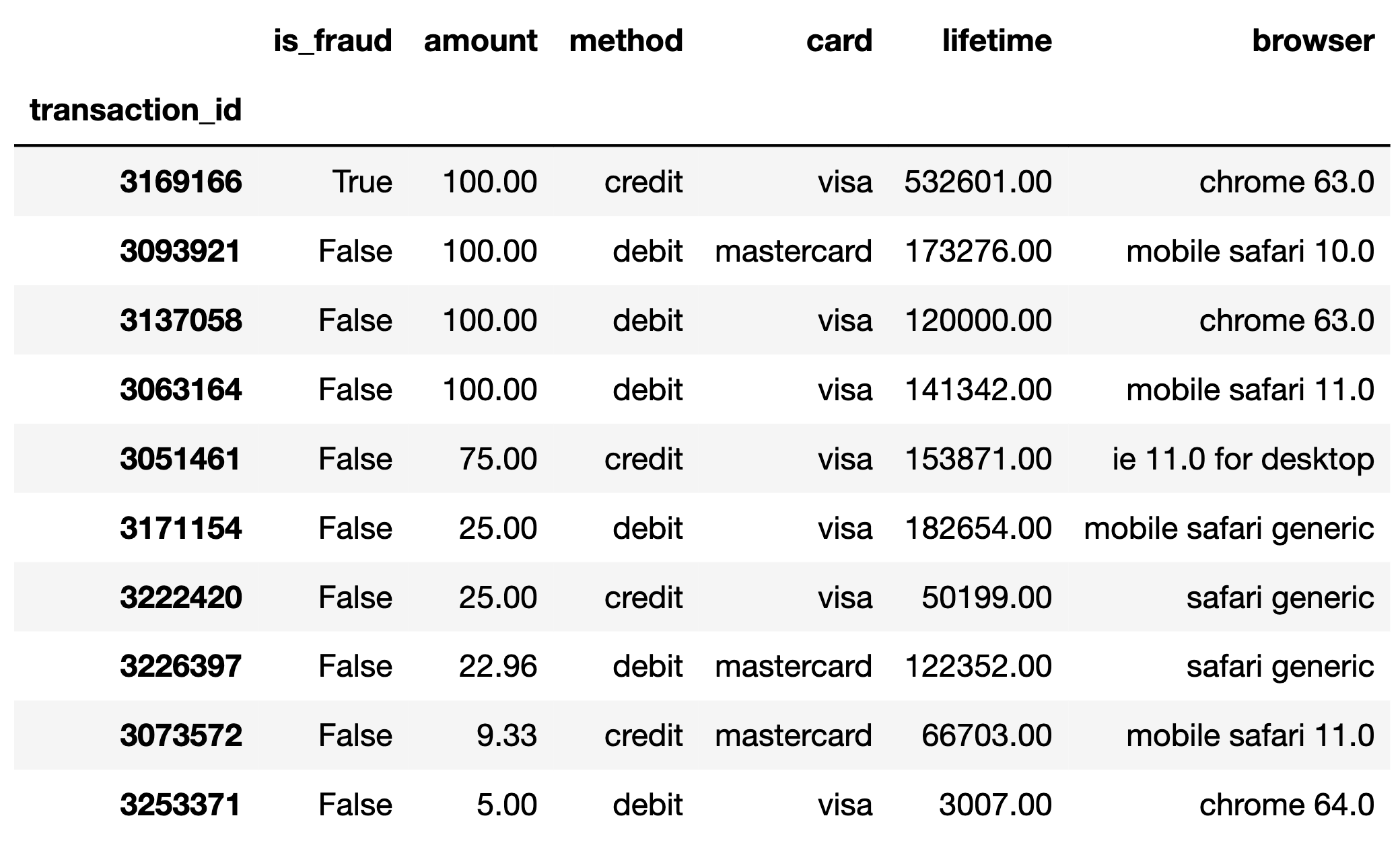
Suppose we randomly select one transaction from
ten_txns. What is the probability that the selected
transaction is made with a "card" of
"mastercard" or a "method" of
"debit"? Give your answer either as an exact decimal or a
simplified fraction.
Answer: 0.7
We can simply count the number of transactions meeting at least one
of the two criteria. More easily, there are only 3 rows that do not meet
either of the criteria (the rows that are "visa" and
"credit" transactions). Therefore, the probability is 7 out
of 10, or 0.7. Note that we cannot simply add up the probability of
"mastercard" (0.3) and the probability of
"debit" (0.6) since there is overlap between these. That
is, some transactions are both "mastercard" and
"debit".
The average score on this problem was 64%.
Suppose we randomly select two transactions from
"ten_txns", without replacement, and learn that neither of
the selected transactions is for an amount of 100 dollars. Given this
information, what is the probability that:
the first transaction is made with a "card" of
"visa" and a "method" of "debit",
and
the second transaction is made with a "card" of
"visa" and a "method" of
"credit"?
Give your answer either as an exact decimal or a simplified fraction.
Answer: \frac{2}{15}
We know that the sample space here doesn’t have any of the $100
transactions, so we can ignore the first 4 rows when calculating the
probability. In the remaining 6 rows, there are exactly 2 debit
transactions with "visa" cards, so the probability of our
first transaction being of the specified type is \frac{2}{6}. There are also two credit
transactions with "visa" cards, but the denominator of the
probability of the second transaction is 5 (not 6), since the sample
space was reduced by one after the first transaction. We’re choosing
without replacement, so you can’t have the same transaction in your
sample twice. Thus, the probability of the second transaction being a
visa credit card is \frac{2}{5}. Now,
we can apply the multiplication rule, and we have that the probability
of both transactions being as described is \frac{2}{6} \cdot \frac{2}{5} = \frac{4}{30} =
\frac{2}{15}.
The average score on this problem was 45%.
For your convenience, we show ten_txns again below.

Suppose we randomly select 15 rows, with replacement, from
ten_txns. What’s the probability that in our selection of
15 rows, the maximum transaction amount is less than 25 dollars?
\frac{3}{10}
\frac{3}{15}
\left(\frac{3}{10}\right)^{3}
\left(\frac{3}{15}\right)^{3}
\left(\frac{3}{10}\right)^{10}
\left(\frac{3}{15}\right)^{10}
\left(\frac{3}{10}\right)^{15}
\left(\frac{3}{15}\right)^{15}
Answer: \left(\frac{3}{10}\right)^{15}
There are only 3 rows in the sample with a transaction amount under $25, so the chance of choosing one transaction with such a low value is \frac{3}{10}. For the maximum transaction amount to be less than 25 dollars, this means all transaction amounts in our sample have to be less than 25 dollars. To find the chance that all transactions are for less than $25, we can apply the multiplication rule and multiply the probability of each of the 15 transactions being less than $25. Since we’re choosing 15 times with replacement, the events are independent (choosing a certain transaction on the first try won’t affect the probability of choosing it again later), so all the terms in our product are \frac{3}{10}. Thus, the probability is \frac{3}{10} * \frac{3}{10} * \ldots * \frac{3}{10} = \left(\frac{3}{10}\right)^{15}.
The average score on this problem was 89%.
King Triton had four children, and each of his four children started their own families. These four families organize a Triton family reunion each year. The compositions of the four families are as follows:
Family W: "1a4c"
Family X: "2a1c"
Family Y: "2a3c"
Family Z: "1a1c"
Suppose we choose one of the fifteen people at the Triton family reunion at random.
Given that the chosen individual is from a family with one child, what is the probability that they are from Family X? Give your answer as a simplified fraction.
Answer: \frac{3}{5}
Given that the chosen individual is from a family with one child, we know that they must be from either Family X or Family Z. There are three individuals in Family X, and there are a total of five individuals from these two families. Thus, the probability of choosing any one of the three individuals from Family X out of the five individuals from both families is \frac{3}{5}.
The average score on this problem was 43%.
Consider the events A and B, defined below.
A: The chosen individual is an adult.
B: The chosen individual is a child.
True or False: Events A and B are independent.
True
False
Answer: False
If two events are independent, knowledge of one event happening does not change the probability of the other event happening. In this case, events A and B are not independent because knowledge of one event gives complete knowledge of the other.
To see this, note that the probability of choosing a child randomly out of the fifteen individuals is \frac{9}{15}. That is, P(B) = \frac{9}{15}.
Suppose now that we know that the chosen individual is an adult. In this case, the probability that the chosen individual is a child is 0, because nobody is both a child and an adult. That is, P(B \text{ given } A) = 0, which is not the same as P(B) = \frac{9}{15}.
This problem illustrates the difference between mutually exclusive events and independent events. In this case A and B are mutually exclusive, because they cannot both happen. But that forces them to be dependent events, because knowing that someone is an adult completely determines the probability that they are a child (it’s zero!)
The average score on this problem was 33%.
Consider the events C and D, defined below.
C: The chosen individual is a child.
D: The chosen individual is from family Y.
True or False: Events C and D are independent.
True
False
Answer: True
If two events are independent, the probability of one event happening does not change when we know that the other event happens. In this case, events C and D are indeed independent.
If we know that the chosen individual is a child, the probability that they come from Family Y is \frac{3}{9}, which simplifies to \frac{1}{3}. That is P(D \text{ given } C) = \frac{1}{3}.
On the other hand, without any prior knowledge, when we select someone randomly from all fifteen individuals, the probability they come from Family Y is \frac{5}{15}, which also simplifies to \frac{1}{3}. This says P(D) = \frac{1}{3}.
In other words, knowledge of C is irrelevant to the probability of D occurring, which means C and D are independent.
The average score on this problem was 35%.
At the reunion, the Tritons play a game that involves placing the four letters into a hat (W, X, Y, and Z, corresponding to the four families). Then, five times, they draw a letter from the hat, write it down on a piece of paper, and place it back into the hat.
Let p = \frac{1}{4} in the questions that follow.
What is the probability that Family W is selected all 5 times?
p^5
1 - p^5
1 - (1 - p)^5
(1 - p)^5
p \cdot (1 - p)^4
p^4 (1 - p)
None of these.
Answer: p^5
The probability of selecting Family W in the first round is p, which is the same for the second round, the third round, and so on. Each of the chosen letters is drawn independently from the others because the result of one draw does not affect the result of the next. We can apply the multiplication rule here and multiply the probabilities of choosing Family W in each round. This comes out to be p\cdot p\cdot p\cdot p\cdot p, which is p^5.
The average score on this problem was 91%.
What is the probability that Family W is selected at least once?
p^5
1 - p^5
1 - (1 - p)^5
(1 - p)^5
p \cdot (1 - p)^4
p^4 (1 - p)
None of these.
Answer: 1 - (1 - p)^5
Since there are too many ways that Family W can be selected to meet the condition that it is selected at least once, it is easier if we calculate the probability that Family W is never selected and subtract that from 1. The probability that Family W is not selected in the first round is 1-p, which is the same for the second round, the third round, and so on. We want this to happen for all five rounds, and since the events are independent, we can multiply their probabilities all together. This comes out to be (1-p)^5, which represents the probability that Family W is never selected. Finally, we subtract (1-p)^5 from 1 to find the probability that Family W is selected at least once, giving the answer 1 - (1-p)^5.
The average score on this problem was 62%.
What is the probability that Family W is selected exactly once, as the last family that is selected?
p^5
1 - p^5
1 - (1 - p)^5
(1 - p)^5
p \cdot (1 - p)^4
p^4 (1 - p)
None of these.
Answer: p \cdot (1 - p)^4
We want to find the probability of Family W being selected only as the last draw, and not in the first four draws. The probability that Family W is not selected in the first draw is (1-p), which is the same for the second, third, and fourth draws. For the fifth draw, the probability of choosing Family W is p. Since the draws are independent, we can multiply these probabilities together, which comes out to be (1-p)^4 \cdot p = p\cdot (1-p)^4.
The average score on this problem was 67%.
At the beginning of 2025, avid reader Michelle will join the Blind Date with a Book program sponsored by Bill’s Book Bonanza. Once a month from January through December, Michelle will receive a surprise book in the mail from the bookstore. So she’ll get 12 books throughout the year.
Each book is randomly chosen among those available at the bookstore
(or equivalently, from among those in the bookstore
DataFrame). Each book is equally likely to be chosen each month, and
each month’s book is chosen independently of all others, so repeats can
occur.
Let p be the proportion of books in
bookstore from the romance genre (0 \leq p \leq 1).
What is the probability that the books Michelle receives in February and December are romance, while the books she receives all other months are non-romance? Your answer should be an unsimplified expression in terms of p.
Answer: (1 - p)^{10} * p^2
The probability of February and December being romance is p for each of those two months, and the probability of any one of the other months being non-romance is 1-p. We multiply all twelve of these probabilities since the months are independent, and the result is p^2(1−p)^{10}.
The average score on this problem was 57%.
What is the probability that at least one of the books Michelle receives in the last four months of the year is romance? Your answer should be an unsimplified expression in terms of p.
Answer: 1 - (1 - p)^4
To solve this, we calculate the probability that none of the last four months contains romance, which is (1−p)^4. Taking the complement gives us the probability that at least one of the last four months is romance: 1−(1−p)^4. The two possible situations are: no romance and at least one romance, so together they must add up to one, which is why we can use the complement.
The average score on this problem was 51%.
It is likely Michelle will receive at least one romance book and at least one non-romance book throughout the 12 months of the year. What is the probability that this does not happen? Your answer should be an unsimplified expression in terms of p.
Answer: p^{12} + (1 - p)^{12}
In this case, there are only two scenarios to consider: either all 12 books are non-romance, which gives (1−p)^{12}, or all 12 books are romance, which gives p^{12}. Adding these together gives p^{12}+(1−p)^{12}.
The average score on this problem was 29%.
Let n be the total number of rows in
bookstore. What is the probability that Michelle does not
receive any duplicate books in the first four months of the year? Your
answer should be an unsimplified expression in terms of n.
Answer: \frac{(n - 1)}{n} * \frac{(n - 2)}{n} * \frac{(n - 3)}{n}
For there to be no duplicate books in the first four months, each subsequent book must be different from the previous ones. After selecting the first book (which will always be undiplicated), the second book has \frac{(n - 1)}{n} probability of being unique, the third \frac{(n - 2)}{n}, and the fourth \frac{(n - 3)}{n}. If you like, you can think of the probability of the first book being unique as \frac{n}{n} and include it in your answer.
The average score on this problem was 31%.
Now, consider the following lines of code which define variables
i, j, and k.
def foo(x, y):
if x == "rating":
z = bookstore[bookstore.get(x) > y]
elif x == "genre":
z = bookstore[bookstore.get(x) == y]
return z.shape[0]
i = foo("rating", 3)
j = foo("rating", 4)
k = foo("genre", "Romance")For both questions that follow, your answer should be an unsimplified
expression in terms of i, j, k
only. If you do not have enough information to determine the answer,
leave the answer box blank and instead fill in the bubble that says “Not
enough information”.
If we know in advance that Michelle’s January book will have a rating greater than 3, what is the probability that the book’s rating is greater than 4?
Answer: j/i
Looking at the code, we can see that i represents the
number of books with a rating greater than 3, and j
represents the number of books with a rating greater than 4. This is a
conditional probability question: find the probability that Michelle’s
book has a rating greater than 4 given that it has a rating greater than
3. Since we already know Michelle’s book has a rating higher than 3, the
denominator, representing the possible books she could get, should be
i. The numerator represents the books that meet our desired
condition of having a rating greater than 4, which is j.
Therefore, the result is j/i.
The average score on this problem was 53%.
If we know in advance that Michelle’s January book will have a rating greater than 3, what is the probability that the book’s genre is romance?
Although i represents the total number of books with a
rating greater than 3 and k represents the number of
romance books, there is no information about how many romance books have
a rating greater than 3. Thus we cannot find the answer without
additional information.
The average score on this problem was 71%.
Suppose you visit a house that has 40 Twix, 50 M&Ms, and 10 KitKats in a bowl. You take three pieces of candy from this bowl.
What is the probability you get all Twix?
\dfrac{40}{100} \cdot \dfrac{39}{100} \cdot \dfrac{38}{100}
\dfrac{40}{100} \cdot \dfrac{40}{99} \cdot \dfrac{40}{98}
\dfrac{40}{100} \cdot \dfrac{40}{100} \cdot \dfrac{40}{100}
\dfrac{40}{100} \cdot \dfrac{39}{99} \cdot \dfrac{38}{98}
Answer: \dfrac{40}{100} \cdot \dfrac{39}{99} \cdot \dfrac{38}{98}
We need to find the probability that we get all Twix among the three candies selected from the bowl. Since we are selecting three times from the same bowl, we know that we are selecting without replacement.
The total probability that we grab all Twix from the bowl is the product of these probabilities: \frac{40}{100} \cdot \frac{39}{99} \cdot \frac{38}{98}
The average score on this problem was 94%.
What is the probability you get no Twix? Leave your answer completely unsimplified, similar to the answer choices for part (a).
Answer: \dfrac{60}{100} \cdot \dfrac{59}{99} \cdot \dfrac{58}{98}
We need to find the probability that we get no Twix among the three candies selected from the bowl. We know that two candies are not Twix in our bowl (M&Ms and Kitkats). Since we are selecting three times from the same bowl, we know that we are selecting without replacement.
The total probability that we grab no Twix from the bowl is the product of these probabilities: \frac{60}{100} \cdot \frac{59}{99} \cdot \frac{58}{98}
The average score on this problem was 81%.
Let a be your answer to part (a) and let b be your answer to part (b). Write a mathematical expression in terms of a and/or b that evaluates to the probability of getting some Twix and some non-Twix candy from this house.
Answer: 1 - a - b or 1 - (a + b)
The case where we get some Twix and some non-Twix occurs can also be thought of as the case when we DO NOT get either all Twix OR all non-Twix. In 6.1 we calculated the probability of getting all Twix as a and in 6.2 we calculated the probability of getting all non-Twix as b. Therefore the probability of getting either all Twix OR all non-Twix is equal to a + b. However, we are looking for the probability that this does not happen, meaning our answer is 1 - (a + b).
The average score on this problem was 30%.
Suppose that for each word in the English language, Matt has a 70\% chance of finding it difficult. Suppose also that the difficulty of each word is independent of the difficulty of any other word.
For all parts of this problem, give your answer as a decimal number or as an unsimplified mathematical expression.
If Matt reads a sentence of 10 words, what is the probability that he finds every word difficult?
Answer: (0.7)^{10}
Each word is independent, so the probability of finding 10 straight words difficult is just the probability of finding any particular word difficult to the tenth power.
The average score on this problem was 89%.
If Matt reads a sentence of 10 words, what is the probability that he finds at least one word difficult?
Answer: 1 - (0.3)^{10}
This is a problem where it’s easier to find the probability that the given event doesn’t happen. The only way this would not happen is if Matt finds absolutely none of the words difficult. That would have a probability of (1-0.7)^{10}, and our answer is going to be 1 minus that.
The average score on this problem was 62%.
Now suppose that Ryan finds the English language slightly more difficult, as it’s not his first language:
For any given word, what is the probability that at least one of Matt and Ryan finds it difficult?
Answer: 1 - 0.3 * 0.5 = 0.85
For this problem its easier to find the probability that this doesn’t happen. The only way this would not happen would be if both Matt and Ryan don’t find the word difficult. For Matt, that happens with probability 0.3. And then given that Matt doesn’t find the word difficult, Ryan has a 0.5 probability of not finding the word difficult. Multiplying those two probabilities and subtracting from 1 gives us our answer.
The average score on this problem was 34%.
What is the probability that for every word in a sentence of 10 words, exactly one of Matt and Ryan finds the word difficult?
Answer: (0.7 * 0.1 + 0.3 * 0.5)^{10} = (0.22)^{10}
Since each word is independent, we only need to find the probability that for one particular word either Matt or Ryan finds it difficult but not both, and then we can take that probability to the power of 10. The first case is that Matt finds a word difficult but Ryan doesn’t. The first part happens with probability 0.7, and given that Matt found the word difficult, the second part happens with probability 0.1. We multiply those to get one part of our sum. The other case is that Matt doesn’t find a word difficult but Ryan does. The first part happens with probability 0.3, and given that, the second part happens with probability 0.5. Multiplying these two gives us the second part of our sum.
The average score on this problem was 17%.
The HAUGA bedroom furniture set includes two items, a bed frame and a bedside table. Suppose the amount of time it takes someone to assemble the bed frame is a random quantity drawn from the probability distribution below.
| Time to assemble bed frame | Probability |
|---|---|
| 10 minutes | 0.1 |
| 20 minutes | 0.4 |
| 30 minutes | 0.5 |
Similarly, the time it takes someone to assemble the bedside table is a random quantity, independent of the time it takes them to assemble the bed frame, drawn from the probability distribution below.
| Time to assemble bedside table | Probability |
|---|---|
| 30 minutes | 0.3 |
| 40 minutes | 0.4 |
| 50 minutes | 0.3 |
What is the probability that Stella assembles the bed frame in 10 minutes if we know it took her less than 30 minutes to assemble? Give your answer as a decimal between 0 and 1.
Answer: 0.2
We want to find the probability that Stella assembles the bed frame in 10 minutes, given that she assembles it in less than 30 minutes. The multiplication rule can be rearranged to find the conditional probability of one event given another.
\begin{aligned} P(A \text{ and } B) &= P(A \text{ given } B)*P(B)\\ P(A \text{ given } B) &= \frac{P(A \text{ and } B)}{P(B)} \end{aligned}
Let’s, therefore, define events A and B as follows:
Since 10 minutes is less than 30 minutes, A \text{ and } B is the same as A in this case. Therefore, P(A \text{ and } B) = P(A) = 0.1.
Since there are only two ways to complete the bed frame in less than 30 minutes (10 minutes or 20 minutes), it is straightforward to find P(B) using the addition rule P(B) = 0.1 + 0.4. The addition rule can be used here because assembling the bed frame in 10 minutes and assembling the bed frame in 20 minutes are mutually exclusive. We could alternatively find P(B) using the complement rule, since the only way not to complete the bed frame in less than 30 minutes is to complete it in exactly 30 minutes, which happens with a probability of 0.5. We’d get the same answer, P(B) = 1 - 0.5 = 0.5.
Plugging these numbers in gives our answer.
\begin{aligned} P(A \text{ given } B) &= \frac{P(A \text{ and } B)}{P(B)}\\ &= \frac{0.1}{0.5}\\ &= 0.2 \end{aligned}
The average score on this problem was 72%.
What is the probability that Ryland assembles the bedside table in 40 minutes if we know that it took him 30 minutes to assemble the bed frame? Give your answer as a decimal between 0 and 1
Answer: 0.4
We are told that the time it takes someone to assemble the bedside table is a random quantity, independent of the time it takes them to assemble the bed frame. Therefore we can disregard the information about the time it took him to assemble the bed frame and read directly from the probability distribution that his probability of assembling the bedside table in 40 minutes is 0.4.
The average score on this problem was 82%.
What is the probability that Jin assembles the complete HAUGA set in at most 60 minutes? Give your answer as a decimal between 0 and 1.
Answer: 0.53
There are several different ways for the total assembly time to take at most 60 minutes:
Using the multiplication rule, these probabilities are:
Finally, adding them up because they represent mutually exclusive cases, we get 0.1+0.28+0.15 = 0.53.
The average score on this problem was 58%.
You’re definitely going to Sun God 2022, but you don’t want to go alone! Fortunately, you have n friends who promise to go with you. Unfortunately, your friends are somewhat flaky, and each has a probability p of actually going (independent of all others). What is the probability that you wind up going alone? Give your answer in terms of p and n.
Answer: (1-p)^n
If you go alone, it means all of your friends failed to come. We can think of this as an and condition in order to use multiplication. The condition is: your first friend doesn’t come and your second friend doesn’t come, and so on. The probability of any individual friend not coming is 1-p, so the probability of all your friends not coming is (1-p)^n.
The average score on this problem was 76%.
In past Sun God festivals, sometimes artists that were part of the lineup have failed to show up! Let’s say there are n artists scheduled for Sun God 2022, and each artist has a probability p of showing up (independent of all others). What is the probability that the number of artists that show up is less than n, meaning somebody no-shows? Give your answer in terms of p and n.
Answer: 1-p^n
It’s actually easier to figure out the opposite event. The opposite of somebody no-showing is everybody shows up. This is easier to calculate because we can think of it as an and condition: the first artist shows up and the second artist shows up, and so on. That means we just multiply probabilities. Therefore, the probability of all artists showing up is p^n and the probability of some artist not showing up is 1-p^n.
The average score on this problem was 73%.
The four most common majors among students in DSC 10 this quarter are
"MA30" (Mathematics - Computer Science),
"EN30" (Business Economics), "EN25"
(Economics), and "CG35" (Cognitive Science with a
Specialization in Machine Learning and Neural Computation). We’ll call
these four majors “popular majors".
There are 80 students in DSC 10 with a popular major. The distribution of popular majors is given in the bar chart below.
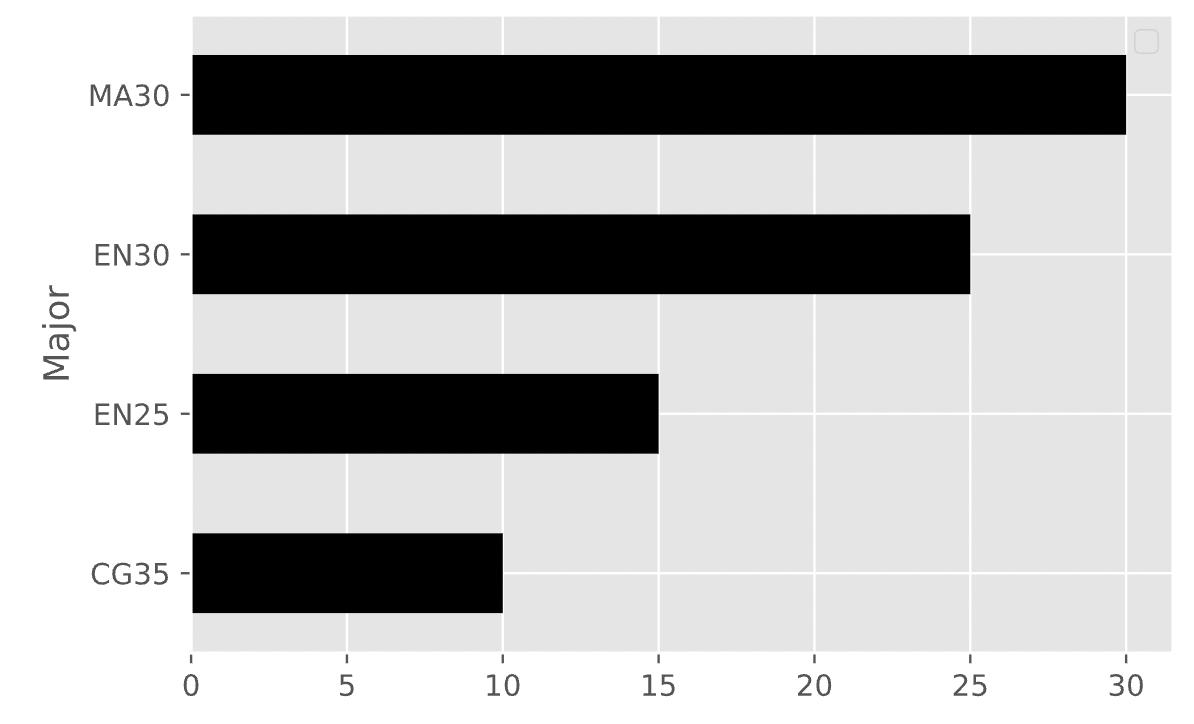
Fill in the blank below so that the expression outputs the bar chart above.
(survey
.groupby("Major").count()
.sort_values("College")
.take(____)
.get("Section")
.plot(kind="barh")
)What goes in the blank?
Answer: [-4, -3. -2, -1]
Let’s break down the code line by line:
.groupby("Major") will group the survey DataFrame by
the "Major" column..count() will count the number of students in each
major..sort_values("College") sort these counts in ascending
order using the "College" column (which now contains
counts)..take([-4, -3. -2, -1]) will take the last 4 rows of
the DataFrame, which will correspond to the 4 most common majors..get("Section") get the "Section" column,
which also contains counts..plot(kind="barh") will plot these counts in a
horizontal bar chart.The argument we give to take is
[-4, -3, -2, -1], because that will give us back a
DataFrame corresponding to the counts of the 4 most common majors, with
the most common major ("MA30") at the bottom. We want the
most common major at the bottom of the Series that
.plot(kind="barh") is called on because the bottom row will
correspond to the top bar – remember, kind="barh" plots one
bar per row, but in reverse order.
The average score on this problem was 4%.
Suppose we select two students in popular majors at
random with replacement. What is the probability that both have
"EN" in their major code? Give your answer in the form of a
simplified fraction.
Answer: \frac{1}{4}
"EN" in their major code is
the sum of "EN30" and "EN25" students: 25 + 15 = 40The probability that a single student chosen at random from the
popular majors has "EN" in their major code is number of
"EN" majors divided by total number of popular majors.
P(\text{one has ``EN"}) = \frac{40}{80} = \frac{1}{2}
Since the students are chosen with replacement, the probabilities
remain consistent for each draw. So the probability that both randomly
chosen students (with replacement) have "EN" in their major
code is
P(\text{both have ``EN"}) = P(\text{one has ``EN"}) \cdot P(\text{one has ``EN"}) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}
The average score on this problem was 61%.
Suppose we select two students in popular majors at
random with replacement. What is the probability that we select one
"CG35" major and one "MA30" major (in any
order)?
\frac{1}{2}
\frac{3}{4}
\frac{3}{8}
\frac{3}{16}
\frac{3}{32}
\frac{3}{64}
Answer: \frac{3}{32}
"CG35" major first and
then one "MA30" major is: \frac{10}{80} \cdot \frac{30}{80} = \frac{1}{8} \cdot \frac{3}{8} = \frac{3}{64}"MA30" major first and
then one "CG35" major is: \frac{30}{80} \cdot \frac{10}{80} = \frac{3}{8} \cdot \frac{1}{8} = \frac{3}{64}Since the two events are mutually exclusive (they cannot both
happen), we sum their probabilities to get the combined probability of
the event occurring in any order:
P(\text{one ``CG35" and one
``MA30"}) = P(\text{``CG35" then ``MA30" OR ``MA30"
then ``CG35"}) = P(\text{``CG35 then ``MA30"}) +
P(\text{``MA30" then ``CG35"}) = \frac{3}{64} + \frac{3}{64} =
\frac{6}{64} = \frac{3}{32}
The average score on this problem was 18%.
Suppose we select k
students in popular majors at random with replacement. What is the
probability that we select at least one "CG35" major?
\frac{7}{8}
\frac{7^k}{8^k}
\frac{1}{7^k}
\frac{1}{8^k}
\frac{8^k - 7^k}{7^k}
\frac{8^k - 7^k}{8^k}
Answer: \frac{8^k - 7^k}{8^k}
Of the 80 students in popular majors, 10 are in "CG35".
To determine the likelihood of selecting at least one
"CG35" major out of k random draws with replacement, we
first find the probability of not drawing a "CG35" major in
all k attempts by
following the steps below:
The probability of not selecting a "CG35" major in
one draw is 1 - \frac{10}{80} = 1 - \frac{1}{8} = \frac{7}{8}
The probability of not selecting a "CG35" major in
k draws is, then,
\frac{7^k}{8^k}, since each draw is
independent.
Now, by subtracting this probability from 1, we get the probability
of drawing at least one "CG35" major in those k attempts. So, the probability of
selecting at least one "CG35" major in k attempts is 1 - \frac{7^k}{8^k} = \frac{8^k}{8^k} -
\frac{7^k}{8^k} = \frac{8^k - 7^k}{8^k}
The average score on this problem was 58%.
Next year, six of the DSC tutors (Kathleen, Sophia, Kate, Ashley, Claire, and Vivian) want to rent a 3-bedroom apartment together. Each person will have a single roommate with whom they’ll share a bedroom. Each person will have a single roommate with whom they’ll share a bedroom. They determine the bedroom assignments randomly such that each possible arrangement is equally likely.
For both questions below, give your answer as a simplified fraction or exact decimal.
Hint: Both answers can be expressed in the form \frac{1}{k} for an integer value of k.
What is the probability that Kathleen and Sophia are roommates?
Hint: Think about the problem from the perspective of Kathleen.
Answer: \displaystyle\frac{1}{5}
From Kathleen’s perspective, there are 5 tutors that are equally likely to become her roommate. So, the probability that Sophia ends up being Kathleen’s roommate is \displaystyle\frac{1}{5}.
The average score on this problem was 90%.
What is the probability that the bedroom assignments are the following: Kathleen with Sophia, Kate with Ashley, and Claire with Vivian?
Answer: \frac{1}{15}
In order to get this combination of roommates, we can use similar logic as before. From Kathleen’s perspective, there are 5 tutors that are equally likely to become her roommate. So, the probability that Sophia ends up being Kathleen’s roommate is \displaystyle\frac{1}{5}. From there, we can view the situation from Kate’s perspective; Kate sees that there are 3 potential roommates left (Ashley, Claire, Vivian). So, the probability that Sophia ends up being Kathleen’s roommate (given Kathleen and Sophia are together) is \displaystyle\frac{1}{3}. After Kate chooses her roommate, Claire and Vivian end up together by process of elimination. We can multiply these two probabilities to recieve: \displaystyle\frac{1}{5} \cdot \displaystyle\frac{1}{5} = \displaystyle\frac{1}{15}.
The average score on this problem was 47%.
Oh no! A monkey has grabbed your phone and is dialing a phone number by randomly pressing buttons on the keypad, such that each button pressed is equally likely to be any of ten digits 0 through 9.
The monkey managed to dial a ten-digit number and call that number.
What is the probability that the monkey calls one of your contacts? Give
your answer as a Python expression, using the DataFrame
contacts.
Answer:
(contacts.shape[0])/(10**10)
contacts.shape[0]: retrieves the number of rows in the
contacts DataFrame, representing the total number of phone numbers you
have stored in your contacts.10**10: Since the phone number consists of ten digits,
and each digit can be any number from 0 to 9, there are a total of
10**10 possible ten-digit numbers.Given that each digit pressed is equally likely and independent of
others, the likelihood of hitting a specific number from your contacts
by random chance is simply the count of your contacts divided by the
total number of possible combinations (which is
10**10).
The average score on this problem was 43%.
Now, your cat is stepping carefully across the keypad of your phone, pressing 10 buttons. Each button is sampled randomly without replacement from the digits 0 through 9.
You catch your cat in the act of dialing, when the cat has already dialed 987-654. Based on this information, what is the probability that the cat dials your friend Calvin’s number, 987-654-3210? Give your answer as an unsimplified mathematical expression.
Answer: \dfrac{1}{4 \cdot 3 \cdot 2 \cdot 1}
The cat has already dialed “987-654”. Since the first six digits are fixed and chosen without replacement, the only remaining digits to be dialed are 3, 2, 1, and 0. The sequence “3210” must be dialed in that exact order from the remaining digits.
The product of these probabilities gives \dfrac{1}{4 \cdot 3 \cdot 2 \cdot 1}, representing the likelihood of this specific sequence occurring.
The average score on this problem was 55%.
As we saw in the last problem, children aged 12 to 18 (inclusive) have tickets entered into a drawing at the reaping. 12-year-olds have one ticket, 13-year-olds have two tickets, 14-year-olds have three tickets, and so on, gaining one ticket per year of age.
In this problem, we’ll look at the ages of all boys from District 3 and determine the probability that a boy of a certain age is selected in the drawing.
Suppose that there are only five boys from District 3 and their ages are as follows (in no particular order):
17, 12, 15, 14, 12.
Determine the probability that a 17-year-old is selected in the drawing.
Give your answer as an unsimplified fraction where the numerator is the number of tickets corresponding to a 17-year-old and the denominator is the total number of tickets.
Answer: 6/15
A short cut we can use to check how many tickets each kid gets is just taking their age and subtracting 11. If we do this for all of the listed kids given their ages, we get a total of 15 tickets. Furthermore, using our shortcut, the number of tickets allocated to the 17 year old would be 6. Thus, the unsimplified fraction is 6/15.
The average score on this problem was 88%.
Now, we’ll solve the problem more generally. Fill in the blanks below
to define a function pick_prob that takes as input an array
containing the ages of all boys in District 3, and a single age between 12 and 18
(inclusive). The function should return the probability of randomly
selecting a boy of that age during the reaping.
def pick_prob(ages, one_age):
age_tickets = __(a)__
total_tickets = __(b)__
return age_tickets / total_ticketsAnswer:
(a):
sum((ages == one_age) * (one_age - 11))
(b): (ages - 11).sum()
In part a we find how many tickets come from boys of the given age by taking the sum of all matches within the input and multiplied by the corresponding ticket value for that age.
In part b, to find the total number of tickets, we take all values in the input and calculate the corresponding number of tickets then add them all up.
The average score on this problem was 70%.
Using pick_prob, write one line of code that evaluates
to the probability that a 14-year-old
boy is not chosen during the reaping if the boys in
District 3 are aged 12, 14,
14, 15, 17, and
18.
Answer:
1 - pick_prob(np.array([12, 14, 14, 15, 17, 18]), 14)
To solve this problem we can simply take the complement of the
probability that we do select a 14-year-old boy during the reaping. With the
given ages of the boys in the problem statement, we can use the function
we defined above to calculate this. As a result, to arrive at our answer
we can simply take
1 - pick_prob(np.array([12, 14, 14, 15, 17, 18]), 14).
The average score on this problem was 88%.
Most imported goods are transported to the US in shipping containers. The table to below shows the probability that a randomly selected shipping container comes from a given location (continent or country). Note that the probability for each continent is the sum of the probabilities for each country in that continent.
For all parts of this question, you can leave your answer as an unsimplified mathematical expression.
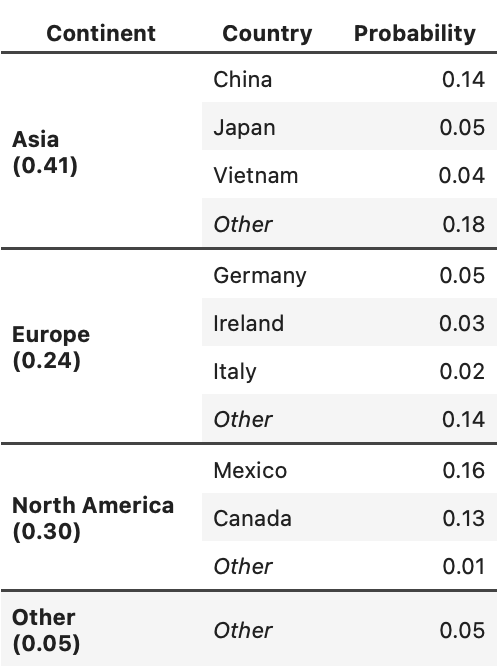
Suppose you randomly select one shipping container. You are told that it comes from Asia but not from Japan. What is the probability that it comes from China?
Answer: \frac{0.14}{0.36}=\frac{7}{18}
The average score on this problem was 53%.
True or False: Selecting a shipping container from Vietnam and selecting a shipping container from Ireland are independent events.
True
False
Answer: False
If two events A and B are independent then P(A and B) = P(A)P(B). In this question we can define A as “selecting a shipping container from Vietnam” and B as “selecting a shipping container from Ireland”. Therefore (A and B) would be “selecting a (single) shipping container from both Vietnam and Ireland”. Since that is impossible, P(A and B) = 0 while P(A)P(B) = 0.012. Therefore these two events are not independent.
The average score on this problem was 32%.
Suppose you randomly select two shipping containers, with replacement. What is the probability that exactly one comes from Germany and the other comes from somewhere in North America?
Answer: 0.03
The probability of selecting Germany as the first shipping container is 0.05. Given that Germany is selected first, the probability that the second container is from the United States is 0.3. However, since the order of the containers can be swapped, you need to multiply by 2 to account for both possible arrangements.
The average score on this problem was 46%.
Suppose you randomly select three shipping containers, with replacement. What is the probability that none of them comes from Asia?
Answer: 0.59^{3}
There are three important pieces of information to take note:
This means that we have three trials with replacement, all looking for the same outcome. Given that the probability of a shipping container is .41, we know that the complement is:
\text{Not from Asia} = 1 - .41 \text{Not from Asia} = .59
To get this outcome three times with replacement, we can do the following:
.59 \times .59 \times .59
\therefore .59^3
The average score on this problem was 42%.
There’s been an expansion of Collegiate Mario Kart across the
country, so to determine a champion, we’d like to set up a bracket for a
Mario Kart tournament and fill it with four college teams from
bigkart. We won’t display bigkart for this
question, but assume it’s a larger version of kart: there
are 50 rows in bigkart, and thus 50 teams. Selection is
performed uniformly at random, so that each team has the same chance of
being selected. Please leave your answers in
unsimplified form: answers of the form (\frac{3}{4}) \cdot (\frac{2}{3}) or \left[1 - (\frac{1}{2})^4\right] are
preferred.
Assume we populate our tournament by randomly selecting four teams
from bigkart with replacement. What is the
probability there are no duplicates among the four teams selected for
the tournament? Do not simplify your answer.
Answer: \frac{1}{1} \cdot \frac{49}{50} \cdot \frac{48}{50} \cdot \frac{47}{50}
We need to find the probability that there are no duplicates among
the four teams selected for the tournament from bigkart
with replacement. Since we are selecting four times, we
want each selected team to be unique.
The total probability that there are no duplicates among the four teams selected is the product of these probabilities: \frac{1}{1} \cdot \frac{49}{50} \cdot \frac{48}{50} \cdot \frac{47}{50}
The average score on this problem was 45%.
Now, assume we populate our tournament by randomly selecting four
teams from bigkart without replacement.
Additionally, assume 30 are from Division 1 and 20 teams are from
Division 2. What is the probability that there is at least one Division
2 team among the four teams selected for the tournament? Do not simplify
your answer.
Answer: 1 - \frac{30}{50} \cdot \frac{29}{49} \cdot \frac{28}{48} \cdot \frac{27}{47}
We are selecting four teams from bigkart without
replacement, and we want to calculate the probability that
at least one Division 2 team is selected, which
represented as P(A). We know that there are 30 Division 1 teams and 20
Division 2 teams.
First calculating the complement probability, P(Ac) which is the probability that all four teams are from Division 1.
The probability that all four teams are from Division 1 is: \frac{30}{50} \cdot \frac{29}{49} \cdot \frac{28}{48} \cdot \frac{27}{47}
To find the probability of at least one Division 2 team being selected, we use P(A) = 1 - P(Ac): 1 - \frac{30}{50} \cdot \frac{29}{49} \cdot \frac{28}{48} \cdot \frac{27}{47}
The average score on this problem was 57%.
True or False: If you roll two dice, the probability of rolling two fives is the same as the probability of rolling a six and a three.
Answer: False
The probability of rolling two fives can be found with 1/6 * 1/6 = 1/36. The probability of rolling a six and a three can be found with 2/6 (can roll either a 3 or 6) * 1/6 (roll a different side form 3 or 6, depending on what you rolled first) = 1/18. Therefore, the probabilities are not the same.
The average score on this problem was 33%.
You generate a three-digit number by randomly choosing each digit to be a number 0 through 9, inclusive. Each digit is equally likely to be chosen.
What is the probability you produce the number 027? Give your answer as a decimal number between 0 and 1 with no rounding.
Answer: 0.001
There is a \frac{1}{10} chance that we get 0 as the first random number, a \frac{1}{10} chance that we get 2 as the second random number, and a \frac{1}{10} chance that we get 7 as the third random number. The probability of all of these events happening is \frac{1}{10}*\frac{1}{10}*\frac{1}{10} = 0.001.
Another way to do this problem is to think about the possible outcomes. Any number from 000 to 999 is possible and all are equally likely. Since there are 1000 possible outcomes and the number 027 is just one of the possible outcomes, the probability of getting this outcome is \frac{1}{1000} = 0.001.
The average score on this problem was 92%.
What is the probability you produce a number with an odd digit in the middle position? For example, 250. Give your answer as a decimal number between 0 and 1 with no rounding.
Answer: 0.5
Because the values of the left and right positions are not important to us, think of the middle position only. When selecting a random number to go here, we are choosing randomly from the numbers 0 through 9. Since 5 of these numbers are odd (1, 3, 5, 7, 9), the probability of getting an odd number is \frac{5}{10} = 0.5.
The average score on this problem was 78%.
What is the probability you produce a number with a 7 in it somewhere? Give your answer as a decimal number between 0 and 1 with no rounding.
Answer: 0.271
It’s easier to calculate the probability that the number has no 7 in it, and then subtract this probability from 1. To solve this problem directly, we’d have to consider cases where 7 appeared multiple times, which would be more complicated.
The probability that the resulting number has no 7 is \frac{9}{10}*\frac{9}{10}*\frac{9}{10} = 0.729 because in each of the three positions, there is a \frac{9}{10} chance of selecting something other than a 7. Therefore, the probability that the number has a 7 is 1 - 0.729 = 0.271.
The average score on this problem was 69%.
Recall, plum has 31 rows.
Consider the function df_choice, defined below.
def df_choice(df):
return df[np.random.choice([True, False], df.shape[0], replace=True)]Suppose we call df_choice(plum) once. What is the
probability that the result is an empty DataFrame?
0
1
\frac{1}{2^{25}}
\frac{1}{2^{30}}
\frac{1}{2^{31}}
\frac{2^{31} - 1}{2^{31}}
\frac{31}{2^{30}}
\frac{31}{2^{31}}
None of the above
Answer: \frac{1}{2^{31}}
First, let’s understand what df_choice does. It takes in
one input, df. The line
np.random.choice([True, False], df.shape[0], replace=True)
evaluates to an array such that:
df (so if df has 31 rows, the output array
will have length 31)True or
False, since the sequence we are selecting from is
[True, False] and we are selecting with replacementSo
np.random.choice([True, False], df.shape[0], replace=True)
is an array the same length as df, with each element
randomly set to True or False. Note that there
is a \frac{1}{2} chance the first
element is True, a \frac{1}{2} chance the second element is
True, and so on.
Then,
df[np.random.choice([True, False], df.shape[0], replace=True)]
is using Boolean indexing to keep only the rows in df where
the array
np.random.choice([True, False], df.shape[0], replace=True)
contains the value True. So, the function
df_choice returns a DataFrame containing
somewhere between 0 and df.shape[0] rows. Note that there
is a \frac{1}{2} chance that the new
DataFrame contains the first row from df, a \frac{1}{2} chance that the new DataFrame
contains the second row from df, and so on.
In this question, the only input ever given to df_choice
is plum, which has 31 rows.
In this subpart, we’re asked for the probability that
df_choice(plum) is an empty DataFrame. There are 31 rows,
and each of them have a \frac{1}{2}
chance of being included in the output, and so a \frac{1}{2} chance of being missing. So, the
chance that they are all missing is:
\begin{aligned} P(\text{empty DataFrame}) &= P(\text{all rows missing}) \\ &= P(\text{row 0 missing and row 1 missing and ... and row 30 missing}) \\ &= P(\text{row 0 missing}) \cdot P(\text{row 1 missing}) \cdot ... \cdot P(\text{row 30 missing}) \\ &= \frac{1}{2} \cdot \frac{1}{2} \cdot ... \cdot \frac{1}{2} \\ &= \boxed{\frac{1}{2^{31}}} \end{aligned}
The average score on this problem was 83%.
Suppose we call df_choice(plum) once. What is the
probability that the result is a DataFrame with 30 rows?
0
1
\frac{1}{2^{25}}
\frac{1}{2^{30}}
\frac{1}{2^{31}}
\frac{2^{31} - 1}{2^{31}}
\frac{31}{2^{30}}
\frac{31}{2^{31}}
None of the above
Answer: \frac{31}{2^{31}}
In order for the resulting DataFrame to have 30 rows, exactly 1 row must be missing, and the other 30 must be present.
To start, let’s consider one row in particular, say, row 7. The probability that row 7 is missing is \frac{1}{2}, and the probability that rows 0 through 6 and 8 through 30 are all present is \frac{1}{2} \cdot \frac{1}{2} \cdot ... \cdot \frac{1}{2} = \frac{1}{2^{30}} using the logic from the previous subpart. So, the probability that row 7 is missing AND all other rows are present is \frac{1}{2} \cdot \frac{1}{2^{30}} = \frac{1}{2^{31}}.
Then, in order for there to be 30 rows, either row 0 must be missing, or row 1 must be missing, and so on:
\begin{aligned} P(\text{exactly one row missing}) &= P(\text{only row 0 is missing or only row 1 is missing or ... or only row 30 is missing}) \\ &= P(\text{only row 0 is missing}) + P(\text{only row 1 is missing}) + ... + P(\text{only row 30 is missing}) \\ &= \frac{1}{2^{31}} + \frac{1}{2^{31}} + ... + \frac{1}{2^{31}} \\ &= \boxed{\frac{31}{2^{31}}} \end{aligned}
The average score on this problem was 48%.
Suppose we call df_choice(plum) once.
True or False: The probability that the result is a
DataFrame that consists of just row 0 from
plum (and no other rows) is equal to the probability you
computed in the first subpart of this problem.
True
False
Answer: True
An important realization to make is that all subsets
of the rows in plum are equally likely to be returned by
df_choice(plum), and they all have probability \frac{1}{2^{31}}. For instance, one subset of
plum is the subset where rows 2, 5, 8, and 30 are missing,
and the rest are all present. The probability that this subset is
returned by df_choice(plum) is \frac{1}{2^{31}}.
This is true because for each individual row, the probability that it is present or missing is the same – \frac{1}{2} – so the probability of any subset is a product of 31 \frac{1}{2}s, which is \frac{1}{2^{31}}. (The answer to the previous subpart was not \frac{1}{2^{31}} because it was asking about multiple subsets – the subset where only row 0 was missing, and the subset where only row 1 was missing, and so on).
So, the probability that df_choice(plum) consists of
just row 0 is \frac{1}{2^{31}}, and
this is the same as the answer to the first subpart (\frac{1}{2^{31}}); in both situations, we are
calculating the probability of one specific subset.
The average score on this problem was 63%.
Suppose we call df_choice(plum) once.
What is the probability that the resulting DataFrame has 0 rows, or 1 row, or 30 rows, or 31 rows?
0
1
\frac{1}{2^{25}}
\frac{1}{2^{30}}
\frac{1}{2^{31}}
\frac{2^{31} - 1}{2^{31}}
\frac{31}{2^{30}}
\frac{31}{2^{31}}
None of the above
Answer: \frac{1}{2^{25}}
Here, we’re not being asked for the probability of one specific subset (like the subset containing just row 0); rather, we’re being asked for the probability of various different subsets, so our calculation will be a bit more involved.
We can break our problem down into four pieces. We can find the probability that there are 0 rows, 1 row, 30 rows, and 31 rows individually, and add these probabilities up, since only one of them can happen at a time (it’s impossible for a DataFrame to have both 1 and 30 rows at the same time; these events are “mutually exclusive”). It turns out we’ve already calculated two of these probabilities:
The other two possibilities are symmetric with the above two!
Putting it all together, we have:
\begin{aligned} P(\text{number of returned rows is 0, 1, 30, or 31}) &= P(\text{0 rows are returned}) + P(\text{1 row is returned}) + P(\text{30 rows are returned}) + P(\text{31 rows are returned}) \\ &= \frac{1}{2^{31}} + \frac{31}{2^{31}} + \frac{31}{2^{31}} + \frac{1}{2^{31}} \\ &= \frac{1 + 31 + 31 + 1}{2^{31}} \\ &= \frac{64}{2^{31}} \\ &= \frac{2^6}{2^{31}} \\ &= \frac{1}{2^{31 - 6}} \\ &= \boxed{\frac{1}{2^{25}}} \end{aligned}
The average score on this problem was 35%.
Suppose you have a DataFrame called plum with 31
rows.
Consider the function df_choice, defined below.
def df_choice(df):
return df[np.random.choice([True, False], df.shape[0], replace=True)]Suppose we call df_choice(plum) once. What is the
probability that the result is an empty DataFrame?
0
1
\frac{1}{2^{25}}
\frac{1}{2^{30}}
\frac{1}{2^{31}}
\frac{2^{31} - 1}{2^{31}}
\frac{31}{2^{30}}
\frac{31}{2^{31}}
None of the above
Answer: \frac{1}{2^{31}}
First, let’s understand what df_choice does. It takes in
one input, df. The line
np.random.choice([True, False], df.shape[0], replace=True)
evaluates to an array such that:
df (so if df has 31 rows, the output array
will have length 31)True or
False, since the sequence we are selecting from is
[True, False] and we are selecting with replacementSo
np.random.choice([True, False], df.shape[0], replace=True)
is an array the same length as df, with each element
randomly set to True or False. Note that there
is a \frac{1}{2} chance the first
element is True, a \frac{1}{2} chance the second element is
True, and so on.
Then,
df[np.random.choice([True, False], df.shape[0], replace=True)]
is using Boolean indexing to keep only the rows in df where
the array
np.random.choice([True, False], df.shape[0], replace=True)
contains the value True. So, the function
df_choice returns a DataFrame containing
somewhere between 0 and df.shape[0] rows. Note that there
is a \frac{1}{2} chance that the new
DataFrame contains the first row from df, a \frac{1}{2} chance that the new DataFrame
contains the second row from df, and so on.
In this question, the only input ever given to df_choice
is plum, which has 31 rows.
In this subpart, we’re asked for the probability that
df_choice(plum) is an empty DataFrame. There are 31 rows,
and each of them have a \frac{1}{2}
chance of being included in the output, and so a \frac{1}{2} chance of being missing. So, the
chance that they are all missing is:
\begin{aligned} P(\text{empty DataFrame}) &= P(\text{all rows missing}) \\ &= P(\text{row 0 missing and row 1 missing and ... and row 30 missing}) \\ &= P(\text{row 0 missing}) \cdot P(\text{row 1 missing}) \cdot ... \cdot P(\text{row 30 missing}) \\ &= \frac{1}{2} \cdot \frac{1}{2} \cdot ... \cdot \frac{1}{2} \\ &= \boxed{\frac{1}{2^{31}}} \end{aligned}
Suppose we call df_choice(plum) once. What is the
probability that the result is a DataFrame with 30 rows?
0
1
\frac{1}{2^{25}}
\frac{1}{2^{30}}
\frac{1}{2^{31}}
\frac{2^{31} - 1}{2^{31}}
\frac{31}{2^{30}}
\frac{31}{2^{31}}
None of the above
Answer: \frac{31}{2^{31}}
In order for the resulting DataFrame to have 30 rows, exactly 1 row must be missing, and the other 30 must be present.
To start, let’s consider one row in particular, say, row 7. The probability that row 7 is missing is \frac{1}{2}, and the probability that rows 0 through 6 and 8 through 30 are all present is \frac{1}{2} \cdot \frac{1}{2} \cdot ... \cdot \frac{1}{2} = \frac{1}{2^{30}} using the logic from the previous subpart. So, the probability that row 7 is missing AND all other rows are present is \frac{1}{2} \cdot \frac{1}{2^{30}} = \frac{1}{2^{31}}.
Then, in order for there to be 30 rows, either row 0 must be missing, or row 1 must be missing, and so on:
\begin{aligned} P(\text{exactly one row missing}) &= P(\text{only row 0 is missing or only row 1 is missing or ... or only row 30 is missing}) \\ &= P(\text{only row 0 is missing}) + P(\text{only row 1 is missing}) + ... + P(\text{only row 30 is missing}) \\ &= \frac{1}{2^{31}} + \frac{1}{2^{31}} + ... + \frac{1}{2^{31}} \\ &= \boxed{\frac{31}{2^{31}}} \end{aligned}
Suppose we call df_choice(plum) once.
True or False: The probability that the result is a
DataFrame that consists of just row 0 from
plum (and no other rows) is equal to the probability you
computed in the first subpart of this problem.
True
False
Answer: True
An important realization to make is that all subsets
of the rows in plum are equally likely to be returned by
df_choice(plum), and they all have probability \frac{1}{2^{31}}. For instance, one subset of
plum is the subset where rows 2, 5, 8, and 30 are missing,
and the rest are all present. The probability that this subset is
returned by df_choice(plum) is \frac{1}{2^{31}}.
This is true because for each individual row, the probability that it is present or missing is the same – \frac{1}{2} – so the probability of any subset is a product of 31 \frac{1}{2}s, which is \frac{1}{2^{31}}. (The answer to the previous subpart was not \frac{1}{2^{31}} because it was asking about multiple subsets – the subset where only row 0 was missing, and the subset where only row 1 was missing, and so on).
So, the probability that df_choice(plum) consists of
just row 0 is \frac{1}{2^{31}}, and
this is the same as the answer to the first subpart (\frac{1}{2^{31}}); in both situations, we are
calculating the probability of one specific subset.
Suppose we call df_choice(plum) once.
What is the probability that the resulting DataFrame has 0 rows, or 1 row, or 30 rows, or 31 rows?
0
1
\frac{1}{2^{25}}
\frac{1}{2^{30}}
\frac{1}{2^{31}}
\frac{2^{31} - 1}{2^{31}}
\frac{31}{2^{30}}
\frac{31}{2^{31}}
None of the above
Answer: \frac{1}{2^{25}}
Here, we’re not being asked for the probability of one specific subset (like the subset containing just row 0); rather, we’re being asked for the probability of various different subsets, so our calculation will be a bit more involved.
We can break our problem down into four pieces. We can find the probability that there are 0 rows, 1 row, 30 rows, and 31 rows individually, and add these probabilities up, since only one of them can happen at a time (it’s impossible for a DataFrame to have both 1 and 30 rows at the same time; these events are “mutually exclusive”). It turns out we’ve already calculated two of these probabilities:
The other two possibilities are symmetric with the above two!
Putting it all together, we have:
\begin{aligned} P(\text{number of returned rows is 0, 1, 30, or 31}) &= P(\text{0 rows are returned}) + P(\text{1 row is returned}) + P(\text{30 rows are returned}) + P(\text{31 rows are returned}) \\ &= \frac{1}{2^{31}} + \frac{31}{2^{31}} + \frac{31}{2^{31}} + \frac{1}{2^{31}} \\ &= \frac{1 + 31 + 31 + 1}{2^{31}} \\ &= \frac{64}{2^{31}} \\ &= \frac{2^6}{2^{31}} \\ &= \frac{1}{2^{31 - 6}} \\ &= \boxed{\frac{1}{2^{25}}} \end{aligned}
While they are not skyscrapers, New Sixth College at UCSD has four relatively tall residential buildings, which we’ll call Building A, Building B, Building C, and Building D. Suppose each building has 10 floors.
Sixth College administration decides to ease the General Education requirements for a few randomly selected students. Here’s their strategy:
Everyone on one of the four floors selected in Wave 1 has the CAT 1 requirement waived. Everyone on the one floor selected in Wave 2 has both the CAT 1 and CAT 2 requirements waived.
Billy lives on the 8th floor of Building C. What’s the probability that Billy has both the CAT 1 and CAT 2 requirements waived? Give your answer as a proportion between 0 and 1, rounded to 3 decimal places.
Answer: 0.025
In order for the 8th floor of Building C to be selected, two things need to happen:
Since both events need to occur, and both events are independent (think of selecting in each wave as drawing names from a hat), the probability that both occur is the product of the probabilities that they occur individually:
\frac{1}{10} \cdot \frac{1}{4} = \frac{1}{40} = 0.025
The average score on this problem was 80%.
What’s the probability that at least one of the top (10th) floors of all four buildings are selected in Wave 1?
Give your answer as a proportion between 0 and 1, rounded to 3 decimal places.
Answer: 0.344
Whenever we are asked to compute the probability of “at least one” occurrence of some event, it is almost always easiest to compute the complement of (i.e. “1 minus”) the probability that there are no occurrences of the event. That is the case here; as such, we need to compute the probability that none of the 10th floors are selected across all four buildings.
To compute the probability that none of the 10th floors are selected across all four buildings, we first need to find the probability that the 10th floor is not selected in just a single building. This is 1 - \frac{1}{10} = \frac{9}{10}. Then, since the selections in each building are independent of other buildings, the probability that none of the 10th floors are selected across all four buildings is \left( \frac{9}{10} \right)^4.
Lastly, the probability we are asked for is the complement of the probability we just computed. So, the probability that at least one 10th floor is selected across all four buildings is
1 - \left( 1 - \frac{1}{10} \right)^4 = 1 - \left( \frac{9}{10} \right)^4 = 1 - 0.6561 = 0.3439
This rounds to 0.344.
The average score on this problem was 64%.
Notice that "Strategy Games" and
"Thematic Games" are two of the possible domains, and that
a game can belong to multiple domains.
Define the variables strategy and thematic follows.
strategy = games.get("Domains").str.contains("Strategy Games")
thematic = games.get("Domains").str.contains("Thematic Games")What is the data type of strategy?
bool
str
Series
DataFrame
Answer: Series
strategy will give you a Series. This is
because games.get(“Domains”) will give you one column, a
Series, and then
.str.contains(“Strategy Games”) will convert those values
to True if it contains that string and False
otherwise, but it will not actually change the Series to a
DataFrame, a bool, or a str.
The average score on this problem was 81%.
Suppose we randomly select one of the "Strategy Games"
from the games DataFrame.
What is the probability that the randomly selected game is
not also one of the "Thematic Games"?
Write a single line of Python code that evaluates to this probability,
using the variables strategy and thematic in
your solution.
Note: For this question and others that require one line of code, it’s fine if you need to write your solution on multiple lines, as long as it is just one line of Python code. Please do write on multiple lines to make sure your answer fits within the box provided.
Answer:
(games[(strategy == True) & (thematic == False)].shape[0] / games[strategy == True].shape[0])
or
1 - games[strategy & thematic].shape[0] / games[strategy].shape[0]
The problem is asking us to find the probability that a selected game
from “Strategy Games” will not be in
“Thematic Games”. Recall that this is the probability that
given “Strategy Games” will it not be in
“Thematic Games”, which would look like this:
P(“Thematic Games”
Compliment|“Strategy Games”). This means the formula would
look like: (“Thematic Games” Compliment
and
“Strategy Games”)/“Strategy Games”
This means one possible solution for this would be:
(games[(strategy == True) & (thematic == False)].shape[0] / games[strategy == True].shape[0]
This solution works because we are following the formula to find the
probability of thematic complement and strategy games over the number of
times “Strategy Games” are True. Doing
games[query_condition] gives us the games
DataFrame where strategy == True and
thematic == False. Another important thing is that for
(baby)pandas we always use the keyword & and not
and. Note that we are using .shape[0] to get
the number of rows or times that True shows up for
“Strategy Games” and the number of rows or times that
False shows up for “Thematic Games”
Compliment.
Another possible strategy would be using the complement rule: Which
would be: P(“Thematic Games” Compliment) = 1 -
P(“Thematic Games”). This would lead you to an answer like:
(1 - games[strategy & thematic].shape[0]) / games[strategy].shape[0].
games[strategy & thematic].shape[0]) finds you the
probability of P(“Thematic Games”), so when plugged into
the equation above we are able to find P(“Thematic Games”
Compliment).
The average score on this problem was 43%.
Many of the games in the games DataFrame belong to more
than one domain. We want to identify the number of games that belong to
only one domain. Select all of the options below that would correctly
calculate the number of games that belong to only one domain.
Hint: Don’t make any assumptions about the possible
domains.
(games.get("Domains").str.split(" ").apply(len) == 2).sum()
(games.get("Domains").apply(len) == 1).sum()
(games[games.get("Domains").str.split(",").apply(len) == 1].groupby("Domains").count().get("Name").sum())
games[games.get("Domains").str.split(",").apply(len) == 1].shape[0]
Answer: Options 3 and 4
Let’s take a closer look at why Option 3 and Option 4 are correct.
Option 3: Option 3 first queries the
games DataFrame to only keep games with one
“Domains”.
games.get(“Domains”).str.split(“,”).apply(len) == 1 gets
the “Domains” column and splits all of them if they contain
a comma. If the value does have a comma then it will create a list. For
example let’s say the domain was
“Strategy Games”, “Thematic Games” then after doing
str.split(“,”) we would have the list:
[“Strategy Games”, “Thematic Games”]. Any row with a
list will evaluate to False. This means we are
only keeping values where there is one domain. The next
part .groupby(“Domains”).count().get(“Name”).sum() makes a
DataFrame with an index of the unique domains and the number of times
those appear. Note that all the other columns: “Name”,
“Mechanics”, “Play Time”,
“Complexity”, “Rating”, and
“BGG Rank” now evaluate to the same thing, the number of
times a unique domain appears. That means by doing
.get(“Name”).sum() we are adding up all the number of times
a unique domain appears, which would get us the number of games that
belong to only one domain.
Option 4: Option 4 starts off exactly like Option 3,
but instead of doing .groupby() it gets the number of rows
using .shape[0], which will give us the number of games
that belong to only one domain.
Option 1: Let’s step through why Option 1 is
incorrect.
games.get(“Domains”).str.split(“ ”).apply(len) == 2.sum()
gives you a Series of the “Domains” column,
then splits each domain by a space. We then get the length of that
list, check if the length is equal to 2, which would mean
there are two elements in the list, and finally get the sum
of all elements in the list who had two elements because of the split.
Remember that True evaluates to 1 and False
evaluates to 0, so we are getting the number of elements that were split
into two. It does not tell us the number of games that belong to only
one domain.
Option 2: Let’s step through why Option 2 is also
incorrect. (games.get(“Domains”).apply(len) == 1).sum()
checks to see if each element in the column “Domains” has
only one character. Remember when you apply len() to a
string then we get the number of characters in that string. This is
essentially counting the number of domains that have 1 letter. Thus, it
does not tell us the number of games that belong to only one domain.
The average score on this problem was 86%.
Hurricane forecasters use complex models to simulate hurricanes.
Suppose a forecaster simulates 10,000 hurricanes and keeps track of the
state where each hurricane made landfall in an array called
landfalls. Each element of landfalls is a
string, which is either the full name of a US state or the string
"None" if the storm did not hit land in the simulation.
The forecaster wants to use the results of their simulation to
estimate the probability that a given storm hits Georgia. Write one line
of Python code that approximates this probability, using the data in
landfalls.
Answer:
np.count_nonzero(landfalls == "Georgia") / 10000
The probability would be the number of times the storm hit Georgia
over the total number of simulated hurricanes, which is 10000. Since
each element of landfills is a string, we can use
np.count_nonzero() to give us all of the times the storm
hits Georgia in the simulation. Recall np.count_nonzero()
determines whether the elements are “truthy”, so if the String was equal
to "Georgia" then it would be counted, and otherwise would
be ignored. Then to calculate the probability we simply divide the
number of times the storm hit Georgia by 10000.
The average score on this problem was 34%.
Oh no, a hurricane is forming! Experts predict that the storm has a 45% chance of hitting Florida, a 25% chance of hitting Georgia, a 5% chance of hitting South Carolina, and a 25% chance of not making landfall at all.
Fast forward: the storm made landfall. Assuming the expert predictions were correct, what is the probability that the storm hit Georgia? Give your answer as a fully simplified fraction between 0 and 1.
Hint: The answer is not \frac{1}{4}, or 25%.
Answer:
Originally, we were unsure if the hurricane would make landfall. Now that it has our total percentage has changed: 100\% - 25\% = 75\%. Remember probability should always add up to 100%. So our new total is 75%. We can calculate the probability that a storm hits Georgia by doing: \frac{25\%}{75\%} = \frac{1}{3}.
The average score on this problem was 36%.
Birgit Fischer-Schmidt is a German canoe paddler who set many records, including being the only woman to win Olympic medals 24 years apart.
Below is a DataFrame with information about all 12 Olympic medals she has won. There are only 10 rows but 12 medals represented, because there are some years in which she won more than one medal of the same type.
Suppose we randomly select one of Birgit’s Olympic medals, and see that it is a gold medal. What is the probability that the medal was earned in the year 2000? Give your answer as a fully simplified fraction.
Answer: \frac{1}{4}
Reading the prompt we can see that we are solving for a conditional probability. Let A be the given condition that the medal is gold and let B be the event that a medal is from 2000. Looking at the DataFrame we can see that 8 total gold medals are earned (make sure you pay attention to the count column). Out of these 8 medals, 2 of them are from the year 2000. Thus, we obtain the probability \frac{2}{8} or \frac{1}{4}.
The average score on this problem was 70%.
Suppose we randomly select one of Birgit’s Olympic medals. What is the probability it is gold or earned while representing East Germany? Give your answer as a fully simplified fraction.
Answer: \frac{3}{4}
Here we can recognize that we are solving for the probability of a union of two events. Let A be the event that the medal is gold. Let B be the event that it is earned while representing East Germany. The probability formula for a union is P(A \cup B) = P(A) + P(B) - P(A \cap B). Looking at the DataFrame, we know P(A)=\frac{8}{12}, P(B)=\frac{4}{12}, and P(A \cap B)=\frac{3}{12}. Plugging all of this into the formula, we get \frac{8}{12}+\frac{4}{12}-\frac{3}{12}=\frac{9}{12}=\frac{3}{4}. Thus, the correct answer is \frac{3}{4}.
The average score on this problem was 73%.
Suppose we randomly select two of Birgit’s Olympic medals, without replacement. What is the probability both were earned in 1988? Give your answer as a fully simplified fraction.
Answer: \frac{1}{22}
In this problem, we are sampling 2 medals without replacement. Let A be the event that the first medal is from 1988 and let P(B) be the event that the second medal is from 1988. P(A) is \frac{3}{12} since there are 3 medals from 1988 out of the total 12 medals. However, in the second trial, since we are sampling without replacement, the medal that we just sampled is no longer in our pool. Thus, P(B) is now \frac{2}{11} since there are now 2 medals from 1988 from the remaining 11 total medals. The joint probability P(A \cap B) is P(A)P(B) so, plugging these values in, we get \frac{3}{12} \cdot \frac{2}{11} = \frac{3}{66} = \frac{1}{22}. Thus, the answer is \frac{1}{22}.
The average score on this problem was 57%.
Recall that the game Clue comes with 22 cards, one for each of the 6 suspects, 7 weapons, and 9 rooms. One suspect card, one weapon card, and one room card are chosen randomly, without being looked at, and placed aside in an envelope. The remaining 19 cards (5 suspects, 6 weapons, 8 rooms) are randomly shuffled and dealt out, splitting them as evenly as possible among the players. Suppose in a three-player game, Janine gets 6 cards, which are dealt one at a time.
Answer the probability questions that follow. Leave your answers unsimplified.
Cards are dealt one at a time. What is the probability that the first card Janine is dealt is a weapon card?
Answer: \frac{6}{19}
The probability of getting a weapon card is just the number of weapon cards divided by the total number of cards. There are 6 weapon cards and 19 cards total, so the probability has to be \frac{6}{19}. Note that it does not matter how the cards were dealt. Though each card is dealt one at a time to each player, Janine will always end up with a randomly selected 6 cards, out of the 19 cards available.
The average score on this problem was 80%.
What is the probability that all 6 of Janine’s cards are weapon cards?
Answer: \frac{6}{19} \cdot \frac{5}{18} \cdot \frac{4}{17} \cdot \frac{3}{16} \cdot \frac{2}{15} \cdot \frac{1}{14}
We can calculate the answer using the multiplication rule. The probability of getting Janine getting all the weapon cards is the probability of getting a dealt a weapon card first multiplied by the probability of getting a weapon card second multiplied by continuing probabilities of getting a weapon card until probability of getting a weapon card on the sixth draw. The denominator of each subsequent probability decreases by 1 because we remove one card from the total number of cards on each draw. The numerator also decreases by 1 because we remove a weapon card from the total number of available weapon cards on each draw.
The average score on this problem was 62%.
Determine the probability that exactly one of the first two cards Janine is dealt is a weapon card. This probability can be expressed in the form \frac{k \cdot (k + 1)}{m \cdot (m + 1)} where k and m are integers. What are the values of k and m?
Hint: There is no need for any sort of calculation that you can’t do easily in your head, such as long division or multiplication.
Answer: k = 12, m = 18
m has to be 18 because the denominator is the number of cards available during the first and second draw. We have 19 cards on the first draw and 18 on the second draw, so the only way to get that is for m = 18.
The probability that exactly one of the cards of your first two draws is a weapon card can be broken down into two cases: getting a weapon card first and then a non-weapon card, or getting a non-weapon card first and then a weapon card. We add the probabilities of the two cases together in order to calculate the overall probability, since the cases are mutually exclusive, meaning they cannot both happen at the same time.
Consider first the probability of getting a weapon card followed by a non-weapon card. This probability is \frac{6}{19} \cdot \frac{13}{18}. Similarly, the probability of getting a non-weapon card first, then a weapon card, is \frac{13}{19} \cdot \frac{6}{18}. The sum of these is \frac{6 \cdot 13}{19 \cdot 18} + \frac{13 \cdot 6}{19 \cdot 18}.
Since we want the numerator to look like k \cdot (k+1), we want to combine the terms in the numerator. Since the fractions in the sum are the same, we can represent the probability as 2 \cdot \frac{6}{19} \cdot \frac{13}{18}. Since 2\cdot 6 = 12, we can express the numerator as 12 \cdot 13, so k = 12.
The average score on this problem was 31%.
When new students arrive at Hogwarts, they get assigned to one of the four houses (Gryffindor, Hufflepuff, Ravenclaw, Slytherin) by a magical Sorting Hat.
Throughout this problem, we’ll assume that the Sorting Hat assigns students to houses uniformly at random, meaning that each student has an independent 25% chance of winding up in each of the four houses.
For all parts, give your answer as an unsimplified mathematical expression.
There are seven siblings in the Weasley family: Bill, Charlie, Percy, Fred, George, Ron, and Ginny. What is the probability that all seven of them are assigned to Gryffindor?
Answer: \left(0.25\right)^{7}
The probability that a student gets assigned to Gryffindor is 0.25 (or \frac{1}{4}). Since we are given that the Sorting Hat assigns students independently, we can apply the multiplication rule and multiply the probability of each of the seven Weasleys being sorted to Gryffindor together. Therefore, all terms in our product are 0.25. Thus, the probability that all seven Weasleys get assigned to Gryffindor would be 0.25 * 0.25 * \ldots * 0.25 = \left(0.25\right)^{7}.
The average score on this problem was 94%.
What is the probability that Fred and George Weasley are assigned to the same house?
Answer: 0.25
Fred and George are assigned to the same house if both are in Gryffindor, or both are in Hufflepuff, etc.. Fred and George’s selections from the sorting hat are independent. Using the multiplication rule, P(both in Gryffindor) = 0.25 * 0.25. Likewise, P(both in Hufflepuff) = 0.25 * 0.25. It is the same for Ravenclaw and Slytherin as well. Therefore, P(same house) = 4 * (0.25 * 0.25) = 0.25.
The average score on this problem was 68%.
What is the probability that none of the seven Weasley siblings are assigned to Slytherin?
Answer: \left(0.75\right)^{7}
The probability that none of the seven Weasley siblings are assigned to Slytherin is equal to the probability that all of the Weasley siblings are not assigned to Slytherin. The probability that someone is not assigned to Slytherin is 1 - P(Slytherin) = 1 - 0.25 = 0.75. Since we are given that the Sorting Hat assigns students independently, we can apply the multiplication rule and multiply the probability of each of the seven Weasleys being sorted to anywhere but Slytherin together. Therefore, all terms in our product are 0.75. Thus, the probability that none of seven Weasleys get assigned to Slytherin would be 0.75 * 0.75 * \ldots * 0.75 = \left(0.75\right)^{7}.
The average score on this problem was 67%.
Suppose you are told that none of the seven Weasley siblings are assigned to Slytherin. Based on this information, what is the probability that at least one of the siblings is assigned to Gryffindor?
Answer: 1 - \left(\frac{2}{3}\right)^{7}
Since we are given that none of the Weasley siblings are assigned to Slytherin, our possibilities are now only Gryffindor, Hufflepuff, and Ravenclaw. Therefore, the probability that someone is assigned to Gryffindor would become \frac{1}{3}. Correspondingly, the probability that someone isn’t assigned to Gryffindor is 1 - \frac{1}{3} = \frac{2}{3}. The probability that at least one of the siblings is assigned to Gryffindor is equal to 1 - the probability that none of the siblings are assigned to Gryffindor, or 1 - \left(\frac{2}{3}\right)^{7}.
The average score on this problem was 51%.
