Lecture 12 — Practice

Below are practice problems tagged for Lecture 12 (rendered directly from the original exam/quiz sources).

Problem 1

King Triton has boarded a Southwest flight. For in-flight refreshments, Southwest serves four types of cookies – chocolate chip, gingerbread, oatmeal, and peanut butter.

The flight attendant tells King Triton to grab 2 cookies out of the box without looking.

Fill in the blanks below to implement a simulation that estimates the probability that both of King Triton’s selected cookies are the same.

Problem 1.1

Answer: cookie_box, 2, replace=False

We are told that King Triton grabs two cookies out of the box without looking. Since this is a random choice, we use the function np.random.choice to simulate this. The first input to this function is a sequence of values to choose from. We already have an array of values to choose from in the variable cookie_box. Calling np.random.choice(cookie_box) would select one cookie from the cookie box, but we want to select two, so we use an optional second parameter to specify the number of items to randomly select. Finally, we should consider whether we want to select with or without replacement. Since cookie_box contains individual cookies and King Triton is selecting two of them, he cannot choose the same exact cookie twice. This means we should sample without replacement, by specifying replace=False. Note that omitting the replace parameter would use the default option of sampling with replacement.

Difficulty: ⭐️

The average score on this problem was 92%.

Problem 1.2

Answer: grab[0] == grab[1]

The idea of a simulation is to do some random process many times. We can use the results to approximate a probability by counting up the number of times some event occurred, and dividing that by the number of times we did the random process. Here, the random process is selecting two cookies from the cookie box, and we are doing this 10,000 times. The approximate probability will be the number of times in which both cookies are the same divided by 10,000. So we need to count up the number of times that both randomly selected cookies are the same. We do this by having an accumulator variable that starts out at 0 and gets incremented, or increased by 1, every time both cookies are the same. The code has such a variable, called prob_both_same, that is initialized to 0 and gets incremented when some condition is met.

We need to fill in the condition, which is that both randomly selected cookies are the same. We’ve already randomly selected the cookies and stored the results in grab, which is an array of length 2 that comes from the output of a call to np.random.choice. To check if both elements of the grab array are the same, we access the individual elements using brackets with the position number, and compare using the == symbol to check equality. Note that at the end of the for loop, the variable prob_both_same will contain a count of the number of trials out of 10,000 in which both of King Triton’s cookies were the same flavor.

Difficulty: ⭐️⭐️

The average score on this problem was 79%.

Problem 1.3

Answer: prob_both_same / repetitions

After the for loop, prob_both_same contains the number of trials out of 10,000 in which both of King Triton’s cookies were the same flavor. We’d like it to represent the approximate probability of both cookies being the same flavor, so we need to divide the current value by the total number of trials, 10,000. Since this value is stored in the variable repetitions, we can divide prob_both_same by repetitions.

Difficulty: ⭐️

The average score on this problem was 93%.

Problem 2

TritonTrucks is an EV startup run by UCSD alumni. Their signature EV, the TritonTruck, has a subpar battery (the engineers didn’t pay attention in their Chemistry courses).

A new TritonTruck’s battery needs to be replaced after 500 days, unless it fails first, in which case it needs to be replaced immediately. On any given day, the probability that a given TritonTruck’s battery fails is 0.02, independent of all other days.

Fill in the blanks so that average_days_until_replacement is an estimate of the average number of days a new TritonTruck’s battery lasts without needing to be replaced.

Answer:

Blank (a): np.arange(len(daily_conditions))
Blank (b): days = days + 1
Blank (c): [True, False]

At a high-level, here’s how this code block works:

daily_conditions is an array of length 500, in each each element is True with probability 0.98 and False with probability 0.02. Each element of daily_conditions is meant to represent whether or not the given TritonTruck’s battery failed on that day. For instance, if the first four elements of daily_conditions are [True, True, False, True, ...], it means the battery was fine the first two days, but failed on the third day.
The function days_until_replacement takes in daily_conditions and returns the number of days until the battery failed for the first time. In other words, it returns the number of elements before the first False in daily_conditions. In the example above, where the first four elements of daily_conditions are [True, True, False, True, ...], days_until_replacement would return 2, since the battery lasted 2 days until it needed to be replaced. It doesn’t matter what is in daily_conditions after the first False.

With that in mind, let’s fill in the pieces.

Blank (a): We need to loop over all elements in daily_conditions. There are two ways to do this, in theory – by looping over the elements themselves (e.g. for cond in daily_conditions) or their positions (e.g. for i in np.arange(len(daily_conditions))). However, here we must loop over their positions, because the body of days_until_replacement uses daily_conditions[i], which only makes sense if i is the position of an element in daily_conditions. Since daily_conditions has 500 elements, the possible positions are 0, 1, 2, …, 499. Since len(daily_conditions) is 500, both np.arange(len(daily_conditions)) and np.arange(500) yield the same correct result here.
Blank (b): days is the “counter” variable that is being used to keep track of the number of days the battery lasted before failing. If daily_conditions[i] is True, it means that the battery lasted another day without failing, and so 1 needs to be added to days. As such, the correct answer here is days = days + 1 (or days += 1). (If daily_conditions[i] is False, then the battery has failed, and so we return the number of days until the first failure.)
Blank (c): This must be [True, False], as mentioned above. There are other valid answers too, including np.array([True, False]) and [1, 0].

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 56%.

Problem 3

After the family reunion, Family Y gets together with nine other families to play a game. All ten families (which we’ll number 1 through 10) have a composition of "2a3c". Within each family, the three children are labeled "oldest", "middle", or "youngest".

In this game, the numbers 1 through 10, representing the ten families, are placed into a hat. Then, five times, they draw a number from the hat, write it down on a piece of paper, and place it back into the hat. If a family’s number is written down on the paper at least twice, then two of the three children in that family are randomly selected to win a prize. The same child cannot be selected to win a prize twice.

Chiachan is the middle child in Family 4. He writes a simulation, which is partially provided on the next page. Fill in the blanks so that after running the simulation,

Problem 3.1

Answer: replace=True

A family can be selected more than once, as indicated by “placing the number back into the hat” in the problem statement. Therefore we use replace=True to allow for the same family to get picked more than once.

Difficulty: ⭐️⭐️

The average score on this problem was 88%.

Problem 3.2

Answer: np.count_nonzero(fams == 4) >= 2 or equivalent

Notice that inside the body of the if statement, the first line defines a variable children which selects two children from among ages. We are told in the problem statement that if a family’s number is written down on the paper at least twice, then two of the three children in that family are randomly selected to win a prize. Therefore, the condition that we want to check in the if statement should correspond to Chiachan’s family number (4) being written down on the paper at least twice.

When we compare the entire fams array to the value 4 using fams == 4, the result is an array of True or False values, where each True represents an instance of Chiachan’s family being chosen. Then np.count_nonzero(fams == 4) evaluates to the number of Trues, because in Python, True is 1 and False is 0. That is, np.count_nonzero(fams == 4) represents the number of times Chichan’s family is selected, and so our condition is np.count_nonzero(fams == 4) >= 2.

There are many equivalent ways to write this same condition, including np.count_nonzero(fams == 4) > 1 and (fams == 4).sum() >= 2.

Difficulty: ⭐️⭐️⭐️⭐️⭐️

The average score on this problem was 17%.

Problem 3.3

Answer: replace=False

A child cannot win a prize twice, so we remove them from the pool after being selected.

Difficulty: ⭐️⭐️

The average score on this problem was 86%.

Problem 3.4

Answer: "Outcome R"

Chiachan is the middle child in the family, and recall that each outcome corresponds to either Chiachan winning ("Outcome Q"), Chiachan not winning but his siblings winning ("Outcome R"), or nobody in his family winning ("Outcome S").

This condition checks the negation of the middle child being selected, which evaluates to True when Chiachan’s siblings win but he doesn’t, so we append "Outcome R" to the outcomes array in this case.

Difficulty: ⭐️⭐️

The average score on this problem was 76%.

Problem 3.5

Answer: "Outcome Q"

This condition corresponds to the middle child being selected, so we append "Outcome Q" to the outcomes array in this case.

Difficulty: ⭐️⭐️

The average score on this problem was 75%.

Problem 3.6

Answer: "Outcome S"

This condition is that Chichan’s family was not selected two or more times, which means nobody in his family will win a prize, so we append "Outcome S" to the outcomes array in this case.

Difficulty: ⭐️⭐️

The average score on this problem was 80%.

Problem 4

Problem 4.1

Answer: Series

.str.contains works in a series and returns a series of booleans. Each entry is True if it contains a certain string or False otherwise. So the answer is street has the Series data type.

Difficulty: ⭐️⭐️

The average score on this problem was 75%.

Problem 4.2

What does the following expression evaluate to? Write your answer exactly how the output would appear in Python.

Answer: False

np.count_nonzero(street & sour) counts the number of rows that contains the word “Street” in the address column AND also contains the word “Sour” in candy. sour.sum() sums up all the trues and falses, effectively making it a count of rows that contain the word “Sour” in candy. Even if we don’t know the full dataframe, we should be able to figure out that the number of rows that satisfy the condition of both Street AND Sour should be lower than or equal to the number of rows that satisfy Sour by itself. Therefore, it’s impossible for np.count_nonzero(street & sour) > sour.sum() to be True so the answer is False.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 59%.

Problem 5

Suppose you visit another house and their candy bowl is composed of 2 Twix, 3 Rolos, 1 Snickers, 3 M&Ms, and 1 KitKat. You do the same as before and take 3 candies from the bowl at random.

Fill in the blanks in the code below so that prob_all_same evaluates to an estimate of the probability that you get three of the same type of candy.

Problem 5.1

Answer: candy_bowl, 3, replace=False

The question asks us to “take 3 candies from the bowl at random.” In this part, we need to sample 3 candies at random using np.random.choice. Now, we evaluate each option one by one as follows:

candy_bowl, len(candy_bowl), replace=False: The code tries to sample all candies without replacement. However, we are asked to only sample three candies, not all.
candy_bowl, 3, replace=False: The code samples three candies without replacement, which matches the description. This option is correct.
candy_bowl, 3, replace=True: The code samples three candies from the bowl with replacement. Under this setting, the same candy can be selected multiple times in a single grab, which is not realistic.
candy_bowl, repetitions, replace=True: This option attempts to sample repetitions (10,000) candies in a single grab. We are asked to sample three candies per iteration of the loop, not thousands.

Difficulty: ⭐️⭐️

The average score on this problem was 88%.

Problem 5.2

Answer: grab[0] == grab[1] and grab[0] == grab[2]

Here, we need condition that checks if all three candies selected in the grab are the same. We now analyze each option as follows:

grab[0] == "Rolo" and grab[1] == "Rolo" and grab[2] == "Rolo": This condition explicitly checks if all three candies are “Rolo”. While it ensures that the three candies are the same, it only works for “Rolo” and not for other types of candy in the bowl (e.g., “Twix,” “M&M”).
grab[0] == grab[1] and grab[0] == grab[2]: This condition checks if the first candy (grab[0]) is the same as the second (grab[1]) and the third (grab[2]). If all three candies are the same type (regardless of which type), this condition will evaluate to True. Otherwise, the expression will evaluate to False, which is what we need. The option is correct.
grab[0] == grab[1] or grab[0] == grab[2]: This condition checks if the first candy (grab[0]) matches either the second (grab[1]) or the third (grab[2]). It does not require all three candies to be the same. For example, if grab = [“Twix”, “Twix”, “M&M”], this condition would incorrectly evaluate to True.
grab == "Rolo" | grab == "M&M": This condition is syntactically invalid. It tries to compare the grab list (which contains three elements) with two strings (“Rolo” and “M&M”) using a bitwise OR (|), not to mention that it does not check if three candies are the same.

Difficulty: ⭐️

The average score on this problem was 92%.

Problem 5.3

Answer: prob_all_same / repetitions

To calculate the estimated probability of drawing three candies of the same type, we divide the total number of successes (prob_all_same, which counts the instances where all three candies are identical) by the total number of iterations (repetitions).

The option prob_all_same.mean() is incorrect because prob_all_same is an integer that accumulates the count of successful trials, not an array or list that supports the .mean() method. Similarly, dividing by len(candy_bowl) or 3 is incorrect, as neither represents the total number of iterations. Therefore, using these values as the denominator would not provide an accurate probability estimate.

Difficulty: ⭐️⭐️

The average score on this problem was 86%.

Problem 6

The fine print of the Sun God festival website says “Ticket does not guarantee entry. Venue subject to capacity restrictions.” RIMAC field, where the 2022 festival will be held, has a capacity of 20,000 people. Let’s say that UCSD distributes 21,000 tickets to Sun God 2022 because prior data shows that 5% of tickets distributed are never actually redeemed. Let’s suppose that each person with a ticket this year has a 5% chance of not attending (independently of all others). What is the probability that at least one student who has a ticket cannot get in due to the capacity restriction? Fill in the blanks in the code below so that prob_angry_student evaluates to an approximation of this probability.

Problem 6.1

Answer: attending.sum() > 20000

Let’s look at the variable attending. Since we’re choosing 21,000 elements from the list [True, False] and there are 21,000 tickets distributed, this code is randomly determining whether each ticket holder will actually attend the festival. There’s a 95% chance of each ticket holder attending, which is reflected in the p=[0.95, 0.05] argument. Remember that np.random.choice returns an array of random choices, which in this case means it will contain 21,000 elements, each of which is True or False.

We want to figure out the probability of at least one ticket holder showing up and not being admitted. Another way to say this is we want to find the probability that more than 20,000 ticket holders show up to attend the festival. The way we approximate a probability through simulation is we repeat a process many times and see how often some event occured. The event we’re interested in this case is that more than 20,000 ticket holders came to Sun God. Since we have an array of True and False values corresponding to whether each ticket holder actually came, we just need to determine if there are more than 20,000 True values in the attending array.

There are several ways to count the number of True values in a Boolean array. One way is to sum the array since in Python True counts as 1 and False counts as 0. Therefore, attending.sum() > 20000 is the condition we need to check here.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 67%.

Problem 6.2

Answer: num_angry = num_angry + 1

Remember our goal in simulation is to repeat a process many times to see how often some event occurs. The repetition comes from the for loop which runs 10,000 times. Each time, we are simulating the process of 21,000 students each randomly deciding whether to show up to Sun God or not. We want to know, out of these 10,000 trials, how frequently more than 20,000 of the students will show up. So when this happens, we want to record that it happened. The standard way to do that is to keep a counter variable that starts at 0 and gets incremented, or increased by one, each time we had more than 20,000 attendees in our simulation.

The framework to do this is already set up because a variable called num_angry is initialized to 0 before the for loop. This variable is our counter variable, meant to count the number of trials, out of 10,000, that resulted in at least one student being angry because they showed up to Sun God with a ticket and were denied entrance. So all we need to do when there are more than 20,000 True values in the attending array is increment this counter by one via the code num_angry = num_angry + 1, sometimes abbreviated as num_angry += 1.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 59%.

Problem 6.3

Answer: num_angry/10000

To calculate the approximate probability, all we need to do is divide the number of trials in which a student was angry by the total number of trials, which is 10,000.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 68%.

Problem 7

Suhani’s passport is currently being renewed, and so she can’t join those on international summer vacations. However, her last final exam is today, and so she decides to road trip through California this week while everyone else takes their finals.

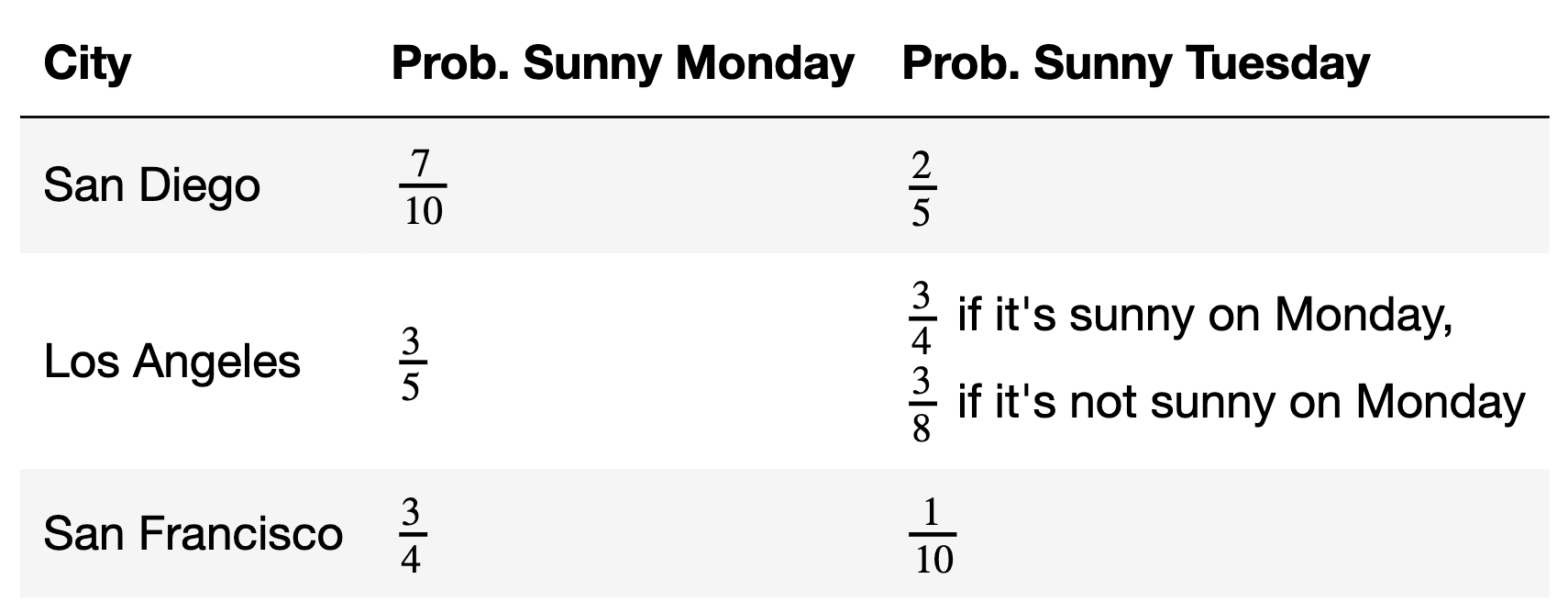
The chances that it is sunny this Monday and Tuesday, in various cities in California, are given below. The event that it is sunny on Tuesday in Los Angeles depends on the event that it is sunny on Monday in Los Angeles, but other than that, all other events in the table are independent of one another.

Problem 7.1

What is the probability that it is not sunny in San Diego on Monday and not sunny in San Diego on Tuesday? Give your answer as a positive integer percentage between 0% and 100%.

Answer: 18%

The probability it is not sunny in San Diego on Monday is 1 - \frac{7}{10} = \frac{3}{10}.
The probability it is not sunny in San Diego on Tuesday is 1 - \frac{2}{5} = \frac{3}{5}.

Since we’re told these events are independent, the probability of both occurring is

\frac{3}{10} \cdot \frac{3}{5} = \frac{9}{50} = \frac{18}{100} = 18\%

Difficulty: ⭐️⭐️

The average score on this problem was 80%.

Problem 7.2

What is the probability that it is sunny in at least one of the three cities on Monday?

Answer: 97\%

The event that it is sunny in at least one of the three cities on Monday is the complement of the event that it is not sunny in all three cities on Monday. The probability it is not sunny in all three cities on Monday is

\big(1 - \frac{7}{10}\big) \cdot \big(1 - \frac{3}{5}\big) \cdot \big(1 - \frac{3}{4}\big) = \frac{3}{10} \cdot \frac{2}{5} \cdot \frac{1}{4} = \frac{6}{200} = \frac{3}{100} = 0.03

So, the probability that it is sunny in at least one of the three cities on Monday is 1 - 0.03 = 0.97 = 97\%.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 65%.

Problem 7.3

Answer: 60\%

The event that it is sunny in Los Angeles on Tuesday can happen in two ways:

Case 1: It is sunny in Los Angeles on Tuesday and on Monday.
Case 2: It is sunny in Los Angeles on Tuesday but not on Monday.

We need to consider these cases separately given the conditions in the table. The probability of the first case is \begin{align*} P(\text{sunny Monday and sunny Tuesday}) &= P(\text{sunny Monday}) \cdot P(\text{sunny Tuesday given sunny Monday}) \\ &= \frac{3}{5} \cdot \frac{3}{4} \\ &= \frac{9}{20} \end{align*}

The probability of the second case is \begin{align*} P(\text{not sunny Monday and sunny Tuesday}) &= P(\text{not sunny Monday}) \cdot P(\text{sunny Tuesday given not sunny Monday}) \\ &= \frac{2}{5} \cdot \frac{3}{8} \\ &= \frac{3}{20} \end{align*}

Since Case 1 and Case 2 are mutually exclusive — that is, they can’t both occur at the same time — the probability of either one occurring is \frac{9}{20} + \frac{3}{20} = \frac{12}{20} = 60\%.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 64%.

Problem 7.4

Fill in the blanks so that exactly_two evaluates to the probability that exactly two of San Diego, Los Angeles, and San Francisco are sunny on Monday.

Hint: If arr is an array, then np.prod(arr) is the product of the elements in arr.

Answer: (a): 0, (b): (1 - monday[i]) / monday[i]

What goes in blank (a)? 0

In the for-loop we add the probabilities of the three different cases, so exactly_two needs to start from 0.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 47%.

What goes in blank (b)? (1 - monday[i]) / monday[i]

In the context of this problem, where we want to find the probability that exactly two out of the three cities (San Diego, Los Angeles, and San Francisco) are sunny on Monday, we need to consider each possible combination where two cities are sunny and one is not. This is done by multiplying the probabilities of two cities being sunny with the probability of the third city not having sunshine and adding up all of the results.

In the code above, np.prod(monday) calculates the probability of all three cities (San Diego, Los Angeles, and San Francisco) being sunny. However, since we’re interested in the case where exactly two cities are sunny, we need to adjust this calculation to account for one of the three cities not being sunny in turn. This adjustment is achieved by the term (1-monday[i]) / monday[i]. Let’s break down this small piece of code together:

1 - monday[i]: This part calculates the probability of the ith city not being sunny. For each iteration of the loop, it represents the chance that one specific city (either San Diego, Los Angeles, or San Francisco, depending on the iteration) is not sunny. This is essential because, for exactly two cities to be sunny, one city must not be sunny.
monday[i]: This part represents the original probability of the ith city being sunny, which is included in the np.prod(monday) calculation.
(1-monday[i]) / monday[i]: By dividing the probability of the city not being sunny by the probability of it being sunny, we’re effectively replacing the ith city’s sunny probability in the original product np.prod(monday) with its not sunny probability. This adjusts the total probability to reflect the scenario where the other two cities are sunny, and the ith city is not.

By adding all possible combinations, it provide the probability that exactly two out of San Diego, Los Angeles, and San Francisco are sunny on a given Monday.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 36%.

Problem 8

We’d like to select three students at random from the entire class to win extra credit (not really). When doing so, we want to guarantee that the same student cannot be selected twice, since it wouldn’t really be fair to give a student double extra credit.

Fill in the blanks below so that prob_all_unique is an estimate of the probability that all three students selected are in different majors.

Hint: The function np.unique, when called on an array, returns an array with just one copy of each unique element in the input. For example, if vals contains the values 1, 2, 2, 3, 3, 4, np.unique(vals) contains the values 1, 2, 3, 4.

Problem 8.1

Answer: replace=False

Since we want to guarantee that the same student cannot be selected twice, we should sample without replacement.

Difficulty: ⭐️⭐️

The average score on this problem was 77%.

Problem 8.2

Aswer: unique_majors

unique_majors is the array we initialized before running our for-loop to keep track of our results. We’re already given that the first argument to np.append is unique_majors, meaning that in each iteration of the for-loop we’re creating a new array by adding a new element to the end of unique_majors; to save this new array, we need to re-assign it to unique_majors.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 65%.

Problem 8.3

Answer: np.unique(group)

In each iteration of our for-loop, we’re interested in finding the number of unique majors among the 3 students who were selected. We can tell that this is what we’re meant to store in unique_majors by looking at the options in the next subpart, which involve checking the proportion of times that the values in unique_majors is 3.

The majors of the 3 randomly selected students are stored in group, and np.unique(group) is an array with the unique values in group. Then, len(np.unique(group)) is the number of unique majors in the group of 3 students selected.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 45%.

Problem 8.4

What could go in blank (d)? Select all that apply. At least one option is correct; blank answers will receive no credit.

Answer: Option 1 only

Let’s break down the code we have so far:

An empty array named unique_majors is initialized to store the number of unique majors in each iteration of the simulation.
The simulation runs 10,000 times, and in every iteration: Three majors are selected at random from the survey dataset without replacement. This ensures that the same item is not chosen more than once within a single iteration. The np.unique function is employed to identify the number of unique majors among the selected three. The result is then appended to the unique_majors array.
Following the simulation, the objective is to determine the fraction of iterations in which all three selected majors were unique. Since the maximum number of unique majors that can be selected in a group of three is 3, the code checks the fraction of times the unique_majors array contains a value greater than 2.

Let’s look at each option more carefully.

Option 1: (unique_majors > 2).mean() will create a Boolean array where each value in unique_majors is checked if it’s greater than 2. In other words, it’ll return True for each 3 and False otherwise. Taking the mean of this Boolean array will give the proportion of True values, which corresponds to the probability that all 3 students selected are in different majors.
Option 2: (unique_majors.sum() > 2) will generate a single Boolean value (either True or False) since you’re summing up all values in the unique_majors array and then checking if the sum is greater than 2. This is not what you want. .mean() on a single Boolean value will raise an error because you can’t compute the mean of a single Boolean.
Option 3: np.count_nonzero(unique_majors > 2).sum() / len(unique_majors > 2) would work without the .sum(). unique_majors > 2 results in a Boolean array where each value is True if the respective simulation yielded 3 unique majors and False otherwise. np.count_nonzero() counts the number of True values in the array, which corresponds to the number of simulations where all 3 students had unique majors. This returns a single integer value representing the count. The .sum() method is meant for collections (like arrays or lists) to sum their elements. Since np.count_nonzero returns a single integer, calling .sum() on it will result in an AttributeError because individual numbers do not have a sum method. len(unique_majors > 2) calculates the length of the Boolean array, which is equal to 10,000 (the total number of simulations). Because of the attempt to call .sum() on an integer value, the code will raise an error and won’t produce the desired result.
Option 4: np.count_nonzero(unique_majors != 3) counts the number of trials where not all 3 students had different majors. When you call .mean() on an integer value, which is what np.count_nonzero returns, it’s going to raise an error.
Option 5: unique_majors.mean() - 3 == 0 is trying to check if the mean of unique_majors is 3. This line of code will return True or False, and this isn’t the right approach for calculating the estimated probability.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 56%.

Problem 9

Arya’s phone number has an interesting property: after the area code (the first three digits), the remaining seven numbers of his phone number consist of only two distinct digits.

Recall from the previous question that when the monkey dials a phone number, each digit it selects is equally likely to be any of the digits 0 through 9. Further, when the cat is dialing a phone number, it makes sure to only use each digit once.

You’re interested in estimating the probability that a phone number dialed by the monkey or the cat has exactly two distinct digits after the area code, like Arya’s phone number. You write the following code, which you plan to use for both the monkey and cat scenarios.

Problem 9.1

First, you want to estimate the probability that the monkey randomly generates a number with only 2 distinct digits after the area code. What code should be used to fill in blank (x)?

Answer: np.random.choice(digits, 7, replace = True) or np.random.choice(digits, 7)

The code simulates the monkey dialing seven digits where each digit is selected randomly from the digits 0 through 9, and digits can repeat (replace = True).

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 50%.

Problem 9.2

Next, you want to estimate the probability that the cat randomly generates a number with only 2 distinct digits after the area code. What code should be used to fill in blank (x)?

Answer: np.random.choice(digits, 7, replace = False)

The code simulates random dialing by a cat without replacement (replace = False). Each digit from 0 to 9 is used only once.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 52%.

Problem 9.3

In either case, whether you’re simulating the monkey or the cat, what should be used to fill in blank (y)?

Answer: num_distinct == 2

This part of the code checks if the number of unique digits in the dialed number is exactly two.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 52%.

Problem 9.4

When you are simulating the cat, what will the value of probability_estimate be after the code executes?

Answer: 0

Since the cat dials each digit without replacement, it’s impossible for the dialed number to contain only two distinct digits (as it would need to repeat some digits to achieve this). Thus, no trial will meet the condition num_distinct == 2, resulting in a property_count of 0 and therefore a probability_estimate of 0.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 53%.

Problem 10

The announcement of the tariffs affected many products, one of which was the Nintendo Switch 2, a new video game console. Due to the tariffs, preorders of the Nintendo Switch 2 were put on hold so pricing could be reconsidered. In this problem, we’ll imagine a scenario in which Nintendo used this delay period to drum up excitement for their new product.

Suppose Nintendo arranges a contest to give away k of their new Switch 2 consoles. The contest is open to anyone and n people participate, with n > k. Everyone has an equal chance of winning, and nobody can win more than once. Jason and Ray both enter the contest, and they want to estimate the probability that they both win.

Problem 10.1

Fill in the blanks in the function giveaway so that it returns an estimate of the probability that Jason and Ray both win a Switch 2, when there are n participants and k prizes.

Answer (a): np.arange(n), k, replace=False

This makes sure that exactly k winners are chosen randomly from n participants without replacement, since no person can win more than once.

Answer (b): 0 in winners and 1 in winners (can be any two numbers)

Assuming Jason and Ray are represented by IDs 0 and 1, this checks whether both of them are in the list of winners for that trial. However, because we never specify what number Jason and Ray are, you could use any two numbers (ie: 1 in winners and 2 in winners)

Answer (c): count/10000

This computes the estimated probability as the fraction of trials where both Jason and Ray won out of 10,000 simulations.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 32%.

Problem 10.2

If you implement giveaway correctly, what should giveaway(100, 100) evaluate to?

Answer: 1.0

Since k is equal to n, everyone wins by default, meaning Jason and Ray will always be among the winners.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 55%.

Problem 10.3

Which of the following could be used to fill in blank (c)? Select all that apply.

Answer: len(results)/10000 and (results == "WIN!").mean()

len(results)/10000 calculates the proportion of trials that resulted in “WIN!”, which gives the probability.
(results == "WIN!").mean() works too because (results == "WIN!") gives a boolean array of True/False, and .mean() calculates the proportion of True values, which again gives the estimated probability.
(results == "WIN!").sum(): This counts the number of “WIN!” results but does not divide by 10000, so it gives a raw count, not a probability.
np.count_nonzero(results): This counts all non empty entries, but since results contains only “WIN!” strings, this is just len(results) and is equivalent to the raw count of wins, not the probability.
np.random.choice(results): This randomly picks an element from results. It is unrelated to calculating a probability and makes no sense in this context.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 55%.

Problem 11

Suppose we run the following code to simulate the winners of the Tour de France.

Problem 11.1

What is the probability that pogacar_wins is equal to 4 when the code finishes running? Do not simplify your answer.

Answer: 0.4 ^ 4

The code runs a loop 4 times, simulating the outcome of each iteration using np.random.multinomial(1, [0.3, 0.3, 0.4]).
The probability that pogacar wins in a single iteration is 0.4 (the third entry in the probability vector [0.3, 0.3, 0.4]).
To win all 4 iterations, pogacar must win independently in each iteration.
Since the trials are independent, the probability is calculated as: 0.4 * 0.4 * 0.4 * 0.4 = 0.4 ^ 4

Difficulty: ⭐️⭐️

The average score on this problem was 88%.

Problem 11.2

What is the probability that evenepoel_wins is at least 1 when the code finishes running? Do not simplify your answer.

Answer: 1 - 0.7 ^ 4

The probability that evenepoel wins in a single iteration is 0.3 (the first entry in the probability vector [0.3, 0.3, 0.4]).
The complement of “at least 1 win” is “no wins at all.” To calculate the complement:
- The probability that evenepoel does not win in a single iteration is: 1 - 0.3 = 0.7
- For evenepoel to win no iterations across all 4 loops, they must fail to win independently in each iteration: 0.7 * 0.7 * 0.7 * 0.7 = 0.7 ^ 4
The probability that evenepoel_wins is at least 1 is then: 1 - 0.7 ^ 4

Difficulty: ⭐️⭐️

The average score on this problem was 83%.

Problem 12

We want to estimate the probability that the University of Michigan is among the four teams selected when schools are selected without replacement.

Problem 12.1

Answer:

1. np.random.choice(schools, 4, replace=False)
1. mystery_one = mystery_one + 1

np.random.choice() allows us to select random samples from the schools array. The correct syntax is np.random.choice(arr, size, replace=True, p=[p_0, p_1, …])

arr: The array to sample from. In this case, schools.
size: The number of elements to draw. In this case, 4, because we want to select four teams.
replace: A boolean value that determines if the same item can be chosen more than once. Since teams cannot be picked more than once in a single selection, we use replace=False.
p: An parameter that sets the probabilities for each item in arr. If omitted, the function assumes each item has an equal chance of being selected. In this problem, we do not need to specify p because we are performing uniform random sampling, meaning every team has an equal chance.

This blank updates mystery_one, which counts how many times “Michigan” appears in the randomly selected teams across the trials. In each iteration of the loop, if “Michigan” is in the randomly selected bracket, we increment mystery_one by 1.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 67%.

Problem 12.2

What is the meaning of mystery_two after the code has finished running? ( ) The number of times Michigan was in the tournament ( ) The number of trials we ran ( ) The proportion of times Michigan was in the tournament ( ) None of these answers is what mystery_two represents

Answer: The proportion of times Michigan was in the tournament

If “Michigan” is found in bracket, mystery_one is incremented by 1. This means mystery_one keeps track of how many times Michigan appears in the four selected teams across all 10,000 trials. Therefore, at the end of the loop, mystery_one contains the total number of trials in which Michigan was selected.

mystery_two is calculated as mystery_one / num_trials. Since mystery_one is the count of trials where Michigan was selected, dividing it by num_trials (the total number of trials) gives the proportion of trials where Michigan was chosen among the four teams.

Difficulty: ⭐️⭐️

The average score on this problem was 81%.

Problem 12.3

For the next two parts only, imagine we wanted to simulate a 16-team tournament, where teams are selected with replacement. Which blank should be filled in?

Answer: blank (i)

When simulating a 16-team tournament, where teams are selected with replacement, Blank (i) should be used because that is where the selection occurs. We need to adjust this line to account for selecting more teams (16 teams) and to allow replacements.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 67%.

Problem 12.4

Answer: np.random.choice(schools, 16, replace=True)

We change size=4 to size=16 to select 16 teams, and replace=True allows the same team to be selected multiple times within a single trial.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 45%.

Problem 13

Billina Records, a new record company focused on creating new TikTok audios, has its offices on the 23rd floor of a skyscraper with 75 floors (numbered 1 through 75). The owners of the building promised that 10 different random floors will be selected to be renovated.

Problem 13.1

Below, fill in the blanks to complete a simulation that will estimate the probability that Billina Records’ floor will be renovated.

Answer: np.arange(1, 76), replace=False, np.count_nonzero(choices == 23) > 0

Here, the idea is to randomly choose 10 different floors repeatedly, and each time, check if floor 23 was selected.

Blank (a): The first argument to np.random.choice needs to be an array/list containing the options we want to choose from, i.e. an array/list containing the values 1, 2, 3, 4, …, 75, since those are the numbers of the floors. np.arange(a, b) returns an array of integers spaced out by 1 starting from a and ending at b-1. As such, the correct call to np.arange is np.arange(1, 76).

Blank (b): Since we want to select 10 different floors, we need to specify replace=False (the default behavior is replace=True).

Blank (c): The if condition needs to check if 23 was one of the 10 numbers that were selected, i.e. if 23 is in choices. It needs to evaluate to a single Boolean value, i.e. True (if 23 was selected) or False (if 23 was not selected). Let’s go through each incorrect option to see why it’s wrong:

Option 1, choices == 23, does not evaluate to a single Boolean value; rather, it evaluates to an array of length 10, containing multiple Trues and Falses.
Option 2, choices is 23, does not evaluate to what we want – it checks to see if the array choices is the same Python object as the number 23, which it is not (and will never be, since an array cannot be a single number).
Option 4, np.count_nonzero(choices) == 23, does evaluate to a single Boolean, however it is not quite correct. np.count_nonzero(choices) will always evaluate to 10, since choices is made up of 10 integers randomly selected from 1, 2, 3, 4, …, 75, none of which are 0. As such, np.count_nonzero(choices) == 23 is the same as 10 == 23, which is always False, regardless of whether or not 23 is in choices.
Option 5, choices.str.contains(23), errors, since choices is not a Series (and .str can only follow a Series). If choices were a Series, this would still error, since the argument to .str.contains must be a string, not an int.

By process of elimination, Option 3, np.count_nonzero(choices == 23) > 0, must be the correct answer. Let’s look at it piece-by-piece:

As we saw in Option 1, choices == 23 is a Boolean array that contains True each time the selected floor was floor 23 and False otherwise. (Since we’re sampling without replacement, floor 23 can only be selected at most once, and so choices == 23 can only contain the value True at most once.)
np.count_nonzero(choices == 23) evaluates to the number of Trues in choices == 23. If it is positive (i.e. 1), it means that floor 23 was selected. If it is 0, it means floor 23 was not selected.
Thus, np.count_nonzero(choices == 23) > 0 evaluates to True if (and only if) floor 23 was selected.

Difficulty: ⭐️⭐️

The average score on this problem was 75%.

Problem 13.2

In the previous subpart of this question, your answer to blank (c) contained the number 23, and the simulated probability was stored in the variable prob_renovate.

Suppose, in blank (c), we change the number 23 to the number 46, and we store the new simulated probability in the variable name other_prob. (prob_renovate is unchanged from the previous part.)

With these changes, which of the following is the most accurate representation of the relationship between other_prob and prob_renovate?

Answer: other_prob will be roughly equal to prob_renovate

The calculation we did in the previous subpart was not specific to the number 23. That is, we could have replaced 23 with any integer between 1 and 75 inclusive and the simulation would have been just as valid. The probability we estimated is the probability that any one floor was randomly selected; there is nothing special about 23.

(We say “roughly equal” because the result may turn out slightly different due to randomness.)

Difficulty: ⭐️⭐️

The average score on this problem was 89%.

Problem 14

Dylan, Harshi, and Selim are playing a variant of a dice game called Left, Center, Right (LCR) in which there are 9 chips (tokens) and 9 dice. Each player starts off with 3 chips. Each die has the following six sides: L, C, R, Dot, Dot, Dot.

During a given player’s turn, they must roll a number of dice equal to the number of chips they currently have. Each die determines what to do with one chip:

Since the number of dice rolled is the same as the number of chips the player has, the dice rolls determine exactly what to do with each chip. There is no strategy at all in this simple game.

Dylan will take his turn first (we’ll call him Player 0), then at the end of his turn, he’ll pass the dice to his left and play will continue clockwise around the table. Harshi (Player 1) will go next, then Selim (Player 2), then back to Dylan, and so on.

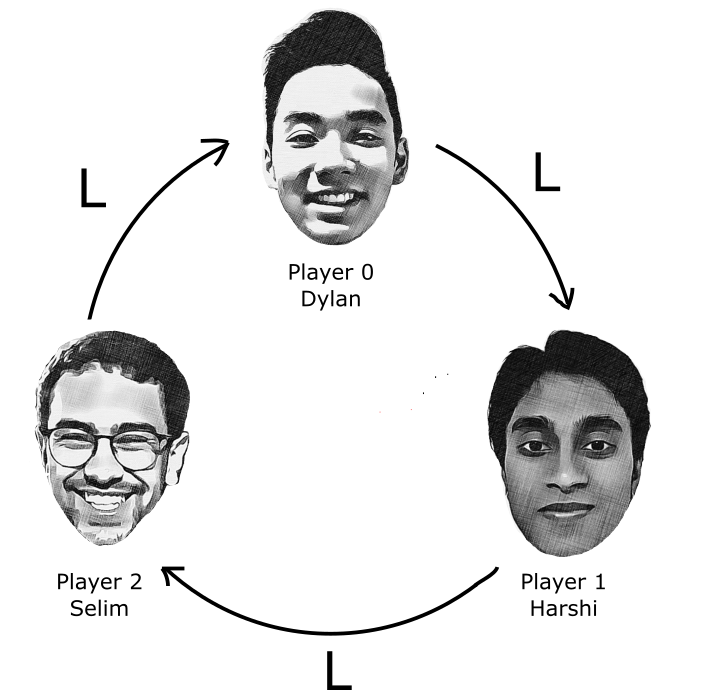
Note that if someone has no chips when it’s their turn, they are still in the game and they still take their turn, they just roll 0 dice because they have 0 chips. The game ends when only one person is holding chips, and that person is the winner. If 300 turns have been taken (100 turns each), the game will end and we’ll declare it a tie.

The function simulate_lcr below simulates one full game of Left, Center, Right and returns the number of turns taken in that game. Some parts of the code are not provided. You will need to fill in the code for the parts marked with a blank. The parts marked with ... are not provided, but you don’t need to fill them in because they are very similar to other parts that you do need to complete.

Hint: Recall that in Python, the % operator gives the remainder upon division. For example 12 % 5 is 2.

Problem 14.1

Answer: i % 3

We are trying to find which player’s turn it is within the for-loop. We know that each player: Dylan, Harshi, and Selim will play a maximum of 100 turns. Notice that the for-loop goes from 0 to 299. This means we need to manipulate the i somehow to figure out whose turn it is. The hint here is extremely helpful. The maximum remainder we want to have is 2 (recall the players are called Player 0, Player 1, and Player 2). This means we can utilize % to give us the remainder of i / 3, which would tell us which player’s turn it is.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 41%.

Problem 14.2

Answer: player_chips[current_player]

Recall np.random.choice() must be given an array and can then optionally be given a size to get multiple values instead of one. We know that player_chips is an array of the chips for each player. To access a specific player’s chips we can use [current_player] because the 1st index of player_chips corresponds to Player 0, the 2nd index corresponds to Player 1, and the 3rd index corresponds to Player 2.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 51%.

Problem 14.3

Answer: `np.count_nonzero(roll == “L”)

We know that if we do roll == “L” then we get an array which changes the index of each element in roll to True if that element equals “L” and False otherwise. We can then use np.count_nonzero() to count the number of True values there are.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 61%.

Problem 14.4

Answer: [-(L_count + C_count + R_count), L_count, R_count]

Recall the rules of the games:

L means give the chip to the player on their left.
R means give the chip to the player on their right.
C means put the chip in the center of the table. This chip is now out of play.
Dot means do nothing (or keep the chip)

If we are Player 0 the person to our left is Player 1 and the person to our right is Player 2. We want to update player_chips to appropriately give the players to our left and right chips. This means we can add our own array with the element at index 1 be our L_count and the element at index 2 be our R_count. We need to also subtract the tokens we are giving away and C_count, so in index 0 we have: -(L_count + C_count + R_count).

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 51%.

Problem 14.5

Answer: np.count_nonzero(player_chips) == 1

We want to stop the game early if only one person has chips. To do this we can use np.count_nonzero(player_chips) to count the number of elements inside player_chips that have chips. If the player does not have chips then their index would have 0 inside of it.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 61%.

Problem 14.6

Answer: i + 1

To find the number of turns played we simply need to add 1 to i. We do this because i starts at 0!

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 53%.

Problem 15

Which of the following probabilities could most easily be approximated by writing a simulation in Python? Select the best answer.

Answer: The probability that Janine has three or more suspect cards.

Let’s explain each choice and why it would be easy or difficult to simulate in Python. The first choice is difficult because these simulations depend on Janine’s strategies and decisions in the game. There is no way to simulate people’s choices. We can only simulate randomness. For the second choice, we are not given information on how long each part of the gameplay takes, so we would not be able to simulate the length of a game. The third choice is very plausible to do because when cards are dealt out to Janine, this is a random process which we can simulate in code, where we keep track of whether she has three of more suspect cards. The fourth choice follows the same reasoning as the first choice. There is no way to simulate Janine’s moves in the game, as it depends on the decisions she makes while playing.

Difficulty: ⭐️⭐️

The average score on this problem was 83%.

Problem 16

Among Hogwarts students, Chocolate Frogs are a popular enchanted treat. Chocolate Frogs are individually packaged, and every Chocolate Frog comes with a collectible card of a famous wizard (ex.”Albus Dumbledore"). There are 80 unique cards, and each package contains one card selected uniformly at random from these 80.

Neville would love to get a complete collection with all 80 cards, and he wants to know how many Chocolate Frogs he should expect to buy to make this happen.

Suppose we have access to a function called frog_experiment that takes no inputs and simulates the act of buying Chocolate Frogs until a complete collection of cards is obtained. The function returns the number of Chocolate Frogs that were purchased. Fill in the blanks below to run 10,000 simulations and set avg_frog_count to the average number of Chocolate Frogs purchased across these experiments.

Problem 16.1

Answer: frog_counts, frog_experiment()

Each call to frog_experiment() simulates purchasing Chocolate Frogs until a complete set of 80 unique cards is obtained, returning the total number of frogs purchased in that simulation. The result of each simulation is then appended to the frog_counts array.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 65%.

Problem 16.2

Answer: frog_counts.mean()

After running the loop for 10000 times, the frog_counts array holds all the simulated totals. Taking the mean of that array (frog_counts.mean()) gives the average number of frogs needed to complete the set of 80 unique cards.

Difficulty: ⭐️⭐️

The average score on this problem was 89%.

Problem 16.3

Realistically, Neville can only afford to buy 300 Chocolate Frog cards. Using the simulated data in frog_counts, write a Python expression that evaluates to an approximation of the probability that Neville will be able to complete his collection.

Answer: np.count_nonzero(frog_counts <= 300) / len(frog_counts) or equivlent, such as np.count_nonzero(frog_counts <= 300) / 10000 or (frog_counts <= 300).mean()

In the simulated data, each entry of frog_counts is the number of Chocolate Frogs purchased in one simulation before collecting all 80 unique cards. We want to estimate the probability that Neville completes his collection with at most 300 cards.

frog_counts <= 300 creates a boolean array of the same length as frog_counts, where each element is True if the number of frogs used in that simulation was 300 or fewer, and False otherwise.

np.count_nonzero(frog_counts <= 300) counts how many simulations (out of all the simulations) met the condition since True evaluates to 1 and False evaluates to 0.

Dividing by the total number of simulations, len(frog_counts), converts that count to probability.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 59%.

Problem 16.4

True or False: The Central Limit Theorem states that the data in frog_counts is roughly normally distributed.

Answer: False

The Central Limit Theorem (CLT) says that the probability distribution of the sum or mean of a large random sample drawn with replacement will be roughly normal, regardless of the distribution of the population from which the sample is drawn.

The Central Limit Theorem (CLT) does not claim that individual observations are normally distributed. In this problem, each entry of frog_counts is a single observation: the number of frogs purchased in one simulation to complete the collection. There is no requirement that these individual data points themselves follow a normal distribution.

However, if we repeatedly take many samples of such observations and compute the sample mean, then that mean would tend toward a normal distribution as the sample size grows, follows the CLT.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 38%.

Problem 17

It’s the grand opening of UCSD’s newest dining attraction: The Bread Basket! As a hardcore bread enthusiast, you celebrate by eating as much bread as possible. There are only a few menu items at The Bread Basket, shown with their costs in the table below:

Bread	Cost
Sourdough	2
Whole Wheat	3
Multigrain	4

Suppose you are given an array eaten containing the names of each type of bread you ate.

In this example, eaten represents five slices of bread that you ate, for a total cost of \$12. Pricey!

In this problem, you’ll calculate the total cost of your bread-eating extravaganza in various ways. In all cases, your code must calculate the total cost for an arbitrary eaten array, which might not be exactly the same as the example shown above.

Problem 17.1

One way to calculate the total cost of the bread in the eaten array is outlined below. Fill in the missing code.

Answer (a): [0, 1, 2] or np.arange(len(bread)) or range(3) or equivalent

Let’s read through the code skeleton and develop the answers from intuition. First, we notice a for loop, but we don’t yet know what sequence we’ll be looping through.

Then we notice a variable total_cost that is initalized to 0. This suggests we’ll use the accumulator pattern to keep a running total.

Inside the loop, we see that we are indeed adding onto the running total. The amount by which we increase total_cost is np.count_nonzero(eaten == __(b)__) * __(c)__. Let’s remember what this does. It first compares the eaten array to some value and then counts how many True values are in resulting Boolean array. In other words, it counts how many times the entries in the eaten array equal some particular value. This is a big clue about how to fill in the code. There are only three possible values in the eaten array, and they are "Sourdough", "Whole Wheat", and "Multigrain". For example, if blank (b) were filled with "Sourdough", we would be counting how many of the slices in the eaten array were "Sourdough". Since each such slice costs 2 dollars, we could find the total cost of all "Sourdough" slices by multiplying this count by 2.

Understanding this helps us understand what the code is doing: it is separately computing the cost of each type of bread ("Sourdough", "Whole Wheat", "Multigrain") and adding this onto the running total. Once we understand what the code is doing, we can figure out how to fill in the blanks.

We just discussed filling in blank (b) with "Sourdough", in which case we would have to fill in blank (c) with 2. But that just gives the contribution of "Sourdough" to the overall cost. We also need the contributions from "Whole Wheat" and "Multigrain". Somehow, blank (b) needs to take on the values in the provided breads array. Similarly, blank (c) needs to take on the values in the prices array, and we need to make sure that we iterate through both of these arrays simultaneously. This means we should access breads[0] when we access prices[0], for example. We can use the loop variable i to help us, and fill in blank (b) with breads[i] and blank (c) with prices[i]. This means i needs to take on the values 0, 1, 2, so we can loop through the sequence [0, 1, 2] in blank (a). This is also the same as range(len(bread)) and range(len(price)).

Bravo! We have everything we want, and the code block is now complete.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 58%.

Answer (b): breads[i]

See explanation above.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 61%.

Answer (c): prices[i]

See explanation above.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 61%.

Problem 17.2

Another way to calculate the total cost of the bread in the eaten array uses the merge method. Fill in the missing code below.

Answer (d): "Type"

It always helps to sketch out the DataFrames.

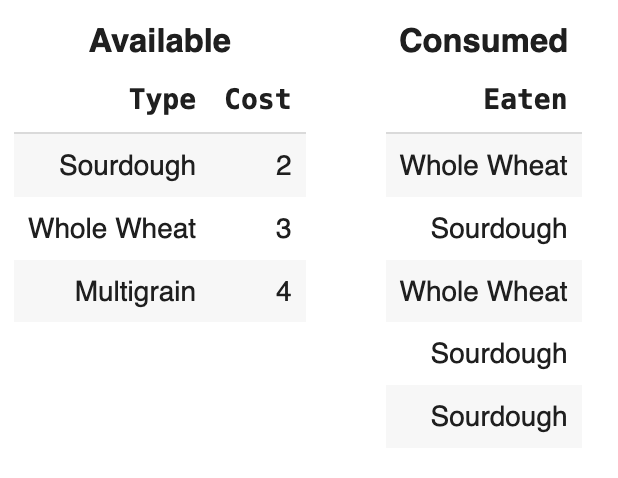
Let’s first develop some intuition based on the keywords.

We create two DataFrames as seen above, and we perform a merge) operation. We want to fill in what columns to merge on. It should be easy to see that blank (e) would be the "Eaten" column in consumed, so let’s fill that in.
We are getting total_cost from the combined DataFrame in some way. If we want the total amount of something, which aggregation function might we use?

In general, if we have df_left.merge(df_right, left_on=col_left, right_on=col_right), assuming all entries are non-empty, the merge process looks at individual entries from the specified column in df_left and grabs all entries from the specified column in df_right that matches the entry content. Based on this, we know that the combined DataFrame will contain a column of all the breads we have eaten and their corresponding prices. Blank (d) is also settled: we can get the list of all breads by merging on the "Type" column in available to match with "Eaten".

Difficulty: ⭐️⭐️

The average score on this problem was 81%.

Answer (e): "Eaten"

See explanation above.

Difficulty: ⭐️⭐️

The average score on this problem was 80%.

Answer (f): get("Cost").sum()

The combined DataFrame would look something like this:

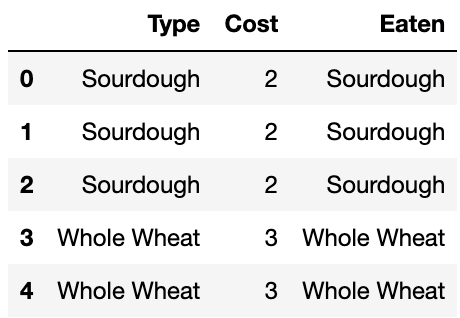
To get the total cost of the bread in "Eaten", we can take the sum of the "Cost" column.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 70%.

Problem 18

At OceanView Terrace, you can make a custom pizza. There are 6 toppings available. Suppose you include each topping with a probability of 0.5, independently of all other toppings.

Problem 18.1

What is the probability you create a pizza with no toppings at all? Give your answer as a fully simplified fraction.

Answer: 1/64

We want the probability that we create a pizza with no toppings at all, which is to say 0 toppings. That means all 6 of the toppings need to be not included on the pizza. In other words, the probability we want is:

P(\text{Not topping 1} \text{ AND Not topping 2} \dots \text{ AND Not topping 6})

The problem statement gives us two important pieces of information that we use to calculate this probability:

The probability of including every topping is independent of every other topping.

The independence of including different toppings means that the probability that we create a pizza with 0 toppings can be framed as a product of probabilities: P(\text{Not topping 1}) \cdot P(\text{Not topping 2}) \cdot ... \cdot P(\text{Not topping 6})
The probability of including a topping is 0.5

This means that the probability of not including each topping is 1 - 0.5 = 0.5.

Therefore, the probability of creating a pizza with no toppings is 0.5 \cdot 0.5 \cdot 0.5 \cdot 0.5 \cdot 0.5 \cdot 0.5 = (0.5)^6 = \frac{1}{64}.

Difficulty: ⭐️⭐️

The average score on this problem was 75%.

Problem 18.2

What is the probability that you create a pizza with exactly three toppings? Fill in the blanks in the code below so that toppa evaluates to an estimate of this probability.

Answer (a): 6

Blank(a) is the size parameter of np.random.choice which determines how many random choices we need to make. To determine what value belongs here, consider the context of the code.

We are defining a variable pizza, representing one simulated pizza. As we are trying to estimate the probability of including exactly three toppings on a pizza, we can simulate the creation of one pizza by deciding whether to include each of the 6 toppings.

Further, we have instructed np.random.choice to select from the list [0, 1]. These are the possible outcomes, which represent whether we include a topping (1) or don’t (0). So, we must randomly choose one of these options 6 times, once per topping.

We are making these choices independently, so each time we choose, we have an equal chance of selecting 0 or 1. This means it’s possible to get several 0s or several 1s, so we are selecting with replacement. Keep in mind that the default behavior of np.random.choice uses replace=True, so we don’t need to specify replace=True anywhere in the code, though it would not be wrong to include it.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 58%.

Answer (b): count_nonzero(pizza) or sum(pizza)

pizza is an array of 0s and 1s, representing whether we include a topping (1) or don’t (0), for each of the 6 toppings. At this step, we want to check if we have three toppings, or if there are exactly three 1’s in our array. We can either do this by counting how many non-zero elements occur, using np.count_nonzero(pizza), or by finding the sum of this array, because the sum is the total number of 1s. Note that the .sum() array method and the built-in function sum() do not fit the structure of the code, which provides us with np. We can, however, use the numpy function np.sum(), which satisfies the constraints of the problem.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 58%.

Answer (c): tiptop + 1

tiptop is a counter representing the number times we had exactly three toppings in our simulation. We want to add 1 to it every time we have exactly three different toppings, or when we satisfy the above condition (np.count_nonzero(pizza) == 3). This is important so that by the end of the simulation, we have a total count of the number of times we had exactly three toppings.

Difficulty: ⭐️⭐️

The average score on this problem was 81%.

Answer (d): tiptop / num_trials

tiptop is the number times we had exactly three toppings in our simulation. To convert this count into a proportion, we need to divide it by the total number of trials in our simluation, or num_trials.

Difficulty: ⭐️⭐️

The average score on this problem was 84%.

Lecture 12 — Collected Practice Questions

Problem 1

Problem 1.1

Click to view the solution.

Difficulty: ⭐️

Problem 1.2

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 1.3

Click to view the solution.

Difficulty: ⭐️

Problem 2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 3

Problem 3.1

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 3.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️⭐️

Problem 3.3

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 3.4

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 3.5

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 3.6

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 4

Problem 4.1

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 4.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 5

Problem 5.1

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 5.2

Click to view the solution.

Difficulty: ⭐️

Problem 5.3

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 6

Problem 6.1

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 6.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 6.3

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 7

Problem 7.1

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 7.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 7.3

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 7.4

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️

Difficulty: ⭐️⭐️⭐️⭐️

Problem 8

Problem 8.1

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 8.2

Click to view the solution.