Spring 2023 Midterm Exam

Recall, at the start of the quarter, you were asked to complete a Welcome Survey to tell us about your background coming into the course. You were also asked to share seemingly irrelevant details, like the number of followers you have on Instagram and the number of unread emails in your primary email account. Well, those details are no longer irrelevant – in this exam, we will work with the data from this quarter’s Welcome Survey!

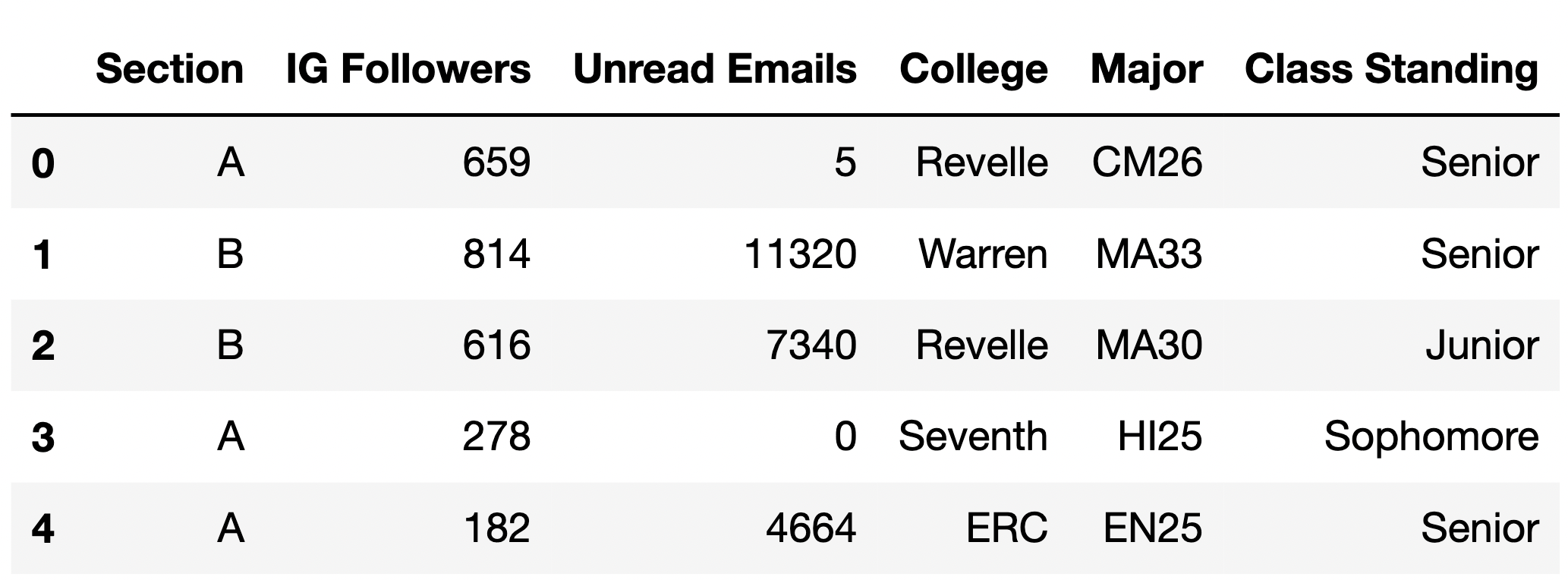
Each row in the DataFrame survey represents one student in DSC 10. The information stored in the columns of survey are as follows:

The first few rows of survey are shown below, though survey has many more rows than are pictured below (since there are more than 5 students in DSC 10 this quarter).

Assume that we have already run import babypandas as bpd and import numpy as np.

Problem 1

Problem 1.1

Answer: DataFrame

The method .sort_values(by="Class Standing") sorts the survey DataFrame by the "Class Standing" column and returns a new DataFrame (without modifying the original one). The resulting DataFrame will be sorted by class standing in ascending order unless specified otherwise by providing the ascending=False argument.

Difficulty: ⭐️

The average score on this problem was 94%.

Problem 1.2

Answer: DataFrame

The method .sort_values(by="Class Standing") sorts the survey DataFrame based on the entries in the "Class Standing" column and produces a new DataFrame. Following this, .groupby("College") organizes the sorted DataFrame by grouping entries using the "College" column. After that, the .count() aggregation method computes the number of rows for each "College". The result is a DataFrame whose index contains the unique values in "College" and whose columns all contain the same values – the number of rows in survey.sort_values(by="Class Standing") for each "College".

Note that if we didn’t sort before grouping – that is, if our expression was just survey.groupby("College").count() – the resulting DataFrame would be the same! That’s because the order of the rows in survey does not impact the number of rows in survey that belong to each "College".

Difficulty: ⭐️

The average score on this problem was 93%.

Problem 1.3

Answer: Series

The above expression, before .get("IG Followers"), is the same as in the previous subpart. We know that

survey.sort_values(by="Class Standing").groupby("College").count()

is a DataFrame indexed by "College" with multiple columns, each of which contain the number of rows in survey.sort_values(by="Class Standing") for each "College". Then, using .get("IG Followers") extracts just the "IG Followers" column from the aforementioned counts DataFrame, and we know that columns are stored as Series. We know that this column exists, because survey.sort_values(by="Class Standing").groupby("College").count() will have the same columns as survey, minus "College", which was moved to the index.

Difficulty: ⭐️

The average score on this problem was 92%.

Problem 1.4

Answer: int or float

In the previous subpart, we saw that

survey.sort_values(by="Class Standing").groupby("College").count().get("IG Followers")

is a Series whose index contains the unique names of "College"s and whose values are the number of rows in survey.sort_values(by="Class Standing") for each college. The number of rows in survey.sort_values(by="Class Standing") for any particular college – say, "Sixth" – is a number, and so the values in this Series are all numbers. As such, the answer is int or float.

Difficulty: ⭐️

The average score on this problem was 91%.

Problem 1.5

What value does the following expression evaluate to? If you believe the expression errors, provide a one sentence explanation of why.

For example, if you think the expression evaluates to an int, don’t write “int" or”the largest value in the "IG Followers" column", write the specific int, like “23".

Hint: You have enough information to answer the problem; don’t forget to look at the data description page.

Answer: "ERC"

From the previous subpart, we saw that

survey
.sort_values(by="Class Standing")
.groupby("College").count()
.get("IG Followers")

is a Series, indexed by "College", whose values contain the number of rows in survey.sort_values(by="Class Standing") for each "College". When we group by "College", the resulting DataFrame (and hence, our Series) is sorted in ascending order by "College". This means that the index of our Series is sorted alphabetically by "College" names. Of the "College" names mentioned in the data description ("ERC", "Marshall", "Muir", "Revelle", "Seventh", "Sixth", and "Warren"), the first name alphabetically is "ERC", so using .index[0] on the above index gives us "ERC".

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 32%.

Problem 1.6

but keep all other parts the same. Does this change the value the expression evaluates to?

Answer: No, this does not change the value the expression evaluates to.

We addressed this in the second subpart of the problem: “Note that if we didn’t sort before grouping – that is, if our expression was just survey.groupby("College").count() – the resulting DataFrame would be the same! That’s because the order of the rows in survey does not impact the number of rows in survey that belong to each "College".”

Difficulty: ⭐️⭐️

The average score on this problem was 80%.

Problem 1.7

What value does the following expression evaluate to? If you believe the expression errors, provide a one sentence explanation of why.

For example, if you think the expression evaluates to an int, don’t write “int” or “the largest value in the "IG Followers" column”, write the specific int, like “23”.

Hint: You have enough information to answer the problem; don’t forget to look at the data description page.

Answer: The code produces an error because, after the grouping operation, the resulting Series uses the unique college names as indices, and there isn’t a college named 0.

In the previous few subparts, we’ve established that

survey
.sort_values(by="Class Standing")
.groupby("College").count()
.get("IG Followers")

is a Series, indexed by "College", whose values contain the number of rows in survey.sort_values(by="Class Standing") for each "College".

The .loc accessor is used to extract a value from a Series given its label, or index value. However, since the index values in the aforementioned Series are "College" names, there is no value whose index is 0, so this throws an error.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 54%.

Problem 2

Fill in the blanks below so that the expression evaluates to the most unread emails of any student that has 0 Instagram followers.

Problem 2.1

Answer: survey.get("IG Followers") == 0

survey.get("IG Followers") is a Series containing the values in the "IG Followers" column. survey.get("IG Followers") == 0, then, is a Series of Trues and Falses, containing True for rows where the number of "IG Followers" is 0 and False for all other rows.

Put together, survey[survey.get("IG Followers") == 0] evaluates to a new DataFrame, which only has the rows in survey where the student’s number of "IG Followers" is 0.

Difficulty: ⭐️⭐️

The average score on this problem was 89%.

Problem 2.2

Answer: Options 2 and 3

Let’s look at each option.

Option 1: get("Unread Emails").apply(max) This option is invalid because .apply(max) will produce a new Series containing the maximums of each individual element in "Unread Emails" rather than the maximum of the entire column. Since the values in the "Unread Emails" columns are numbers, this will try to call max on a number individually (many times), and that errors, since e.g. max(2) is invalid.
Option 2: get("Unread Emails").max() This option is valid because it directly fetches the "Unread Emails" column and uses the max method to retrieve the highest value within it, aligning with the goal of identifying the most unread emails.
Option 3: sort_values("Unread Emails", ascending=False).get("Unread Emails").iloc[0] This option is valid. The sort_values("Unread Emails", ascending=False) method call sorts the "Unread Emails" column in descending order. Following this, .get("Unread Emails") retrieves the sorted column, and .iloc[0] selects the first element, which, given the sorting, represents the maximum number of unread emails.
Option 4: sort_values("Unread Emails", ascending=False).get("Unread Emails").iloc[-1] This option is invalid because, although it sorts the "Unread Emails" column in descending order, it selects the last element with .iloc[-1], which represents the smallest number of unread emails due to the descending sort order.

Difficulty: ⭐️⭐️

The average score on this problem was 89%.

Fill in the blanks below so that revellian is equal to the most unread emails of any student in Revelle, among those with 0 Instagram followers.

Problem 2.3

Answers: (temp.get("College") == "Revelle") & (temp.get("IG Followers") == 0)

To identify the students in "Revelle" with 0 Instagram followers, we filter the temp DataFrame using two conditions: (temp["IG Followers"] == 0) ensures students have no Instagram followers, and (temp["College"] == "Revelle") ensures the student is from "Revelle". The & operator combines these conditions, resulting in a subset of students from "Revelle" with 0 Instagram followers.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 54%.

Problem 2.4

Answer: iloc[0], iloc[-1], sum(), max(), mean(), or any other method that when called on a Series with a single value outputs that same value

To create temp, we grouped on both "IG Followers" and "College" and used the max aggregation method. This means that temp has exactly one row where "College" is "Revelle" and "IG Followers" is 0, since when we group on both "IG Followers" and "College", the resulting DataFrame has exactly one row for every unique combination of "IG Followers" and "College" name. We’ve already identified that before blank (d) is

temp[(temp.get("College") == "Revelle") & (temp.get("IG Followers") == 0)].get("Unread Emails")

Since temp[(temp.get("College") == "Revelle") & (temp.get("IG Followers") == 0)] is a DataFrame with just a single row, the entire expression is a Series with just a single value, being the maximum value we ever saw in the "Unread Emails" column when "College" was "Revelle" and "IG Followers" was 0. To extract the one element out of a Series that only has one element, we can use many aggregation methods (max, min, mean, median) or use .iloc[0] or .iloc[-1].

Difficulty: ⭐️⭐️

The average score on this problem was 79%.

Problem 2.5

The student in Revelle with the most unread emails, among those with 0 Instagram followers, is a "HI25" (History) major. Is the value "HI25" guaranteed to appear at least once within temp.get("Major")?

Answer: No

When the survey DataFrame is grouped by both "IG Followers" and "College" using the .max aggregation method, it retrieves the maximum value for each column based on alphabetical order. Even if a student in "Revelle" with 0 Instagram followers has the most unread emails and is a "HI25" major, the "HI25" value would only be the maximum for the "Major" column if no other major code in the same group alphabetically surpasses it. Therefore, if there’s another major code like "HI26" or "MA30" in that group, it would be chosen as the maximum instead of "HI25".

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 59%.

Problem 3

Currently, the "Section" column of survey contains the values "A" and "B". However, it’s more natural to think of the lecture sections in terms of their times, i.e. "12PM" and "1PM".

Below, we’ve defined four functions, named converter_1, converter_2, converter_3, and converter_4. All four functions return "12PM" when "A" is the argument passed in and return "1PM" when "B" is the argument passed in. Where they potentially differ is in how they behave when called on arguments other than "A" and "B".

Note: In the answer choices below, by None we mean that the function call doesn’t return anything, but doesn’t error either.

Problem 3.1

When convert_1 is called on an argument other than "A" or "B", what does it return?

When convert_2 is called on an argument other than "A" or "B", what does it return?

When converter_3 is called on an argument other than "A" or "B", what does it return?

When converter_4 is called on an argument other than "A" or "B", what does it return?

Answer: converter_1: "1PM", converter_2: It errors, converter_3: It errors, converter_4: None.

converter_1: "1PM". The function converter_1 checks if the input section is equal to "A". If it is, the function returns "12PM". However, if the input is anything other than "A" (including values other than "B"), the function defaults to the else condition and returns "1PM". So, even for arguments other than "A" or "B", converter_1 will return "1PM".

Difficulty: ⭐️

The average score on this problem was 90%.

converter_2: It errors. The function converter_2 utilizes a dictionary (time_dict) to map section values to their corresponding times. When a key that doesn’t exist in the dictionary is accessed (anything other than "A" or "B"), a KeyError is raised, causing the function to error.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 62%.

converter_3: It errors. The function converter_3 specifically checks if the input section is "A" or "B". If the input is neither "A" nor "B", the function defaults to the else condition where it tries to divide 1 by 0. This operation will cause a ZeroDivisionError, leading the function to error.

Difficulty: ⭐️

The average score on this problem was 90%.

converter_4: None. The function converter_4 uses two lists, sections and times, to map the section letters "A" and "B" to their corresponding times "12PM" and "1PM". The function then employs a for-loop to traverse through the sections list. The expression range(len(sections)) is used to generate a sequence of indices for this list; since len(sections) is 2, np.arange(len(sections)) is the array np.array([0, 1]). Then, - Inside the loop, the condition if section == sections[i] checks if the input section matches the section at the current index i of the sections list. If a match is found, the function returns the corresponding time from the times list using return times[i]. - However, if the function traverses the entire sections list without finding a match (i.e., the input is neither "A" nor "B"), no return statement is executed. In Python, if a function completes its execution without encountering a return statement, it implicitly returns the value None. Hence, for inputs other than "A" or "B", converter_4 will return None.

Difficulty: ⭐️⭐️

The average score on this problem was 77%.

Problem 3.2

Suppose we decide to use converter_4 to convert the values in the "Section" column of survey to times. To do so, we first use the .apply method, like so:

We’d then like to replace the "Section" column in survey with the results in section_times. To do so, we run the following line of code, after running the assignment statement above:

Answer:

What is the type of section_times? Series. When the .apply() method is used on a Series in a DataFrame, it applies the given function to each element in the Series and returns a new Series with the transformed values. Thus, the type of section_times is a Series.

Difficulty: ⭐️⭐️

The average score on this problem was 76%.

What is the result of running the above line of code? An error is raised, because the value after the = needs to be a list, array, or Series, not a string. The .assign method is used to add new columns or modify existing columns in a DataFrame. The correct usage would have been to provide the actual Series section_times without quotes. The provided line mistakenly provides a string "section_times" instead of the actual variable, leading to an error.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 52%.

Problem 4

Problem 4.1

Suppose the expression A == B evaluates to True. Given this fact, what can we conclude?

Answer: There are no two students in the class with both the same number of unread emails and the same number of Instagram followers.

The DataFrame survey.groupby(["Unread Emails", "IG Followers"]).count() will have one row for every unique combination of "Unread Emails" and "IG Followers". If two students had the same number of "Unread Emails" and "IG Followers", they would be grouped together, resulting in fewer groups than the total number of students. But since A == B, it indicates that there are as many unique combinations of these two columns as there are rows in the survey DataFrame. Thus, no two students share the same combination of "Unread Emails" and "IG Followers".

Note that if student X has 2 "Unread Emails" and 5 "IG Followers", student Y has 2 "Unread Emails" and 3 "IG Followers", and student Z has 3 "Unread Emails" and 5 "IG Followers", they all have different combinations of "Unread Emails" and "IG Followers", meaning that they’d all be represented by different rows in survey.groupby(["Unread Emails", "IG Followers"]).count(). This is despite the fact that some of their numbers of "Unread Emails" and "IG Followers" are not unique.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 72%.

Problem 4.2

We’d like to find the mean number of Instagram followers of all students in DSC 10. One correct way to do so is given below.

Answer:

Is mean_2 is equal to mean_1? Yes, if both sections have the same number of students, otherwise maybe.

mean_2 is the “mean of means” – it finds the mean number of "IG Followers" for each section, then finds the mean of those two numbers. This is not in general to the overall mean, because it doesn’t consider the fact that Section A may have more students than Section B (or vice versa); if this is the case, then Section A needs to be weighted more heavily in the calculation of the overall mean.

Let’s look at a few examples to illustrate our point. - Suppose Section A has 2 students who both have 10 followers, and Section B has 1 student who has 5 followers. The overall mean number of followers is \frac{10 + 10 + 5}{3} = 8.33.., while the mean of the means is \frac{10 + 5}{2} = 7.5. These are not the same number, so mean_2 is not always equal to mean_1. We can rule out “Yes” as an option. - Suppose Section A has 2 students where one has 5 followers and one has 7, and Section B has 2 students where one has 3 followers and one has 15 followers. Then, the overall mean is \frac{5 + 7 + 3 + 13}{4} = \frac{28}{4} = 7, while the mean of the means is \frac{\frac{5+7}{2} + \frac{3 + 13}{2}}{2} = \frac{6 + 8}{2} = 7. If you experiment (or even write out a full proof), you’ll note that as long as Sections A and B have the same number of students, the overall mean number of followers across their two sections is equal to the mean of their section-specific mean numbers of followers. We can rule out “No” as an option. - Suppose Section A has 2 students who both have 10 followers, and Section B has 3 students who both have 10 followers. Then, the overall mean is 10, and so is the mean of means. So, it’s possible for there to be a different number of students in Sections A and B and for mean_2 to be equal to mean_1. It’s not always, true, though, which is why the answer is “Yes, if both sections have the same number of students, otherwise maybe” and we can rule out the “otherwise no” case.

Difficulty: ⭐️⭐️⭐️⭐️⭐️

The average score on this problem was 15%.

Is mean_3 is equal to mean_1? Yes.

Let’s break down the calculations:

For X: survey.groupby("Section").sum().get("IG Followers") calculates the total number of followers for each section separately. The subsequent .sum() then adds these totals together, providing the total number of followers in the entire class.
For Y: survey.groupby("Section").count().get("IG Followers") counts the number of students in each section. The subsequent .sum() then aggregates these counts, giving the total number of students in the entire class.

Then, mean_3 = X / Y divides the total number of Instagram followers by the total number of students to get the overall average number of followers per student for the entire dataset. This is precisely how mean_1 is calculated. Hence, mean_3 and mean_1 will always be equal, so the answer is “Yes.”

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 58%.

Problem 5

Teresa and Sophia are bored while waiting in line at Bistro and decide to start flipping a UCSD-themed coin, with a picture of King Triton’s face as the heads side and a picture of his mermaid-like tail as the tails side.

Teresa flips the coin 21 times and sees 13 heads and 8 tails. She stores this information in a DataFrame named teresa that has 21 rows and 2 columns, such that:

Then, Sophia flips the coin 11 times and sees 4 heads and 7 tails. She stores this information in a DataFrame named sophia that has 11 rows and 2 columns, such that:

Problem 5.1

Answer: 108

Since we used the argument on="flips, rows from teresa and sophia will be combined whenever they have matching values in their "flips" columns.

For the teresa DataFrame:

There are 13 rows with "Heads" in the "flips" column.
There are 8 rows with "Tails" in the "flips" column.

For the sophia DataFrame:

There are 4 rows with "Heads" in the "flips" column.
There are 7 rows with "Tails" in the "flips" column.

The merged DataFrame will also only have the values "Heads" and "Tails" in its "flips" column. - The 13 "Heads" rows from teresa will each pair with the 4 "Heads" rows from sophia. This results in 13 \cdot 4 = 52 rows with "Heads" - The 8 "Tails" rows from teresa will each pair with the 7 "Tails" rows from sophia. This results in 8 \cdot 7 = 56 rows with "Tails".

Then, the total number of rows in the merged DataFrame is 52 + 56 = 108.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 54%.

Problem 5.2

Suppose we again merge teresa and sophia on the "flips" column. In terms of A, how many rows are in the new merged DataFrame?

Answer: A+1

The additional row in each DataFrame has a unique "flips" value of "Total". When we merge on the "flips" column, this unique value will only create a single new row in the merged DataFrame, as it pairs the "Total" from teresa with the "Total" from sophia. The rest of the rows are the same as in the previous merge, and as such, they will contribute the same number of rows, A, to the merged DataFrame. Thus, the total number of rows in the new merged DataFrame will be A (from the original matching rows) plus 1 (from the new "Total" rows), which sums up to A+1.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 46%.

Problem 6

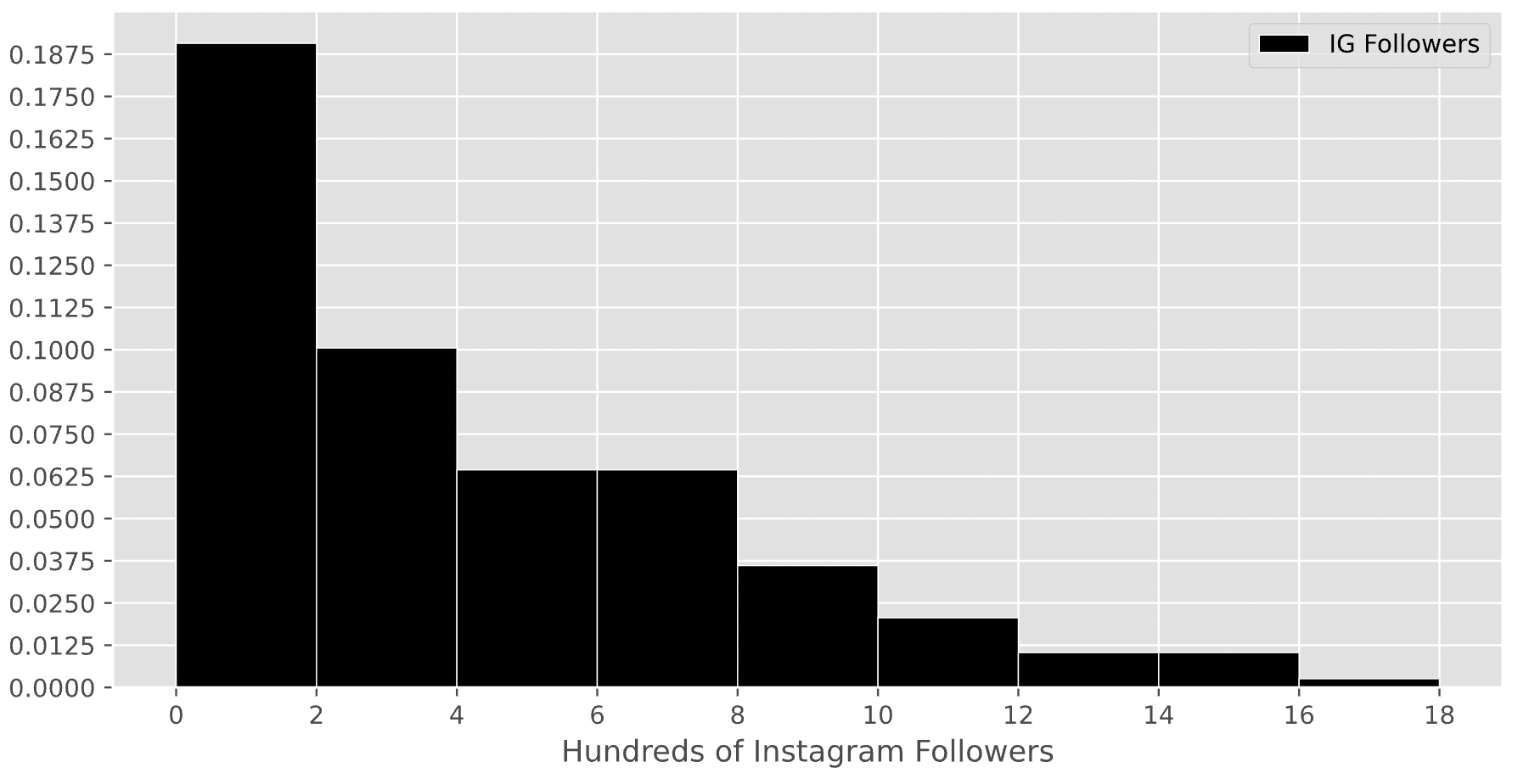
The histogram below displays the distribution of the number of Instagram followers each student has, measured in 100s. That is, if a student is represented in the first bin, they have between 0 and 200 Instagram followers.

Problem 6.1

How many students in DSC 10 have between 200 and 800 Instagram followers? Give your answer as an integer.

Answer: 90

Remember, the key property of histograms is that the proportion of values in a bin is equal to the area of the corresponding bar. To find the number of values in the range 2-8 (the x-axis is measured in hundreds), we’ll need to find the proportion of values in the range 2-8 and multiply that by 200, which is the total number of students in DSC 10. To find the proportion of values in the range 2-8, we’ll need to find the areas of the 2-4, 4-6, and 6-8 bars.

Area of the 2-4 bar: \text{width} \cdot \text{height} = 2 \cdot 0.1 = 0.2

Area of the 4-6 bar: \text{width} \cdot \text{height} = 2 \cdot 0.0625 = 0.125.

Area of the 6-8 bar: \text{width} \cdot \text{height} = 2 \cdot 0.0625 = 0.125.

Then, the total proportion of values in the range 2-8 is 0.2 + 0.125 + 0.125 = 0.45, so the total number of students with between 200 and 800 Instagram followers is 0.45 \cdot 200 = 90.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 49%.

Problem 6.2

Suppose the height of a bar in the above histogram is h. How many students are represented in the corresponding bin, in terms of h?

Hint: Just as in the first subpart, you’ll need to use the assumption from the start of the problem.

Answer: 400 \cdot h

As we said at the start of the last solution, the key property of histograms is that the proportion of values in a bin is equal to the area of the corresponding bar. Then, the number of students represented bar a bar is the total number of students in DSC 10 (200) multiplied by the area of the bar.

Since all bars in this histogram have a width of 2, the area of a bar in this histogram is \text{width} \cdot \text{height} = 2 \cdot h. If there are 200 students in total, then the number of students represented in a bar with height h is 200 \cdot 2 \cdot h = 400 \cdot h.

To verify our answer, we can check to see if it makes sense in the context of the previous subpart. The 2-4 bin has a height of 0.1, and 400 \cdot 0.1 = 40. The total number of students in the range 2-8 was 90, so it makes sense that 40 of them came from the 2-4 bar, since the 2-4 bar takes up about half of the area of the 2-8 range.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 36%.

Problem 7

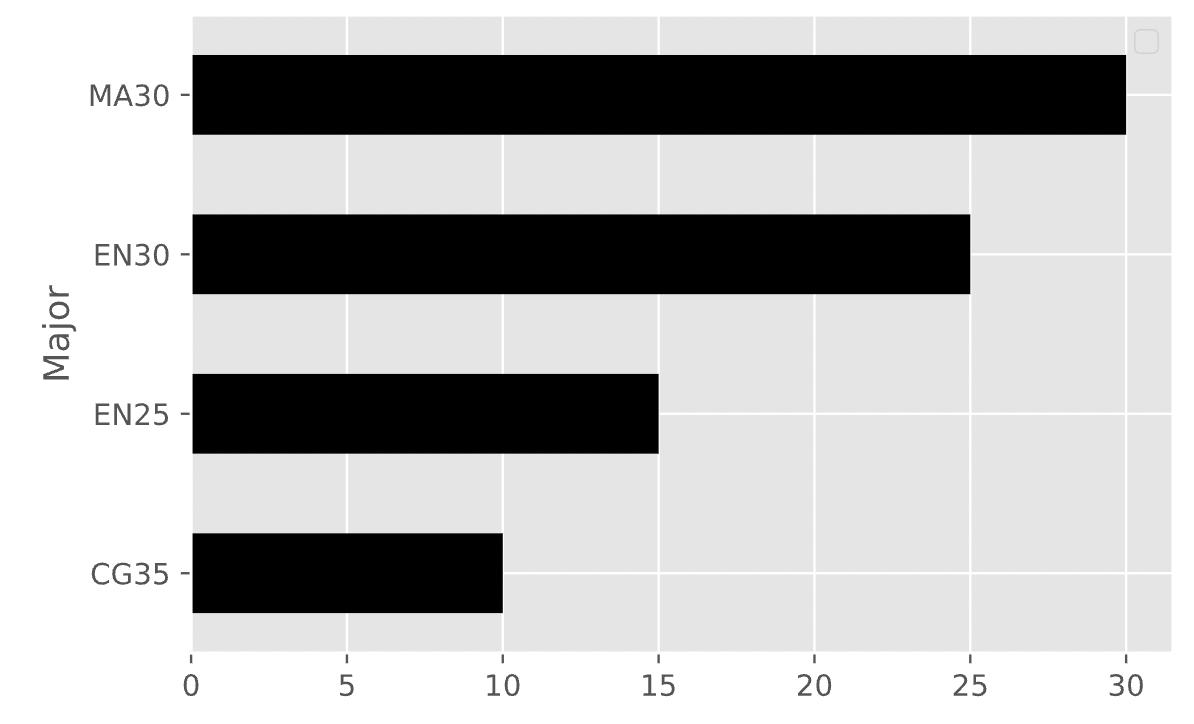
The four most common majors among students in DSC 10 this quarter are "MA30" (Mathematics - Computer Science), "EN30" (Business Economics), "EN25" (Economics), and "CG35" (Cognitive Science with a Specialization in Machine Learning and Neural Computation). We’ll call these four majors “popular majors".

There are 80 students in DSC 10 with a popular major. The distribution of popular majors is given in the bar chart below.

Problem 7.1

Answer: [-4, -3. -2, -1]

Let’s break down the code line by line:

.groupby("Major") will group the survey DataFrame by the "Major" column.
.count() will count the number of students in each major.
.sort_values("College") sort these counts in ascending order using the "College" column (which now contains counts).
.take([-4, -3. -2, -1]) will take the last 4 rows of the DataFrame, which will correspond to the 4 most common majors.
.get("Section") get the "Section" column, which also contains counts.
.plot(kind="barh") will plot these counts in a horizontal bar chart.

The argument we give to take is [-4, -3, -2, -1], because that will give us back a DataFrame corresponding to the counts of the 4 most common majors, with the most common major ("MA30") at the bottom. We want the most common major at the bottom of the Series that .plot(kind="barh") is called on because the bottom row will correspond to the top bar – remember, kind="barh" plots one bar per row, but in reverse order.

Difficulty: ⭐️⭐️⭐️⭐️⭐️

The average score on this problem was 4%.

Problem 7.2

Suppose we select two students in popular majors at random with replacement. What is the probability that both have "EN" in their major code? Give your answer in the form of a simplified fraction.

Answer: \frac{1}{4}

Total number of students in popular majors: 30 + 25 + 15 + 10 = 80
The number of students with "EN" in their major code is the sum of "EN30" and "EN25" students: 25 + 15 = 40

The probability that a single student chosen at random from the popular majors has "EN" in their major code is number of "EN" majors divided by total number of popular majors.

P(\text{one has ``EN"}) = \frac{40}{80} = \frac{1}{2}

Since the students are chosen with replacement, the probabilities remain consistent for each draw. So the probability that both randomly chosen students (with replacement) have "EN" in their major code is

P(\text{both have ``EN"}) = P(\text{one has ``EN"}) \cdot P(\text{one has ``EN"}) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 61%.

Problem 7.3

Suppose we select two students in popular majors at random with replacement. What is the probability that we select one "CG35" major and one "MA30" major (in any order)?

Answer: \frac{3}{32}

The probability of selecting one "CG35" major first and then one "MA30" major is: \frac{10}{80} \cdot \frac{30}{80} = \frac{1}{8} \cdot \frac{3}{8} = \frac{3}{64}
The probability of selecting one "MA30" major first and then one "CG35" major is: \frac{30}{80} \cdot \frac{10}{80} = \frac{3}{8} \cdot \frac{1}{8} = \frac{3}{64}

Since the two events are mutually exclusive (they cannot both happen), we sum their probabilities to get the combined probability of the event occurring in any order:
P(\text{one ``CG35" and one ``MA30"}) = P(\text{``CG35" then ``MA30" OR ``MA30" then ``CG35"}) = P(\text{``CG35 then ``MA30"}) + P(\text{``MA30" then ``CG35"}) = \frac{3}{64} + \frac{3}{64} = \frac{6}{64} = \frac{3}{32}

Difficulty: ⭐️⭐️⭐️⭐️⭐️

The average score on this problem was 18%.

Problem 7.4

Suppose we select k students in popular majors at random with replacement. What is the probability that we select at least one "CG35" major?

Answer: \frac{8^k - 7^k}{8^k}

Of the 80 students in popular majors, 10 are in "CG35". To determine the likelihood of selecting at least one "CG35" major out of k random draws with replacement, we first find the probability of not drawing a "CG35" major in all k attempts by following the steps below:

The probability of not selecting a "CG35" major in one draw is 1 - \frac{10}{80} = 1 - \frac{1}{8} = \frac{7}{8}
The probability of not selecting a "CG35" major in k draws is, then, \frac{7^k}{8^k}, since each draw is independent.

Now, by subtracting this probability from 1, we get the probability of drawing at least one "CG35" major in those k attempts. So, the probability of selecting at least one "CG35" major in k attempts is 1 - \frac{7^k}{8^k} = \frac{8^k}{8^k} - \frac{7^k}{8^k} = \frac{8^k - 7^k}{8^k}

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 58%.

Problem 8

We’d like to select three students at random from the entire class to win extra credit (not really). When doing so, we want to guarantee that the same student cannot be selected twice, since it wouldn’t really be fair to give a student double extra credit.

Fill in the blanks below so that prob_all_unique is an estimate of the probability that all three students selected are in different majors.

Hint: The function np.unique, when called on an array, returns an array with just one copy of each unique element in the input. For example, if vals contains the values 1, 2, 2, 3, 3, 4, np.unique(vals) contains the values 1, 2, 3, 4.

Problem 8.1

Answer: replace=False

Since we want to guarantee that the same student cannot be selected twice, we should sample without replacement.

Difficulty: ⭐️⭐️

The average score on this problem was 77%.

Problem 8.2

Aswer: unique_majors

unique_majors is the array we initialized before running our for-loop to keep track of our results. We’re already given that the first argument to np.append is unique_majors, meaning that in each iteration of the for-loop we’re creating a new array by adding a new element to the end of unique_majors; to save this new array, we need to re-assign it to unique_majors.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 65%.

Problem 8.3

Answer: np.unique(group)

In each iteration of our for-loop, we’re interested in finding the number of unique majors among the 3 students who were selected. We can tell that this is what we’re meant to store in unique_majors by looking at the options in the next subpart, which involve checking the proportion of times that the values in unique_majors is 3.

The majors of the 3 randomly selected students are stored in group, and np.unique(group) is an array with the unique values in group. Then, len(np.unique(group)) is the number of unique majors in the group of 3 students selected.

Difficulty: ⭐️⭐️⭐️⭐️

The average score on this problem was 45%.

Problem 8.4

What could go in blank (d)? Select all that apply. At least one option is correct; blank answers will receive no credit.

Answer: Option 1 only

Let’s break down the code we have so far:

An empty array named unique_majors is initialized to store the number of unique majors in each iteration of the simulation.
The simulation runs 10,000 times, and in every iteration: Three majors are selected at random from the survey dataset without replacement. This ensures that the same item is not chosen more than once within a single iteration. The np.unique function is employed to identify the number of unique majors among the selected three. The result is then appended to the unique_majors array.
Following the simulation, the objective is to determine the fraction of iterations in which all three selected majors were unique. Since the maximum number of unique majors that can be selected in a group of three is 3, the code checks the fraction of times the unique_majors array contains a value greater than 2.

Let’s look at each option more carefully.

Option 1: (unique_majors > 2).mean() will create a Boolean array where each value in unique_majors is checked if it’s greater than 2. In other words, it’ll return True for each 3 and False otherwise. Taking the mean of this Boolean array will give the proportion of True values, which corresponds to the probability that all 3 students selected are in different majors.
Option 2: (unique_majors.sum() > 2) will generate a single Boolean value (either True or False) since you’re summing up all values in the unique_majors array and then checking if the sum is greater than 2. This is not what you want. .mean() on a single Boolean value will raise an error because you can’t compute the mean of a single Boolean.
Option 3: np.count_nonzero(unique_majors > 2).sum() / len(unique_majors > 2) would work without the .sum(). unique_majors > 2 results in a Boolean array where each value is True if the respective simulation yielded 3 unique majors and False otherwise. np.count_nonzero() counts the number of True values in the array, which corresponds to the number of simulations where all 3 students had unique majors. This returns a single integer value representing the count. The .sum() method is meant for collections (like arrays or lists) to sum their elements. Since np.count_nonzero returns a single integer, calling .sum() on it will result in an AttributeError because individual numbers do not have a sum method. len(unique_majors > 2) calculates the length of the Boolean array, which is equal to 10,000 (the total number of simulations). Because of the attempt to call .sum() on an integer value, the code will raise an error and won’t produce the desired result.
Option 4: np.count_nonzero(unique_majors != 3) counts the number of trials where not all 3 students had different majors. When you call .mean() on an integer value, which is what np.count_nonzero returns, it’s going to raise an error.
Option 5: unique_majors.mean() - 3 == 0 is trying to check if the mean of unique_majors is 3. This line of code will return True or False, and this isn’t the right approach for calculating the estimated probability.

Difficulty: ⭐️⭐️⭐️

The average score on this problem was 56%.

Video 🎥

Problem 1

Problem 1.1

Click to view the solution.

Difficulty: ⭐️

Problem 1.2

Click to view the solution.

Difficulty: ⭐️

Problem 1.3

Click to view the solution.

Difficulty: ⭐️

Problem 1.4

Click to view the solution.

Difficulty: ⭐️

Problem 1.5

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️

Problem 1.6

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 1.7

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 2

Problem 2.1

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 2.2

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 2.3

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 2.4

Click to view the solution.

Difficulty: ⭐️⭐️

Problem 2.5

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 3

Problem 3.1

Click to view the solution.

Difficulty: ⭐️

Difficulty: ⭐️⭐️⭐️

Difficulty: ⭐️

Difficulty: ⭐️⭐️

Problem 3.2

Click to view the solution.

Difficulty: ⭐️⭐️

Difficulty: ⭐️⭐️⭐️

Problem 4

Problem 4.1

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 4.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️⭐️

Difficulty: ⭐️⭐️⭐️

Problem 5

Problem 5.1

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 5.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️

Problem 6

Problem 6.1

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️

Problem 6.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️

Problem 7

Problem 7.1

Click to view the solution.

Difficulty: ⭐️⭐️⭐️⭐️⭐️

Problem 7.2

Click to view the solution.

Difficulty: ⭐️⭐️⭐️

Problem 7.3