← return to practice.dsc10.com
Instructor(s): Janine Tiefenbruck
This exam was administered in-person. The exam was closed-notes, except students were provided a copy of the DSC 10 Reference Sheet. No calculators were allowed. Students had 50 minutes to take this exam.
In this exam, you’ll work with a data set representing your phone’s
contact list. contacts is indexed by "Person".
You store each person in your contacts under a unique name.
The columns of contacts are as follows:
"Phone" (str): Your contact’s phone
number, formatted like "xxx-xxx-xxxx", where each
x represents a digit 0 through 9. All of your contacts have
distinct phone numbers.
"Day" (int): The day of the month your
contact was born. Values are 1 through 31.
"Month" (str): The month your contact
was born.
"Year" (int): The year your contact was
born.
"DOB" (str): Your contact’s date of
birth, in the form "MM-DD-YYYY".
The first few rows of contacts are shown below, though
contacts has many more rows than pictured.
Throughout this exam, we will refer to contacts
repeatedly.
Assume that we have already run import babypandas as bpd
and import numpy as np.
Fill in the blanks in the function sum_phone below. This
function should take as input a string representing a phone number,
given in the form "xxx-xxx-xxxx", and return the sum of the
digits of that phone number, as an int.
For example, sum_phone("501-800-3002") should evaluate
to 19.
def sum_phone(phone_number):
total = 0
for digit in phone_number:
if ___(a)___:
___(b)___
return totalAnswer:
digit != "-"total = total + int(digit)digit is a number, and the
only character in the string of the phone_number is the
hyphen (-). For instance, in the given phone number of
"501-800-3002", we want to extract the actual numbers in
the string, without the hyphens. So, because we cannot establish a
numerical value to a hyphen, we exclude it.
The average score on this problem was 34%.
The average score on this problem was 71%.
The first contact in contacts is your friend Calvin, who
has an interesting phone number, with all the digits in descending
order: 987-654-3210. Fill in the blanks below so that each expression
evaluates to the sum of the digits in Calvin’s phone number.
contacts.get("Phone").apply(sum_phone).iloc[___(a)___]Answer: 0
(a) should be filled with 0 because
.iloc[0] refers to the first item in a Series, which
corresponds to Calvin.
The average score on this problem was 89%.
sum_phone(contacts.get("Phone").loc[___(b)___])Answer: "Calvin"
(b) should be filled with "Calvin" because
.loc[] accesses an element of Series by its row label. In
this case, "Calvin" is the index label of the Series
element that contains Calvin’s phone number.
The average score on this problem was 84%.
np.arange(__(c)__,__(d)__,__(e)__).sum() Answer:
(c): 0 or alternate solution 9
(d): 10 or alternate solution
-1
(e): 1 or alternate solution
-1
The expression uses np.arange() to generate a range of
numbers and then sums them up. From the problem, we can see that
Calvin’s phone number includes every digit from 9 to 0, so summing this
is equivalent to summing the digits from 9 down to 0 or from 0 to 9.
np.arange(0, 10, 1) generates [0, 1, 2, 3, 4, 5, 6, 7,
8, 9]. Alternatively, using the numbers in descending order (like the
digits in Calvin’s phone number): np.arange(9, -1, -1)
generates [9, 8, 7, 6, 5, 4, 3, 2, 1, 0]. Both correctly sum up to
45.
The average score on this problem was 74%.
Write a Python expression that evaluates to a DataFrame of only your
contacts whose phone numbers end in "6789".
Note: Do not use slicing, if you know what that is. You must use methods from this course.
Answer:
contacts[contacts.get("Phone").str.contains("6789")] or
contacts[contacts.get("Phone").str.contains("-6789")]
contacts.get("Phone"): retrieves the
"Phone" column from the contacts DataFrame as a
Series..str.contains("6789"): applies a string method that
checks for the presence of the substring "6789" in each
phone number, which could only present in the end of the phone number.
It returns a Boolean Series indicating True for phone numbers containing
this substring.contacts[...]: retrieve all rows where the condition is
True.
The average score on this problem was 63%.
Oh no! A monkey has grabbed your phone and is dialing a phone number by randomly pressing buttons on the keypad, such that each button pressed is equally likely to be any of ten digits 0 through 9.
The monkey managed to dial a ten-digit number and call that number.
What is the probability that the monkey calls one of your contacts? Give
your answer as a Python expression, using the DataFrame
contacts.
Answer:
(contacts.shape[0])/(10**10)
contacts.shape[0]: retrieves the number of rows in the
contacts DataFrame, representing the total number of phone numbers you
have stored in your contacts.10**10: Since the phone number consists of ten digits,
and each digit can be any number from 0 to 9, there are a total of
10**10 possible ten-digit numbers.Given that each digit pressed is equally likely and independent of
others, the likelihood of hitting a specific number from your contacts
by random chance is simply the count of your contacts divided by the
total number of possible combinations (which is
10**10).
The average score on this problem was 43%.
Now, your cat is stepping carefully across the keypad of your phone, pressing 10 buttons. Each button is sampled randomly without replacement from the digits 0 through 9.
You catch your cat in the act of dialing, when the cat has already dialed 987-654. Based on this information, what is the probability that the cat dials your friend Calvin’s number, 987-654-3210? Give your answer as an unsimplified mathematical expression.
Answer: \dfrac{1}{4 \cdot 3 \cdot 2 \cdot 1}
The cat has already dialed “987-654”. Since the first six digits are fixed and chosen without replacement, the only remaining digits to be dialed are 3, 2, 1, and 0. The sequence “3210” must be dialed in that exact order from the remaining digits.
The product of these probabilities gives \dfrac{1}{4 \cdot 3 \cdot 2 \cdot 1}, representing the likelihood of this specific sequence occurring.
The average score on this problem was 55%.
Arya’s phone number has an interesting property: after the area code (the first three digits), the remaining seven numbers of his phone number consist of only two distinct digits.
Recall from the previous question that when the monkey dials a phone number, each digit it selects is equally likely to be any of the digits 0 through 9. Further, when the cat is dialing a phone number, it makes sure to only use each digit once.
You’re interested in estimating the probability that a phone number dialed by the monkey or the cat has exactly two distinct digits after the area code, like Arya’s phone number. You write the following code, which you plan to use for both the monkey and cat scenarios.
digits = np.arange(10)
property_count = 0
num_trials = 10000
for i in np.arange(num_trials):
after_area_code = __(x)__
num_distinct = len(np.unique(after_area_code))
if __(y)__:
property_count = property_count + 1
probability_estimate = property_count / num_trialsFirst, you want to estimate the probability that the
monkey randomly generates a number with only 2 distinct
digits after the area code. What code should be used to fill in blank
(x)?
Answer:
np.random.choice(digits, 7, replace = True) or
np.random.choice(digits, 7)
The code simulates the monkey dialing seven digits where each digit
is selected randomly from the digits 0 through 9, and digits can repeat
(replace = True).
The average score on this problem was 50%.
Next, you want to estimate the probability that the
cat randomly generates a number with only 2 distinct
digits after the area code. What code should be used to fill in blank
(x)?
Answer:
np.random.choice(digits, 7, replace = False)
The code simulates random dialing by a cat without replacement
(replace = False). Each digit from 0 to 9 is used only
once.
The average score on this problem was 52%.
In either case, whether you’re simulating the monkey or the cat, what
should be used to fill in blank (y)?
Answer: num_distinct == 2
This part of the code checks if the number of unique digits in the dialed number is exactly two.
The average score on this problem was 52%.
When you are simulating the cat, what will the value
of probability_estimate be after the code executes?
Answer: 0
Since the cat dials each digit without replacement, it’s impossible
for the dialed number to contain only two distinct digits (as it would
need to repeat some digits to achieve this). Thus, no trial will meet
the condition num_distinct == 2, resulting in a
property_count of 0 and therefore a probability_estimate of 0.
The average score on this problem was 53%.
Suppose Charlie and Norah each have separate DataFrames for their
contacts, called charlie and norah,
respectively. These DataFrames have the same column names and format as
your DataFrame, contacts.
As illustrated in the diagram below, Charlie has 172 contacts in
total, whereas Norah has 88 contacts. 12 of these contacts are shared,
meaning they appear in both charlie and
norah.
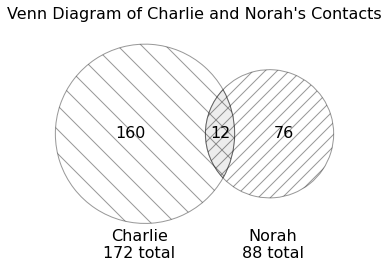
What does the following expression evaluate to?
charlie.merge(norah, left_index=True, right_index=True).shape[0] Answer: 12
The code merges DataFrames charlie and
norah on their indexes, so the resulting DataFrame will
contain one row for every match between their indexes (‘Person’ since
they follow the same format as DataFrame contact). From the
Venn Diagram, we know that Charlie and Norah have 12 contacts in common,
so the resulting DataFrame will contain 12 rows: one row for each shared
contact.
Thus,
charlie.merge(norah, left_index=True, right_index=True).shape[0]
returns the row number of the resulting DataFrame, which is 12.
The average score on this problem was 66%.
One day, when updating her phone’s operating system, Norah
accidentally duplicates the 12 contacts she has in common with Charlie.
Now, the norah DataFrame has 100 rows.
What does the following expression evaluate to?
norah.merge(norah, left_index=True, right_index=True).shape[0] Answer: 24 \cdot 2 + 76 = 124
Since Norah duplicates 12 contacts, the norah DataFrame
now has 76 unique rows + 12 rows + 12 duplicated rows. Note that the
above code is now merging norah with itself on indexes.
After merging, the resulting DataFrame will contain 76 unique rows, as there is only one match for each unique row. As for the duplicated rows, each row can match twice, and we have 24 rows. Thus the resulting DataFrame’s row number = 76 + 2 \cdot 24 = 124.
For better understanding, imagine we have a smaller DataFrame
nor with only one contact Jim. After duplication, it will
have two identical rows of Jim. For easier explanation, let’s denote the
original row Jim1, and duplicated row Jim2. When merging Nor with
itself, Jim1 can be matched with Jim1 and Jim2, and Jim2 can be matched
with Jim1 and Jim2, resulting $= 2 = 4 $ number of rows.
The average score on this problem was 3%.
Recall from the data description that the "DOB" column
in contacts contains the date of birth of everyone in your
contacts list, as a string formatted like "MM-DD-YYYY".
Looking at the calendar, you see that today’s date is May 3rd, 2024,
which is "05-03-2024".
Using today’s date, fill in the blanks in the function
age_today so that the function takes as input someone’s
date of birth, as a string formatted like "MM-DD-YYYY", and
returns that person’s age, as of today.
def age_today(dob):
dob = dob.split("-")
month = ___(a)___ # the month, as an int
day = ___(b)___ # the day, as an int
year = ___(c)___ # the year, as an int
if ___(d)___:
return 2024 - year
return 2024 - year - 1Answer:
int(dob[0])int(dob[1])int(dob[2])(month < 5) or (month == 5 and day <= 3).split() method divides a string into a list based on delimiter. In
this probelm, dob.split("-") returns a list of substrings
that were separated by hyphens in the original string formatted like
"MM-DD-YYYY". Thus, after using the .split("-"), the resulting list will be formatted like[“MM”,
“DD”, “YYYY”]. Thus, we can access month, day, year by its position in
the list dob.
Note that the comment asks month, day, year as int, do we need to
convert them from string to int datatype, by using int(). Thus, we have
month = int(dob[0]), day = int(dob[1]),
year = int(dob[2]). This is for us to calculate age later
by comparing month and day numebrs.
Then to calculate the age of the person given today is “05-03-2024”,
we can use 2024-year. But if a person is born after May
3rd, then they are techinically 1 year younger than that, so we should
use 2024-year-1. Thus in the if statment, we use
(month < 5) or (month == 5 and day <= 3) to compare
if the person is born in January, February, March, April or one of the
first three days of May.
The average score on this problem was 59%.
Write a Python expression that evaluates to the average age of all of your contacts, as of today.
Answer:
contacts.get("DOB").apply(age_today).mean()
contacts.get("DOB") gets the column ‘DOB’ column in
contacts DataFrame as a series.
.apply(age_today) applies the function
age_today to each element in the series to calculate age,
and returns a series of ages of all contacts.
.mean() calculates the average of the series, giving the
average age of all contacts.
The average score on this problem was 80%.
You wonder if any of your friends have the same birthday, for example
two people both born on April 3rd. Fill in the blanks below so that the
given expression evaluates to the largest number of people in
contacts who share the same birthday.
Note: People do not need to be born in the same year to share a birthday!
contacts.groupby(___(a)___).___(b)___.get("Phone").___(c)___["Month", "Day"]count()max().groupby(["Month", "Day"]).count() groups the DataFrame
contacts by each unique combination of ‘Month’ and ‘Day’ (birthday) and
then counts the number of rows in each group (i.e. number of people born
on that date).
.get('Phone') gets a series which contains the counts of
people born on each date, and .max() finds the largest
number of people sharing the same birthday.
The average score on this problem was 72%.
Consider the histogram generated by the following code.
contacts.plot(kind="hist", y="Day", density=True, bins=np.arange(1, 33))Which of the following questions would you be able to answer from this histogram? Select all that apply.
How many of your contacts were born on a Monday?
How many of your contacts were born on January 1st?
How many of your contacts were born on the first day of the month?
How many of your contacts were born on the last day of the month?
Answer: Option 3: How many of your contacts were born on the first day of the month?
contacts.plot(kind="hist", y="Day", density=True, bins=np.arange(1, 33))
generates a histogram that visualizes the distribution of values in the
‘Day’ column of the contacts DataFrame.
bins=np.arange(1, 33) creates the bins
[1,2], [2,3], ..., [31,32]. Each bar in the histogram
represents the density of a day.
We can answer the question “How many of your contacts were born on the first day of the month?” by checking the bar containing the first day (the first bar).
However, the histogram doesn’t contain information of day of the week or month, so it can’t answer questions in options 1 or 2.
We also can’t choose option 4, because we have months with varying numbers of days (28, 29, 30, or 31). For months with 31 days, we know for sure it’s the last day of the month. For bars with 28, 29, and 30 days, we won’t be able to tell which proportion of days are the last day of the month since months with 31 days will have a count in all the previous number of days.
The average score on this problem was 80%.
After looking at the distribution of "Day" for your
contacts, you wonder how that distribution might look for other groups
of people.
In this problem, we will consider the distribution of day of birth (just the day of the month, not the month or year) for all babies born in the year 2023, under the assumption that all babies born in 2023 were equally likely to be born on each of the 365 days of the year.
The density histogram below shows this distribution.
Note: 2023 was not a leap year, so February had 28 days.
What is height (a)?
\dfrac{1}{28}
\dfrac{28}{365}
\dfrac{12 \cdot 28}{365}
\dfrac{1}{12}
\dfrac{12}{365}
1
Answer: \dfrac{12}{365}
2023 was not a leap year, so there are in total 365 days, and February only has 28 days. All the months have at least 28 days, so in bin [1,29], there are 12 * 28 data values. And, all the months other than February have 29th and 30th days, so there are 2 * 11 data values in bin [29,31]. Lastly, there are 7 months with 31 days, so there are 7 data values in bin [31,32].
There are in total 365 data values, so the proportion of data points falling into bin [1,29] =\dfrac{12 \cdot 28}{365}. Thus, the area of the bar of bin [1,29] = \dfrac{12 \cdot 28}{365}. Area = Height * Width, width of the bin is 28, so height(a) = \dfrac{12 \cdot 28}{365 \cdot 28} = \dfrac{12}{365}.
The average score on this problem was 38%.
Express height (b) in terms of height
(a).
\text{(b)} = \dfrac{7}{12} \cdot \text{(a)}
\text{(b)} = \dfrac{27}{28} \cdot \text{(a)}
\text{(b)} = \dfrac{28}{29} \cdot \text{(a)}
\text{(b)} = \dfrac{11}{12} \cdot \text{(a)}
\text{(b)} = \dfrac{7}{11} \cdot \text{(a)}
\text{(b)} = \dfrac{12 \cdot 28}{365} \cdot \text{(a)}
Answer: \text{(b)} = \dfrac{11}{12} \cdot \text{(a)}
Similarly, height(b) = \dfrac{2 \cdot 11}{365 \cdot 2} = \dfrac{11}{365} = \dfrac{11}{12} \cdot \dfrac{12}{365}.
The average score on this problem was 43%.