
← return to practice.dsc10.com
Instructor(s): Janine Tiefenbruck
This exam was administered in-person. The exam was closed-notes, except students were provided a copy of the DSC 10 Reference Sheet. No calculators were allowed. Students had 3 hours to take this exam.
Here’s a walkthrough video of Problems 6-9, and here’s a walkthrough video of Problems 10-14.
The DataFrame games contains information about a sample
of popular games, including board games, dice games, and card games. The
data comes from Board Game Geek, a popular website and vibrant online
community for game enthusiasts.
The columns of games are as follows.
"Name" (str): The name of the game."Mechanics" (str): A sequence of
descriptors for how the game is played. A game can have several
descriptors, each of which is separated by a comma."Domains" (str): A sequence of domains to
which the game belongs. A game can belong to multiple domains."Play Time" (int): The average play time
of the game, in minutes, as suggested by the game’s creators."Complexity" (float): The average
complexity of the game, on a scale of 1 to 5 points, as reported by
Board Game Geek community members."Rating" (str): The average rating of the
game, on a scale of 1 to 10 points, as rated by Board Game Geek
community members. Note that while this data should be numerical, it is
actually stored as a string, because some entries use a comma in place
of a decimal point. For example 8,79 actually represents the number
8.79."BGG Rank" (int): The rank of the game in
Board Game Geek’s database. The formula for how this rank is calculated
is not publicly known, but it likely includes many factors, such as
"Rating", number of registered owners of the game, and
number of reviews.The first few rows of games are shown below (though
games has many more rows than pictured here).

Throughout this exam, we will refer to games repeatedly. Assume that
we have already run import babypandas as bpd and
import numpy as np.
Let’s start by correcting the data in the "Rating"
column. All the values in this column are strings of length 4. In
addition, some strings use commas in place of a dot to represent a
decimal point. Select the options below that evaluate to a Series
containing the values in the "Rating" column, appropriately
changed to floats.
Note: The Series method .str.replace
uses the string method .replace on every string in a
Series.
float(games.get("Rating").str.replace(",", "."))
games.get("Rating").str.replace(",", ".").apply(float)
games.get("Rating").str.replace(",", "").apply(int)/100
games.get("Rating").str.replace(",", "").apply(float)
Important! For the rest of this exam, we will assume
that the values in the "Rating" column have been correctly
changed to floats.
Answer: Option 2
Option 1: Let’s look at the code piece by piece to
understand why this does not work. games.get("Rating")
gives you the column "Rating" as a Series. As per the note,
.str.replace(",", ".") can be used on a Series, and will
replace all commas with periods. The issue is with the use of the
float function; the float function can convert
a single string to a float, like float("3.14"), but not an
entire Series of floats. This will cause an error making this option
wrong.
Option 2: Once again we are getting
"Rating" as a Series and replacing the commas with periods.
We then apply float() to the Series, which will
successfully convert all of the values into floats.
Option 3: This piece of code attempts to replace
commas with nothing, which is correct for values using commas as decimal
separators. However, this approach ignores values that use dots as
decimal separators. Something like
games.get("Rating").str.replace(",", "").str.replace(".", "").apply(int)/100
could correct this mistake.
Option 4: Again, we are getting
"Rating" as a Series and replacing the commas with an empty
string. The values inside of "Rating" are then converted to
floats, which is fine, but remember, that the numbers are 100 times too
big. This means we have altered the actual value inappropriately, which
makes this option incorrect.
The average score on this problem was 67%.
You are unsure whether it would make sense to use
"BGG Rank" as the index of the games
DataFrame, because you are unsure whether this column has duplicate
values. Perhaps, for example, two games are tied and both have a rank of
6.
Select all of the expressions below that evaluate to True when the
"BGG Rank" column could be used as the index (no
duplicates), and False when it could not be used as the index
(duplicates). In other words, these are the expressions that can be used
to detect the presence of duplicate values.
(games.get("BGG Rank") - np.arange(games.shape[0])).max() == 1
games.groupby("BGG Rank").count().get("Name").max() == 1
games.shape[0] - len(np.unique(games.get("BGG Rank"))) == 0
games.get("BGG Rank").max() - games.shape[0] == 0
Note: We will not set the index of
games, instead we’ll leave it with the default index.
Answer: Options 2 and 3
Option 2:
games.groupby(“BGG Rank”).count() gets all of the unique
“BGG Rank”’s and puts them into the index. Then by using
the aggregate function .count() we are able to turn all the
remaining columns into the number of times each “BGG Rank”
appears. Since all of the columns are the same we just need to get one
of them to access the counts. In this case we get the column “Name” by
doing .get(“Name”). Finally, when we do
.max() == 1 we are checking to see if the maximum count for
the number of unique “BGG Rank”’s is one, which would mean
there are no duplicates.
Option 3: Let’s work from the inside out for this
line of code: len(np.unique(games.get(“BGG Rank”))). Like
all the others we are getting a Series of “BGG Rank”.
np.unique() gives us an array with unique elements inside
of the Series. When we do len() we are figuring out how
many unique elements there are inside of “BGG Rank”. Recall
games.shape[0] gets us the number of rows in
games. This means that we are trying to see if the number
of rows is the same as the number of unique elements inside of
“BGG Rank”, and if they are then that means they are all
unique and should equal 0.
Option 1: games.get(“BGG Rank”) will
get you a Series of the “BGG Rank” column.
np.arange(games.shape[0]) will create a numpy array that
will go from zero to games.shape[0], which is the number of
rows in the games DataFrame. So it would look something
like: arr([0, 1, 2, . . ., n]), where n is the
number of rows in games. By doing:
games.get(“BGG Rank”) - np.arange(games.shape[0]) one is
decreasing each rank by an increasing factor of one each time. This
essentially gives a Series of numbers, but it doesn’t actually have
anything to do with uniqueness. We are simply finding if the difference
between “BGG Rank” and the numpy array leads to a maximum
of 1. So although the code works it does not tell us if there are
duplicates.
Option 4: games.get(“BGG Rank”).max()
will give us the maximum element inside of “BGG Rank”.
Note, games.shape[0] gets us the number of rows in
games. We should never make assumptions about what is
inside of “BGG Rank”. This means we don’t know if the
values line up nicely like: 1, 2, 3, . . . games.shape[0],
so the maximum element could be unique, but be bigger than
games.shape[0]. Knowing this, when we do the whole line for
Option 4 it is not guaranteed to be zero when “BGG Rank” is
unique or not, so it does not detect duplicates.
The average score on this problem was 76%.
Notice that "Strategy Games" and
"Thematic Games" are two of the possible domains, and that
a game can belong to multiple domains.
Define the variables strategy and thematic follows.
strategy = games.get("Domains").str.contains("Strategy Games")
thematic = games.get("Domains").str.contains("Thematic Games")What is the data type of strategy?
bool
str
Series
DataFrame
Answer: Series
strategy will give you a Series. This is
because games.get(“Domains”) will give you one column, a
Series, and then
.str.contains(“Strategy Games”) will convert those values
to True if it contains that string and False
otherwise, but it will not actually change the Series to a
DataFrame, a bool, or a str.
The average score on this problem was 81%.
Suppose we randomly select one of the "Strategy Games"
from the games DataFrame.
What is the probability that the randomly selected game is
not also one of the "Thematic Games"?
Write a single line of Python code that evaluates to this probability,
using the variables strategy and thematic in
your solution.
Note: For this question and others that require one line of code, it’s fine if you need to write your solution on multiple lines, as long as it is just one line of Python code. Please do write on multiple lines to make sure your answer fits within the box provided.
Answer:
(games[(strategy == True) & (thematic == False)].shape[0] / games[strategy == True].shape[0])
or
1 - games[strategy & thematic].shape[0] / games[strategy].shape[0]
The problem is asking us to find the probability that a selected game
from “Strategy Games” will not be in
“Thematic Games”. Recall that this is the probability that
given “Strategy Games” will it not be in
“Thematic Games”, which would look like this:
P(“Thematic Games”
Compliment|“Strategy Games”). This means the formula would
look like: (“Thematic Games” Compliment
and
“Strategy Games”)/“Strategy Games”
This means one possible solution for this would be:
(games[(strategy == True) & (thematic == False)].shape[0] / games[strategy == True].shape[0]
This solution works because we are following the formula to find the
probability of thematic complement and strategy games over the number of
times “Strategy Games” are True. Doing
games[query_condition] gives us the games
DataFrame where strategy == True and
thematic == False. Another important thing is that for
(baby)pandas we always use the keyword & and not
and. Note that we are using .shape[0] to get
the number of rows or times that True shows up for
“Strategy Games” and the number of rows or times that
False shows up for “Thematic Games”
Compliment.
Another possible strategy would be using the complement rule: Which
would be: P(“Thematic Games” Compliment) = 1 -
P(“Thematic Games”). This would lead you to an answer like:
(1 - games[strategy & thematic].shape[0]) / games[strategy].shape[0].
games[strategy & thematic].shape[0]) finds you the
probability of P(“Thematic Games”), so when plugged into
the equation above we are able to find P(“Thematic Games”
Compliment).
The average score on this problem was 43%.
Many of the games in the games DataFrame belong to more
than one domain. We want to identify the number of games that belong to
only one domain. Select all of the options below that would correctly
calculate the number of games that belong to only one domain.
Hint: Don’t make any assumptions about the possible
domains.
(games.get("Domains").str.split(" ").apply(len) == 2).sum()
(games.get("Domains").apply(len) == 1).sum()
(games[games.get("Domains").str.split(",").apply(len) == 1].groupby("Domains").count().get("Name").sum())
games[games.get("Domains").str.split(",").apply(len) == 1].shape[0]
Answer: Options 3 and 4
Let’s take a closer look at why Option 3 and Option 4 are correct.
Option 3: Option 3 first queries the
games DataFrame to only keep games with one
“Domains”.
games.get(“Domains”).str.split(“,”).apply(len) == 1 gets
the “Domains” column and splits all of them if they contain
a comma. If the value does have a comma then it will create a list. For
example let’s say the domain was
“Strategy Games”, “Thematic Games” then after doing
str.split(“,”) we would have the list:
[“Strategy Games”, “Thematic Games”]. Any row with a
list will evaluate to False. This means we are
only keeping values where there is one domain. The next
part .groupby(“Domains”).count().get(“Name”).sum() makes a
DataFrame with an index of the unique domains and the number of times
those appear. Note that all the other columns: “Name”,
“Mechanics”, “Play Time”,
“Complexity”, “Rating”, and
“BGG Rank” now evaluate to the same thing, the number of
times a unique domain appears. That means by doing
.get(“Name”).sum() we are adding up all the number of times
a unique domain appears, which would get us the number of games that
belong to only one domain.
Option 4: Option 4 starts off exactly like Option 3,
but instead of doing .groupby() it gets the number of rows
using .shape[0], which will give us the number of games
that belong to only one domain.
Option 1: Let’s step through why Option 1 is
incorrect.
games.get(“Domains”).str.split(“ ”).apply(len) == 2.sum()
gives you a Series of the “Domains” column,
then splits each domain by a space. We then get the length of that
list, check if the length is equal to 2, which would mean
there are two elements in the list, and finally get the sum
of all elements in the list who had two elements because of the split.
Remember that True evaluates to 1 and False
evaluates to 0, so we are getting the number of elements that were split
into two. It does not tell us the number of games that belong to only
one domain.
Option 2: Let’s step through why Option 2 is also
incorrect. (games.get(“Domains”).apply(len) == 1).sum()
checks to see if each element in the column “Domains” has
only one character. Remember when you apply len() to a
string then we get the number of characters in that string. This is
essentially counting the number of domains that have 1 letter. Thus, it
does not tell us the number of games that belong to only one domain.
The average score on this problem was 86%.
We want to create a bootstrapped 95% confidence interval for the
median "Complexity" of all cooperative games, given a
sample of 100 cooperative games.
Suppose coop_sample is a DataFrame containing 100 rows
of games, all of which are cooperative games. We’ll calculate the
endpoints left and right of our bootstrapped
95% confidence interval as follows.
medians = np.array([])
for i in np.arange(10000):
resample = coop_sample.sample(100, replace=True)
median = np.median(resample.get("Complexity"))
medians = np.append(medians, median)
left = np.percentile(medians, 2.5)
right = np.percentile(medians, 97.5)Now consider the interval defined by the endpoints
left_2 and right_2, calculated as follows.
medians_2 = np.array([])
for i in np.arange(10000):
shuffle = coop_sample.assign(shuffle=
np.random.permutation(coop_sample.get("Complexity")))
resample_2 = shuffle.sample(100, replace=True)
median_2 = np.median(resample_2.get("shuffle"))
medians_2 = np.append(medians_2, median_2)
left_2 = np.percentile(medians_2, 2.5)
right_2 = np.percentile(medians_2, 97.5)Which interval should be wider, [left, right] or
[left_2, right_2]?
[left, right]
[left_2, right_2]
Both about the same.
Answer: Both about the same.
It’s important to understand what each code block above is doing in
order to answer this question. Let’s take a look at the original
medians code. We are sampling from the
coop_sample to create a shuffled coop_sample,
we then get the median of the column “Complexity” and append it to the
medians array. Finally, we find the left and right
percentiles of the medians array.
Now we will look at what medians_2 is doing. It looks
like we are adding a new column called “shuffle” to
coop_sample. The column “shuffle” is a
shuffled version of “Complexity”. Then we are taking the
shuffle DataFrame with the “shuffle” column
and sampling from “shuffle” to randomize it again. Then we
get the median of this shuffled column and find its percentiles.
Essentially, both of these blocks of code are taking the
“Complexity” column, shuffling it, finding the median of
the shuffled column, and then finding the confidence interval. Since it
is being done on the same column and in basically the same way both
intervals [left, right] and [left_2, right_2]
are about the same.
The average score on this problem was 77%.
As in the previous question, let coop_sample be a sample
of 100 rows of games, all corresponding to cooperative games.
Define samp and resamp as follows.
samp = coop_sample.get("Complexity")
resamp = coop_sample.sample(100, replace=True).get("Complexity")Which of the following statements could evaluate to True? Select all that are possible.
len(samp.unique()) < len(resamp.unique())
len(samp.unique()) == len(resamp.unique())
len(samp.unique()) > len(resamp.unique())
Answer: Options 2 and 3
Option 2: This is correct because it is possible for
resamp to be shuffled in such a way that the number of
unique elements are not the same.
Option 3: This is correct because it is possible for
resamp to pull the same values more often making it less
unique than samp.
Option 1: The reason that this is incorrect is
because samp.unique() has the most possible unique elements
inside of it. When we shuffle it using
coop_sample.sample(100, replace = True) we could pull the
same value multiple times, making it less unique.
The average score on this problem was 91%.
Which of the following statements could evaluate to True? Select all that are possible.
np.count nonzero(samp == 1) < np.count nonzero(resamp == 1)
np.count nonzero(samp == 1) == np.count nonzero(resamp == 1)
np.count nonzero(samp == 1) > np.count nonzero(resamp == 1)
Answer: Options 1, 2, and 3
Option 1: It might be helpful to recall what exactly
the column “Complexity” holds. In this case it holds the
average complexity of the game on a scale of 1 to 5. The code is trying
to find if the number of ones in samp and
resamp are different. It is possible that when shuffling
due to replace = True that resamp has more
ones inside of it than samp.
Option 2: Once again it is possible that when
shuffled resamp has the same number of ones as
samp does.
Option 3: When we shuffle coop_sample
there is no guarantee that one will sample more ones and instead other
averages could be selected. This means it is possible for the number of
ones in samp can be greater than the number of ones in
resamp.
The average score on this problem was 83%.
Which of the following statements could evaluate to True? Select all that are possible.
samp.min() < resamp.min()
samp.min() == resamp.min()
samp.min() > resamp.min()
Answer: Options 1 and 2
Option 1: It is possible when shuffled that
samp’s original minimum is never sampled, making
resamp’s minimum to be greater than samp’s
min.
Option 2:: If samp’s original min is
sampled then it will be the same minimum that appears inside of
resamp.
Option 3: It is impossible for resamp’s
minimum to be less than samp’s minimum. This is because all
of resamp’s values come from samp. That means
there cannot be a smaller average inside of resamp that
never appears in samp.
The average score on this problem was 83%.
Which of the following statements could evaluate to True? Select all that are possible.
np.std(samp) < np.std(resamp)
np.std(samp) == np.std(resamp)
np.std(samp) > np.std(resamp)
Answer: Options 1, 2, and 3
Option 1: np.std() gives us the
standard deviation of the array we give it. When we do
np.std(samp) we are finding the standard deviation of
“Complexity”. When we do np.std(resamp) we are
finding the standard deviation of “Complexity”, which may
grab values multiple times. Since we are grabbing values multiple times
it is possible to have a standard deviation become smaller if we
continuously grab smaller values.
Option 2: If the resamp gets us the
same values as samp we would end up with the same standard
deviation, which would make
np.std(samp) == np.std(resamp).
Option 3: Similar to Option 1, we may grab many values which are on the larger end, which could increase our standard deviation.
The average score on this problem was 79%.
Choose the best tool to answer each of the following questions. Note the following:
Are strategy games rated higher than non-strategy games?
Hypothesis testing
Permutation testing
Bootstrapping
Answer: Permutation testing
Recall that we use a permutation test when we want to determine if two samples are from the same population. The question is asking if “strategy games” are rated higher than “non-strategy games” meaning we have two samples and want to know if they come from the same or different rating populations.
We would not use hypothesis testing here because we are not trying to quantify how weird a test statistic between strategy games and non-strategy games.
We would not use bootstrapping here because we are not given a single sample that we want to re-sample from.
The average score on this problem was 58%.
What is the mean complexity of all games?
Hypothesis testing
Permutation testing
Bootstrapping
Answer: Bootstrapping
Bootstrapping is the act of resampling from a sample. We use bootstrapping because the original sample looks like the population, so by resampling the sample we are able to quantify our uncertainty of the mean complexity of all games. We can use bootstrapping to approximate the distribution of the sample statistic, which is the mean.
We would not use hypothesis testing here because we do not have the population distribution or a sample to test with.
We would not use permutation testing here because we are not trying to find if two samples are from the same population.
The average score on this problem was 89%.
Are there an equal number of cooperative and non-cooperative games?
Hypothesis testing
Permutation testing
Bootstrapping
Answer: Hypothesis Testing
Recall hypothesis tests quantify how “weird” a result is. We use it when we have a population distribution and one sample and we are trying to see if that sample was drawn from the population. In this instance we are trying to find if there are an equal number of cooperative and non-cooperative games. The population distribution is our DataFrame and we are trying to see if the cooperative games and non-cooperative games in our sample come from the same population.
We would not use permutation testing here because there is no numerical data in the column, and it can be answered by just the column of categories.
We would not use bootstrapping because we are not re-sampling from the sample we are given to find a test statistic.
The average score on this problem was 75%.
Are games with more than one domain more complex than games with one domain?
Hypothesis testing
Permutation testing
Bootstrapping
Answer: Permutation testing
Once again we would use permutation testing to solve this problem because we have two samples: games with more than one domain and games with one domain. We do not know the population distribution.
We would not use hypothesis testing because we were not given a population distribution to test the sample against.
We would not use bootstrapping because we are not re-sampling from the sample to find a test statistic.
The average score on this problem was 72%.
We use the regression line to predict a game’s "Rating"
based on its "Complexity". We find that for the game
Wingspan, which has a "Complexity" that is 2
points higher than the average, the predicted "Rating" is 3
points higher than the average.
What can you conclude about the correlation coefficient r?
r < 0
r = 0
r > 0
We cannot make any conclusions about the value of r based on this information alone.
Answer: r > 0
To answer this problem, it’s useful to recall the regression line in standard units:
\text{predicted } y_{\text{(su)}} = r \cdot x_{\text{(su)}}
If a value is positive in standard units, it means that it is above
the average of the distribution that it came from, and if a value is
negative in standard units, it means that it is below the average of the
distribution that it came from. Since we’re told that Wingspan
has a "Complexity" that is 2 points higher than the
average, we know that x_{\text{(su)}}
is positive. Since we’re told that the predicted "Rating"
is 3 points higher than the average, we know that \text{predicted } y_{\text{(su)}} must also
be positive. As a result, r must also
be positive, since you can’t multiply a positive number (x_{\text{(su)}}) by a negative number and end
up with another positive number.
The average score on this problem was 74%.
What can you conclude about the standard deviations of “Complexity” and “Rating”?
SD of "Complexity" < SD of "Rating"
SD of "Complexity" = SD of "Rating"
SD of "Complexity" > SD of "Rating"
We cannot make any conclusions about the relationship between these two standard deviations based on this information alone.
Answer: SD of "Complexity" < SD of
"Rating"
Since the distance of the predicted "Rating" from its
average is larger than the distance of the "Complexity"
from its average, it might be reasonable to guess that the values in the
"Rating" column are more spread out. This is true, but
let’s see concretely why that’s the case.
Let’s start with the equation of the regression line in standard
units from the previous subpart. Remember that here, x refers to "Complexity" and
y refers to "Rating".
\text{predicted } y_{\text{(su)}} = r \cdot x_{\text{(su)}}
We know that to convert a value to standard units, we subtract the value by the mean of the column it came from, and divide by the standard deviation of the column it came from. As such, x_{\text{(su)}} = \frac{x - \text{mean of } x}{\text{SD of } x}. We can substitute this relationship in the regression line above, which gives us
\frac{\text{predicted } y - \text{mean of } y}{\text{SD of } y} = r \cdot \frac{x - \text{mean of } x}{\text{SD of } x}
To simplify things, let’s use what we were told. We were told that
the predicted "Rating" was 3 points higher than average.
This means that the numerator of the left side, \text{predicted } y - \text{mean of } y, is
equal to 3. Similarly, we were told that the "Complexity"
was 2 points higher than average, so x -
\text{mean of } x is 2. Then, we have:
\frac{3}{\text{SD of } y} = \frac{2r}{\text{SD of }x}
Note that for convenience, we included r in the numerator on the right-hand side.
Remember that our goal is to compare the SD of "Rating"
(y) to the SD of
"Complexity" (x). We now
have an equation that relates these two quantities! Since they’re both
currently on the denominator, which can be tricky to work with, let’s
take the reciprocal (i.e. “flip”) both fractions.
\frac{\text{SD of } y}{3} = \frac{\text{SD of }x}{2r}
Now, re-arranging gives us
\text{SD of } y \cdot \frac{2r}{3} = \text{SD of }x
Since we know that r is somewhere
between 0 and 1, we know that \frac{2r}{3} is somewhere between 0 and \frac{2}{3}. This means that \text{SD of } x is somewhere between 0 and
two-thirds of the value of \text{SD of }
y, which means that no matter what, \text{SD of } x < \text{SD of } y.
Remembering again that here "Complexity" is our x and "Rating" is our y, we have that the SD of
"Complexity" is less than the SD of
"Rating".
The average score on this problem was 42%.
Suppose that for children’s games, "Play Time" and
"Rating" are negatively linearly associated due to children
having short attention spans. Suppose that for children’s games, the
standard deviation of "Play Time" is twice the standard
deviation of "Rating", and the average
"Play Time" is 10 minutes. We use linear regression to
predict the "Rating" of a children’s game based on its
"Play Time". The regression line predicts that Don’t
Break the Ice, a children’s game with a "Play Time" of
8 minutes will have a "Rating" of 4. Which of the following
could be the average "Rating" for children’s games?
2
2.8
3.1
4
Answer: 3.1
Let’s recall the formulas for the regression line in original units,
since we’re given information in original units in this question (such
as the fact that for a "Play Time" of 8
minutes, the predicted "Rating" is 4
stars). Remember that throughout this question, "Play Time"
is our x and "Rating" is
our y.
The regression line is of the form y = mx + b, where
m = r \cdot \frac{\text{SD of } y}{\text{SD of }x}, b = \text{mean of }y - m \cdot \text{mean of } x
There’s a lot of information provided to us in the question – let’s think about what it means in the context of our xs and ys.
Given all of this information, we need to find possible values for the \text{mean of } y. Substituting our known values for m and b into y = mx + b gives us
y = \frac{r}{2} x + \text{mean of }y - 5r
Now, using the fact that if if x = 8, the predicted y is 4, we have
\begin{align*}4 &= \frac{r}{2} \cdot 8 + \text{mean of }y - 5r\\4 &= 4r - 5r + \text{mean of }y\\ 4 + r &= \text{mean of} y\end{align*}
Cool! We now know that the \text{mean of } y is 4 + r. We know that r must satisfy the relationship -1 \leq r < 0. By adding 4 to all pieces of this inequality, we have that 3 \leq r + 4 < 4, which means that 3 \leq \text{mean of } y < 4. Of the four options provided, only one is greater than or equal to 3 and less than 4, which is 3.1.
The average score on this problem was 55%.
The function perm_test should take three inputs:
df, a DataFrame.labels, a string. The name of a column in df that
contains two distinct values, which signify the groups in a permutation
test.data, a string. The name of a column in df that
contains numerical data.The function should return an array of 1000 simulated differences of group means, under the assumption of the null hypothesis in a permutation test, namely that data in both groups come from the same population.
The smaller of the two group labels should be first in the
subtraction. For example, if the two values in the labels
column are "dice game" and "card game", we
would compute the difference as the mean of the "card game"
group minus the mean of the "dice game" group, because
"card game" comes before "dice game"
alphabetically. Note that groupby orders
the rows in ascending order by default.
An incorrect implementation of perm_test is provided
below.
1 def perm_test(df, labels, data):
2 diffs = np.array([])
3 for i in np.arange(1000):
4 df.assign(shuffled=np.random permutation(df.get(data)))
5 means = df.groupby(labels).mean().get(data)
6 diff = means.iloc[0] - means.iloc[1]
7 diffs = np.append(diffs, diff)
8 return diffsThree lines of code above are incorrect. Your job is to identify which lines of code are incorrect, and describe briefly in English how you would fix them. You don’t need to explain why the current code is wrong, just how to fix it.
The first line that is incorrect is line number: _______
Explain in one sentence how to change this line. Do not write code.
Answer: Line 4; We need to save this as
df.
Recall that df.assign() does not save the added column
to the original df, which means that we need to save line 4
to a variable called df.
The average score on this problem was 55%.
The second line that is incorrect is line number: _______
Explain in one sentence how to change this line. Do not write code.
Answer: Line 5; We need to get
"shuffled" instead of data.
Recall a permutation test is simulating if samples come from the same
population. This means we need to shuffle the data and use it to see if
that would change our result/view. This means in line 5 we want to use
the shuffled data, so we need to do .get(“shuffled”)
instead of .get(“data”).
The average score on this problem was 50%.
The third line that is incorrect is line number: _______
Explain in one sentence how to change this line. Do not write code.
Answer: Line 8; Move it outside of the
for-loop (unindent).
If we have return inside of the for-loop it
will terminate after it goes through the code once! This means all we
have to do is unindent return, moving it outside of the
for-loop.
The average score on this problem was 67%.
Suppose you’ve fixed all the issues with this function, as you described above. Now, you want to use this corrected function to run a permutation test with the following hypotheses:
For this permutation test, consider a children’s game to be a game
that has "Children’s Games" as part of the
"Domains" column. A dice-rolling game is one that has
"Dice Rolling" as part of the "Mechanics"
column, and a non-dice-rolling game is one that does not have
"Dice Rolling" as part of the "Mechanics"
column.
The DataFrame with_dice is defined as follows.
with_dice = games.assign(isDice = games.get("Mechanics").str.contains("Dice Rolling"))Write one line of code that creates an array called
simulated_diffs containing 1000 simulated differences in
group means for this permutation test. You should call your
perm_test function here!
Answer:
simulated diffs = perm_test(with dice[with dice.get("Domains").str.contains("Children’s Games")], "isDice", "Play Time")The inputs to perm_test, in order, are:
Here, the only relevant information is information on
"Children's Games", so the first argument to
perm_test must be a DataFrame in which the
"Domains" column contains "Children's Games",
as described in the question.
Then, since we’re testing whether the distribution of
"Play Time" is different for dice games and non-dice games,
we know that the column with group labels is "isDice"
(which is defined in the call to .assign that is provided
to us in the question), and the column with numerical information is
"Play Time".
The average score on this problem was 60%.
Suppose we’ve stored the observed value of the test statistic for
this permutation test in the variable obs_diff. Fill in the
blank below to find the p-value for this permutation test.
<
<=
>
>=
Answer: >=
We want to find if the simulated_diffs are more or as
extreme as the obs_diff. To be as or more extreme that
means it needs an equal sign. The other part of this is it cannot be
smaller because then it is not as extreme, which means
the answer must be >=.
The average score on this problem was 57%.
It’s your first time playing a new game called Brunch Menu. The deck contains 96 cards, and each player will be dealt a hand of 9 cards. The goal of the game is to avoid having certain cards, called Rotten Egg cards, which come with a penalty at the end of the game. But you’re not sure how many of the 96 cards in the game are Rotten Egg cards. So you decide to use the Central Limit Theorem to estimate the proportion of Rotten Egg cards in the deck based on the 9 random cards you are dealt in your hand.
You are dealt 3 Rotten Egg cards in your hand of 9 cards. You then construct a CLT-based 95% confidence interval for the proportion of Rotten Egg cards in the deck based on this sample. Approximately, how wide is your confidence interval?
Choose the closest answer, and use the following facts:
The standard deviation of a collection of 0s and 1s is \sqrt{(\text{Prop. of 0s}) \cdot (\text{Prop of 1s})}.
\sqrt{18} is about \frac{17}{4}.
\frac{17}{9}
\frac{17}{27}
\frac{17}{81}
\frac{17}{96}
Answer: \frac{17}{27}
A Central Limit Theorem-based 95% confidence interval for a population proportion is given by the following:
\left[ \text{Sample Proportion} - 2 \cdot \frac{\text{Sample SD}}{\sqrt{\text{Sample Size}}}, \text{Sample Proportion} + 2 \cdot \frac{\text{Sample SD}}{\sqrt{\text{Sample Size}}} \right]
Note that this interval uses the fact that (about) 95% of values in a normal distribution are within 2 standard deviations of the mean. It’s key to divide by \sqrt{\text{Sample Size}} when computing the standard deviation because the distribution that is roughly normal is the distribution of the sample mean (and hence, sample proportion), not the distribution of the sample itself.
The width of the above interval – that is, the right endpoint minus the left endpoint – is
\text{width} = 4 \cdot \frac{\text{Sample SD}}{\sqrt{\text{Sample Size}}}
From the provided hint, we have that
\text{Sample SD} = \sqrt{(\text{Prop. of 0s}) \cdot (\text{Prop of 1s})} = \sqrt{\frac{3}{9} \cdot \frac{6}{9}} = \frac{\sqrt{18}}{9}
Then, since we know that the sample size is 9 and that \sqrt{18} is about \frac{17}{4}, we have
\text{width} = 4 \cdot \frac{\text{Sample SD}}{\sqrt{\text{Sample Size}}} = 4 \cdot \frac{\frac{\sqrt{18}}{9}}{\sqrt{9}} = 4 \cdot \frac{\sqrt{18}}{9 \cdot 3} = 4 \cdot \frac{\frac{17}{4}}{27} = \frac{17}{27}
The average score on this problem was 51%.
Which of the following are limitations of trying to use the Central Limit Theorem for this particular application? Select all that apply.
The CLT is for large random samples, and our sample was not very large.
The CLT is for random samples drawn with replacement, and our sample was drawn without replacement.
The CLT is for normally distributed data, and our data may not have been normally distributed.
The CLT is for sample means and sums, not sample proportions.
Answer: Options 1 and 2
Option 1: We use Central Limit Theorem (CLT) for large random samples, and a sample of 9 is considered to be very small. This makes it difficult to use CLT for this problem.
Option 2: Recall CLT happens when our sample is drawn with replacement. When we are handed nine cards we are never replacing cards back into our deck, which means that we are sampling without replacement.
Option 3: This is wrong because CLT states that a large sample is approximately a normal distribution even if the data itself is not normally distributed. This means it doesn’t matter if our data had not been normally distributed if we had a large enough sample we could use CLT.
Option 4: This is wrong because CLT does apply to the sample proportion distribution. Recall that proportions can be treated like means.
The average score on this problem was 77%.
In recent years, there has been an explosion of board games that teach computer programming skills, including CoderMindz, Robot Turtles, and Code Monkey Island. Many such games were made possible by Kickstarter crowdfunding campaigns.
Suppose that in one such game, players must prove their understanding
of functions and conditional statements by answering questions about the
function wham, defined below. Like players of this game,
you’ll also need to answer questions about this function.
1 def wham(a, b):
2 if a < b:
3 return a + 2
4 if a + 2 == b:
5 print(a + 3)
6 return b + 1
7 elif a - 1 > b:
8 print(a)
9 return a + 2
10 else:
11 return a + 1What is printed when we run print(wham(6, 4))?
Answer: 6 8
When we call wham(6, 4), a gets assigned to
the number 6 and b gets assigned to the number 4. In the
function we look at the first if-statement. The
if-statement is checking if a, 6, is less than
b, 4. We know 6 is not less than 4, so we skip this section
of code. Next we see the second if-statement which checks
if a, 6, plus 2 equals b, 4. We know 6 + 2 = 8, which is not equal to 4. We then
look at the elif-statement which asks if a, 6,
minus 1 is greater than b, 4. This is True! 6 - 1 = 5 and 5 > 4. So we
print(a), which will spit out 6 and then we will
return a + 2. a + 2 is 6 + 2. This means the function
wham will print 6 and return 8.
The average score on this problem was 81%.
Give an example of a pair of integers a and
b such that wham(a, b) returns
a + 1.
Answer: Any pair of integers a,
b with a = b or with
a = b + 1
The desired output is a + 1. So we want to look at the
function wham and see which condition is necessary to get
the output a + 1. It turns out that this can be found in
the else-block, which means we need to find an
a and b that will not satisfy any of the
if or elif-statements.
If a = b, so for example a points to 4 and
b points to 4 then: a is not less than
b (4 < 4), a + 2 is not equal to
b (4 + 2 = 6 and 6 does
not equal 4), and a - 1 is not greater than b
(4 - 1= 3) and 3 is not greater than
4.
If a = b + 1 this means that a is greater
than b, so for example if b is 4 then
a is 5 (4 + 1 = 5). If we
look at the if-statements then a < b is not
true (5 is greater than 4), a + 2 == b is also not true
(5 + 2 = 7 and 7 does not equal 4), and
a - 1 > b is also not true (5
- 1 = 4 and 4 is equal not greater than 4). This means it will
trigger the else statement.
The average score on this problem was 94%.
Which of the following lines of code will never be executed, for any input?
3
6
9
11
Answer: 6
For this to happen: a + 2 == b then a must
be less than b by 2. However if a is less than
b it will trigger the first if-statement. This
means this second if-statement will never run, which means
that the return on line 6 never happens.
The average score on this problem was 79%.
In the game Spot It, players race to identify an object that appears on two different cards. Each card contains images of eight objects, and exactly one object is common to both cards.

Suppose the objects appearing on each card are stored in an array,
and our task is to find the object that appears on both cards. Complete
the function find_match that takes as input two arrays of 8
objects each, with one object in common, and returns the name of the
object in both arrays.
For example, suppose we have two arrays defined as follows.
objects1 = np.array(["dragon", "spider", "car", "water droplet", "spiderweb", "candle", "ice cube", "ladybug"])
objects2 = np.array(["zebra", "lock", "dinosaur", "eye", "fire", "shamrock", "spider", "carrot"])Then find_match(objects1, objects2) should evaluate to
"spider". Your function must include a for loop, and it
must take at most three lines of code (not counting the
line with def).
Answer:
def find_match(array1, array2):
for obj in array1:
if obj in array2:
return objWe first need to define the function find_match(). We
can gather since we are feeding in two groups of objects we are giving
find_match() two parameters, which we have called
array1 and array2. The next step is utilizing
a for-loop. We want to look at all the objects inside of
array1 and then check using an if-statement if
that object exists in array2. If it does, we can stop the
loop and return the object!
The average score on this problem was 67%.
Now suppose the objects appearing on each card are stored in a
DataFrame with 8 rows and one column called "object".
Complete the function find_match_again that takes as input
two such DataFrames with one object in common and returns the nameof the
object in both DataFrames.
Your function may not call the previous function
find_match, and it must take exactly one line of
code (not counting the line with def).
Answer:
def find_match_again(df1, df2)
return df1.merge(df2, on = “object”).get(“object”).iloc[0]Once again we need to define our function and then have two
parameters for the two DataFrames. Recall the method
.merge() which will combine two DataFrames and only give us
the elements that are shared. The directions tell us that both
DataFrames have a single column called “object”. Since we
want to combine the DataFrames on that column we do have:
df1.merge(df2, on = “object”). Once we have merged the
DataFrames we should have only 1 row with the index and the column
“object”. To isolate the element inside of this DataFrame
we can first get a Series by doing .get(“object”) and then
do .iloc[0] to get the element inside of the Series.
The average score on this problem was 46%.
Dylan, Harshi, and Selim are playing a variant of a dice game called Left, Center, Right (LCR) in which there are 9 chips (tokens) and 9 dice. Each player starts off with 3 chips. Each die has the following six sides: L, C, R, Dot, Dot, Dot.
During a given player’s turn, they must roll a number of dice equal to the number of chips they currently have. Each die determines what to do with one chip:
Since the number of dice rolled is the same as the number of chips the player has, the dice rolls determine exactly what to do with each chip. There is no strategy at all in this simple game.
Dylan will take his turn first (we’ll call him Player 0), then at the end of his turn, he’ll pass the dice to his left and play will continue clockwise around the table. Harshi (Player 1) will go next, then Selim (Player 2), then back to Dylan, and so on.
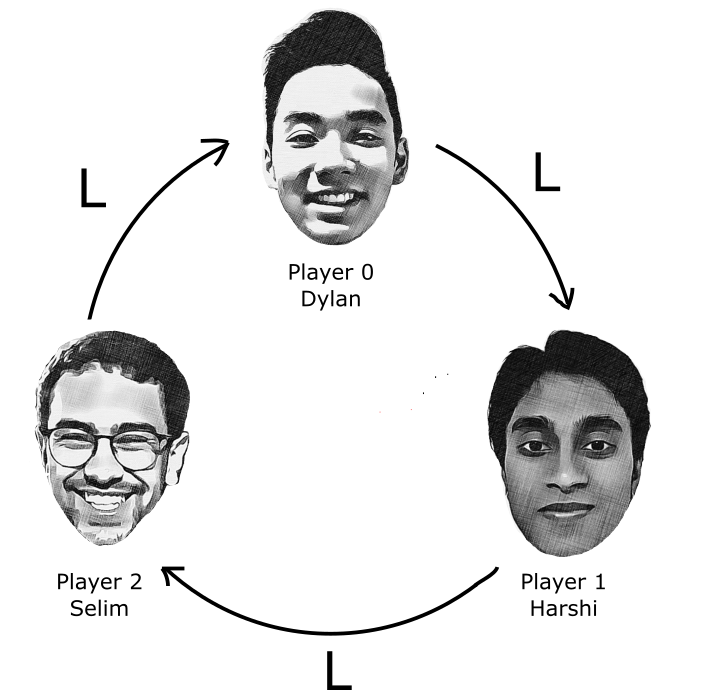
Note that if someone has no chips when it’s their turn, they are still in the game and they still take their turn, they just roll 0 dice because they have 0 chips. The game ends when only one person is holding chips, and that person is the winner. If 300 turns have been taken (100 turns each), the game will end and we’ll declare it a tie.
The function simulate_lcr below simulates one full game
of Left, Center, Right and returns the number of turns taken in
that game. Some parts of the code are not provided. You will need to
fill in the code for the parts marked with a blank. The parts marked
with ... are not provided, but you don’t need to fill them
in because they are very similar to other parts that you do need to
complete.
Hint: Recall that in Python, the % operator gives the remainder upon division. For example 12 % 5 is 2.
def simulate_lcr():
# stores the number of chips for players 0, 1, 2 (in that order)
player_chips = np.array([3,3,3])
# maximum of 300 turns allotted for the game
for i in np.arange(300):
# which player's turn it is currently (0, 1, or 2)
current_player = __(a)__
# stores what the player rolled on their turn
roll = np.random.choice(["L", "C", "R", "Dot", "Dot", "Dot"], __(b)__)
# count the number of instances of L, C, and R
L_count = __(c)__
C_count = ...
R_count = ...
if current_player == 0:
# update player_chips based on what player 0 rolled
player_chips = player_chips + np.array(__(d)__)
elif current_player == 1:
# update player_chips based on what player 1 rolled
player_chips = player_chips + ...
else:
# update player_chips based on what player 2 rolled
player_chips = player_chips + ...
# if the game is over, return the number of turns played
if __(e)__:
return __(f)__
# if no one wins after 300 turns, return 300
return 300What goes in blank (a)?
Answer: i % 3
We are trying to find which player’s turn it is within the
for-loop. We know that each player: Dylan, Harshi, and
Selim will play a maximum of 100 turns. Notice that the
for-loop goes from 0 to 299. This means we need to
manipulate the i somehow to figure out whose turn it is.
The hint here is extremely helpful. The maximum remainder we want to
have is 2 (recall the players are called Player 0, Player 1, and Player
2). This means we can utilize % to give us the remainder of
i / 3, which would tell us which player’s turn it is.
The average score on this problem was 41%.
What goes in blank (b)?
Answer:
player_chips[current_player]
Recall np.random.choice() must be given an array and can
then optionally be given a size to get multiple values
instead of one. We know that player_chips is an array of
the chips for each player. To access a specific player’s chips we can
use [current_player] because the 1st index of
player_chips corresponds to Player 0, the 2nd index
corresponds to Player 1, and the 3rd index corresponds to Player 2.
The average score on this problem was 51%.
What goes in blank (c)?
Answer: `np.count_nonzero(roll == “L”)
We know that if we do roll == “L” then we get an array
which changes the index of each element in roll to
True if that element equals “L” and
False otherwise. We can then use
np.count_nonzero() to count the number of True
values there are.
The average score on this problem was 61%.
What goes in blank (d)?
Answer:
[-(L_count + C_count + R_count), L_count, R_count]
Recall the rules of the games:
If we are Player 0 the person to our left is Player 1 and the person
to our right is Player 2. We want to update player_chips to
appropriately give the players to our left and right chips. This means
we can add our own array with the element at index 1 be our
L_count and the element at index 2 be our
R_count. We need to also subtract the tokens we are giving
away and C_count, so in index 0 we have:
-(L_count + C_count + R_count).
The average score on this problem was 51%.
What goes in blank (e)?
Answer:
np.count_nonzero(player_chips) == 1
We want to stop the game early if only one person has chips. To do
this we can use np.count_nonzero(player_chips) to count the
number of elements inside player_chips that have chips. If
the player does not have chips then their index would have 0 inside of
it.
The average score on this problem was 61%.
What goes in blank (f)?
Answer: i + 1
To find the number of turns played we simply need to add 1 to
i. We do this because i starts at 0!
The average score on this problem was 53%.
Suppose the function simulate_lcr from the last question
has been correctly implemented, and we want to use it to see how many
turns a game of Left, Center, Right usually takes.
Note: You can answer this question even if you couldn’t answer the previous one.
Consider the code and histogram below.
turns = np.array([])
for i in np.arange(10000):
turns = np.append(turns, simulate_lcr())
(bpd.DataFrame().assign(turns=turns).plot(kind="hist", density = True, ec="w", bins = np.arange(0, 66, 6)))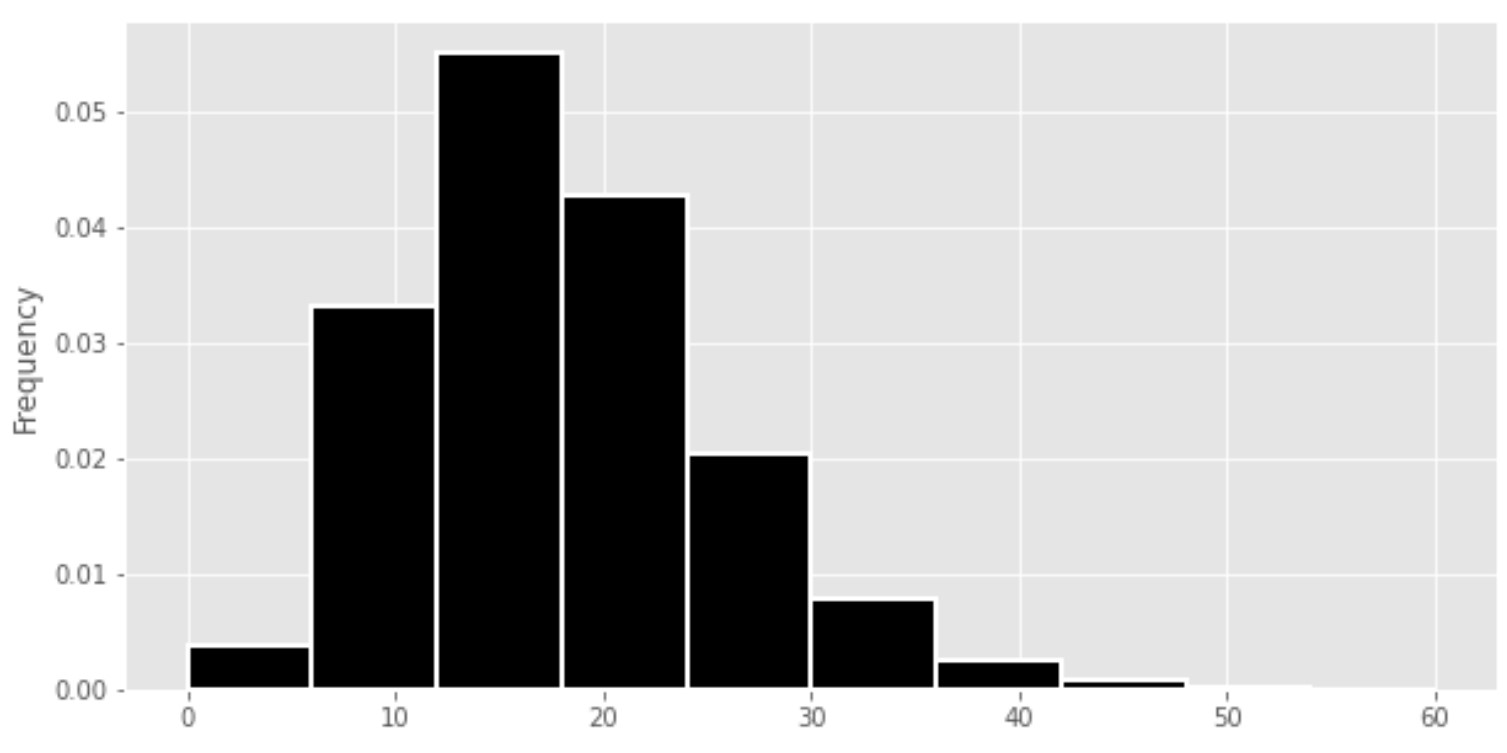
Does this histogram show a probability distribution or an empirical distribution?
Probability Distribution
Empirical Distribution
Answer: Empirical Distribution
An empirical distribution is derived from observed data, in this case, the results of 10,000 simulated games of Left, Center, Right. It represents the frequencies of outcomes (number of turns taken in each game) as observed in these simulations.
The average score on this problem was 54%.
What is the probability of a game of Left, Center, Right lasting 30 turns or more? Choose the closest answer below.
0.01
0.06
0.10
0.60
Answer: 0.06
We’re being asked to find the proportion of values in the histogram that are greater than or equal to 30, which is equal to the area of the histogram to the right of 30. Immediately, we can rule out 0.01 and 0.60, because the area to the right of 30 is more than 1% of the total area and less than 60% of the total area.
The problem then boils down to determining whether the area to the right of 30 is 0.06 or 0.10. While you could solve this by finding the areas of the three bars individually and adding them together, there’s a quicker solution. Notice that the x-axis gridlines – the vertical lines in the background in white – appear every 10 units (at x = 0, x = 10, x = 20, x = 30, and so on) and the y-axis gridlines – the horizontal lines in the background in white – appear every 0.01 units (at y = 0, y = 0.01, y = 0.02, and so on). There’s a “box” in the grid between x = 30 and x = 40, and between y = 0 and y = 0.01. The area of that box is (40 - 30) \cdot 0.01 = 0.1, which means that if a bar book up the entire box, then 10% of the values in this distribution would fall into that bar’s bin.
So, to decide whether the area to the right of 30 is closer to 0.06 or 0.1, we can estimate whether the three bars to the right of 30 would fill up the entire box described above (that is, the box from 30 to 40 on the x-axis and 0 to 0.1 on the y-axis), or whether it would be much emptier. Visually, if you broke off the area that is to the right of 40 in the histogram and put it in the box we’ve just described, then quite a bit of the box would still be empty. As such, the area to the right of 30 is less than the area of the box, so it’s less than 0.1, and so the only valid option is 0.06.
The average score on this problem was 50%.
Suppose a player with n chips takes their turn. What is the probability that they will have to put at least one chip into the center? Give your answer as a mathematical expression involving n.
Answer: 1 - (\frac{5}{6})^n
Recall that the die used to play this game has six sides: L, C, R, Dot, Dot, Dot. The chance of getting C is \frac{1}{6}. So we can take the compliment of that to get \frac{5}{6}, which is the probability of not putting at least one chip into the center and then doing (\frac{5}{6})^n. Once again we must use the complement rule as to convert it back to the probability of putting at least one chip into the center. This gives us the answer: 1 - (\frac{5}{6})^n
The average score on this problem was 56%.
Suppose a player with n chips takes their turn. What is the probability that they will end their turn with n chips? Give your answer as a mathematical expression involving n.
Answer: \left( \frac{1}{2} \right)^n
Recall, when it is a player’s turn, they roll one die for each of the n chips they have. The die that they roll has six faces. In three of those faces (L, C, and R), they end up losing a chip, and in the other three of those faces (dot, dot, and dot), they keep the chip. So, for each chip, there is a \frac{3}{6} = \frac{1}{2} chance that they get to keep it after the turn. Since each die roll is independent, there is a \frac{1}{2} \cdot \frac{1}{2} \cdot ... \cdot \frac{1}{2} = \left( \frac{1}{2} \right)^n chance that they get to keep all n chips. (Note that there is no way to earn more chips during a turn, so that’s not something we need to consider.)
The average score on this problem was 69%.
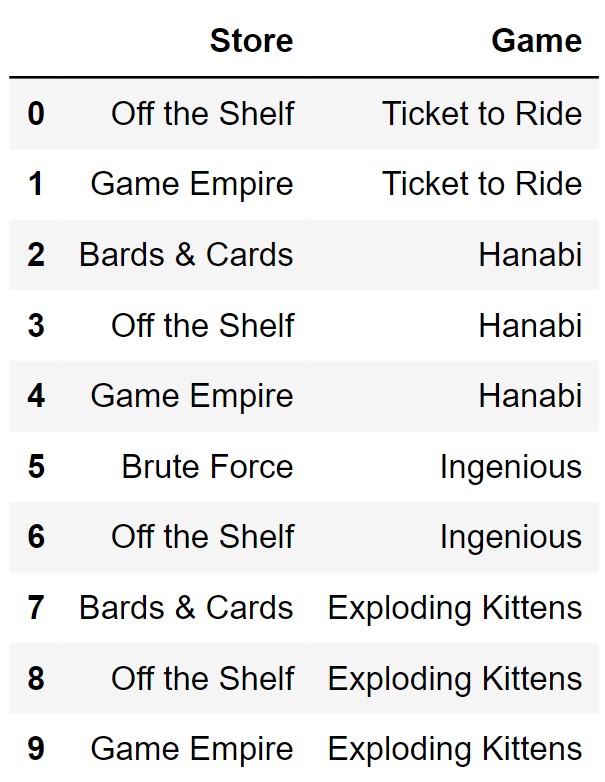
At a recent game night, you played several new board games and liked them so much that you now want to buy copies for yourself.
The DataFrame stores is shown below in full. Each row
represents a game you want to buy and a local board game store where
that game is available for purchase. If a game is not available at a
certain store, there will be no row corresponding to that store and that
game.
The DataFrame prices has five rows. Below we merge
stores with prices and display the output in
full.
merged = stores.merge(prices, on="Game")
merged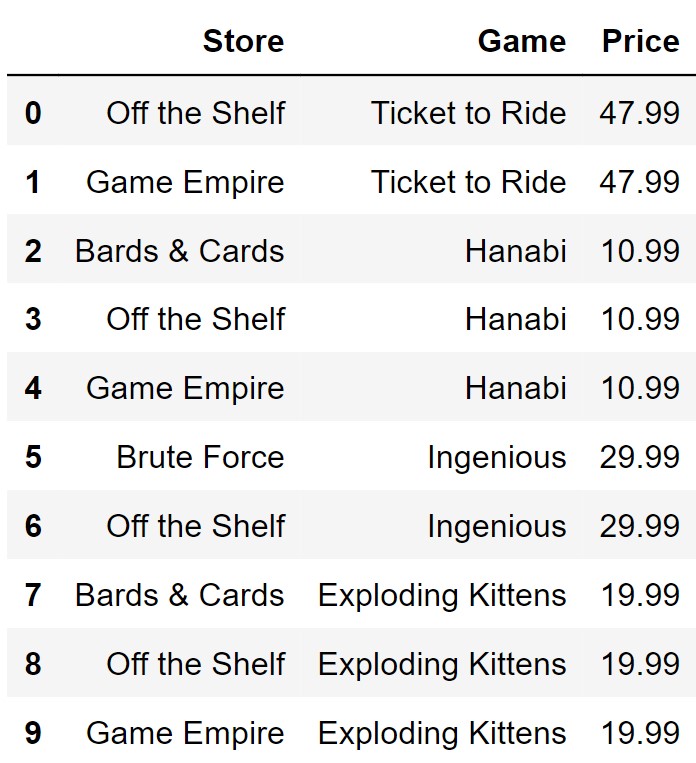
In the space below, specify what the DataFrame prices
could look like. The column labels should go in the top
row, and the row labels (index) should go in the leftmost row. You may
not need to use all the columns provided, but you are told that
prices has five rows, so you should use all rows
provided.
Note: There are several correct answers to this question.
Answer:
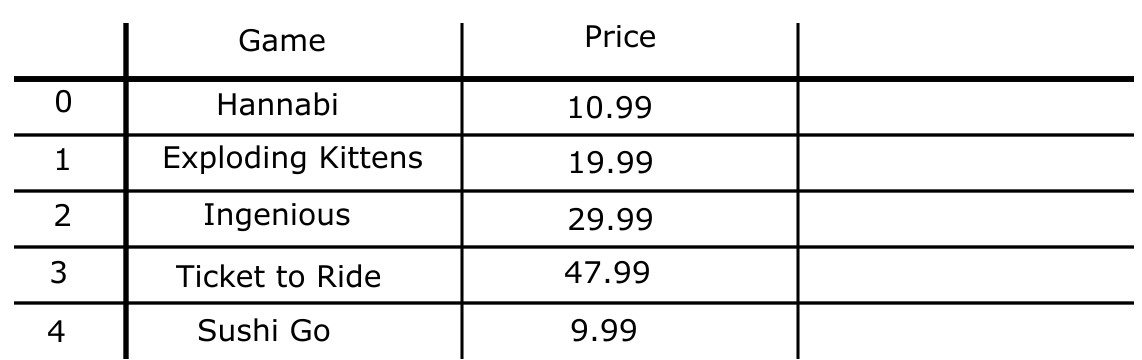
We can use the merged DataFrame to figure out the prices
that correlate to each game in stores. We see in
merged the price for Tickets to Ride should be
47.99, so we create a row for that game. We repeat this process to find
the remaining rows. Since we know that prices have 5 rows
we then make a game and price up. Note that in the solution above the
last row (index 4) has “Sushi Go” and 9.99.
These can be any game or any price that is not listed in indexes 0 to 4.
This is because prices has 5 rows and when we use
.merge() since the game “Sushi Go” is not in
stores it will not be added.
The average score on this problem was 84%.
Suppose merged now contains all the available games and
their corresponding prices at each store (in particular, a given game is
sold for the same price at all stores). You want to buy as many games as
possible but you only want to go to one store. Which store should you go
to maximize the number of games you can buy?
Fill in the blanks so that where_to_go evaluates to the
name of the store you should buy your games from.
where_to_go = (merged.groupby("Store").__(a)__.sort_values(by="Price", ascending=False).__(b)__)What goes in blank (a)?
min()
max()
count()
mean()
Answer: count()
The problem asks us which store would allow us to buy as many games
as possible. The provided code is
merge.groupby(“Store”).__a__. We want to use the aggregate
method that allows us to find the number of games in each store. The
aggregation method for this would be count().
The average score on this problem was 87%.
What goes in blank (b)?
Answer: index[0]
Recall groupby() will cause the unique values from the
column “Store” to be in the index. The remaining part of
the code sorts the DataFrame so that the store with the most games is at
the top. This means the row at index 0 has the store and most number of
games inside of the DataFrame. To grab the element at the 1st index we
simply do index[0].
The average score on this problem was 53%.
Suppose you go to the store where_to_go and buy one copy
of each of the available games that you enjoyed at game night. How much
money will you spend? Write one line of code that
evaluates to the answer, using the merged DataFrame and no
others.
Answer:
merged[merged.get(“Store”) == where_to_go].get(“Price”).sum()
We want to figure out how much money we would spend if we went to
where_to_go, which is the store where we can buy as many
games as possible. We can simply query the merged DataFrame to only
contain the rows where the store is equal to where_to_go.
We then can simply get the “Price” column and add all of
the values up by doing .sum() on the Series.
The average score on this problem was 74%.
We collect data on the play times of 100 games of Chutes and Ladders (sometimes known as Snakes and Ladders) and want to use this data to perform a hypothesis test.
Which of the following pairs of hypotheses can we test using this data?
Option 1: Null Hypothesis: In a random sample of Chutes and Ladders games, the average play time is 30 minutes. Alternative Hypothesis: In a random sample of Chutes and Ladders games, the average play time is not 30 minutes.
Option 2: Null Hypothesis: In a random sample of Chutes and Ladders games, the average play time is not 30 minutes. Alternative Hypothesis: In a random sample of Chutes and Ladders games, the average play time is 30 minutes
Option 3: Null Hypothesis: A game of Chutes and Ladders takes, on average, 30 minutes to play. Alternative Hypothesis: A game of Chutes and Ladders does not take, on average, 30 minutes to play.
Option 4: Null Hypothesis: A game of Chutes and Ladders does not take, on average, 30 minutes to play. Alternative Hypothesis: A game of Chutes and Ladders takes, on average, 30 minutes to play.
Option 1
Option 2
Option 3
Option 4
Answer: Option 3
Option 3: is the correct answer because the Null Hypothesis can be applicable to the real world, and thus simulated, and has the test statistic “equal” to our prediction of 30 minutes. The Alternative Hypothesis is also correctly different from the Null Hypothesis by saying the test statistic is “not equal” to our prediction of 30 minutes.
Option 1: We want the Null Hypothesis or Alternative Hypothesis to be applicable to the real world, which means that by having the start “In a random sample…” we are discrediting this in the real world.
Option 2: Like Option 1, we want the Null Hypothesis or Alternative Hypothesis to be applicable to the real world, which means that by having the start “In a random sample…” we are discrediting this in the real world.
Option 4: This answer is wrong because the Null
Hypothesis should be focused on figuring out the positive test
statistic, in this case average. In other words, let u be
the average time to play Chutes and Ladders and let
u<sub>0<\sub> be 30 minutes. The Null
Hypothesis should be u =
u<sub>0<\sub> and the Alternative Hypothesis
should be something different, in this case: u !=
u<sub>0<\sub>.
The average score on this problem was 65%.
We use our collected data to construct a 95% CLT-based confidence interval for the average play time of a game of Chutes and Ladders. This 95% confidence interval is [26.47, 28.47]. For the 100 games for which we collected data, what is the mean and standard deviation of the play times?
Answer: mean = 27.47 and SD = 5
One of the key properties of the normal distribution is that about 95% of values lie within 2 standard deviations of the mean. The Central Limit Theorem states that the distribution of the sample mean is roughly normal, which means that to create this CLT-based 95% confidence interval, we used the 2 standard deviations rule.
What we’re given, then, is the following:
\begin{align*} \text{Sample Mean} + 2 \cdot \text{SD of Distribution of Possible Sample Means} &= 28.47 \\ \text{Sample Mean} - 2 \cdot \text{SD of Distribution of Possible Sample Means} &= 26.47 \end{align*}
The sample mean is halfway between 26.47 and 28.47, which is 27.47. Substituting this into the first equation gives us
\begin{align*}27.47 + 2 \cdot \text{SD of Distribution of Possible Sample Means} &= 28.47\\2 \cdot \text{SD of Distribution of Possible Sample Means} &= 1 \\ \text{Distribution of Possible Sample Means} &= 0.5\end{align*}
It can be tempting to conclude that the sample standard deviation is 0.5, but it’s not – the SD of the sample mean’s distribution is 0.5. Remember, the SD of the sample mean’s distribution is given by the square root law:
\text{SD of Distribution of Possible Sample Means} = \frac{\text{Population SD}}{\sqrt{\text{Sample Size}}} \approx \frac{\text{Sample SD}}{\sqrt{\text{Sample Size}}}
We don’t know the population SD, so we’ve used the sample SD as an estimate. As such, we have that
\text{SD of Distribution of Possible Sample Means} = 0.5 = \frac{\text{Sample SD}}{\sqrt{\text{Sample Size}}} = \frac{\text{Sample SD}}{\sqrt{100}}
So, \text{Sample SD} = 0.5 \cdot \sqrt{100} = 0.5 \cdot 10 = 5.
The average score on this problem was 64%.
Does the CLT say that the distribution of play times of the 100 games is roughly normal?
Yes
No
Answer: No
The Central Limit Theorem states that the distribution of the sample mean or the sample sum is roughly normal. The distribution of play times is a sample of size 100 drawn from the population of play times; the Central Limit Theorem doesn’t say anything about a population or any one sample.
The average score on this problem was 45%.
Of the two hypotheses you selected in part (a), which one is better supported by the data?
Null Hypothesis
Alternative Hypothesis
Answer: Alternative Hypothesis
To test the null hypothesis, we check whether 30 is in the confidence interval we constructed. 30 is not between 26.47 and 28.47, so we reject the null hypothesis that the average play time is 30 minutes.
The average score on this problem was 87%.