← return to practice.dsc10.com
Instructor(s): Suraj Rampure, Janine Tiefenbruck
This exam was administered in-person. The exam was closed-notes, except students were provided a copy of the DSC 10 Reference Sheet. No calculators were allowed. Students had 50 minutes to take this exam.
Here’s a walkthrough video of some of the problems on the exam.
Clue is a murder mystery game where players use the process of elimination to figure out the details of a crime. The premise is that a murder was committed inside a large home, by one of 6 suspects, with one of 7 weapons, and in one of 9 rooms.
The game comes with 22 cards, one for each of the 6 suspects, 7 weapons, and 9 rooms. To set up the game, one suspect card, one weapon card, and one room card are chosen randomly, without being looked at, and placed aside in an envelope. The cards in the envelope represent the details of the murder: who did it, with what weapon, and in what room.
The remaining 19 cards are randomly shuffled and dealt out to the players (as equally as possible). Players then look at the cards they were dealt and can conclude that any cards they see were not involved in the murder. In the gameplay, players take turns moving around to different rooms of the house on the gameboard, which gives them opportunities to see cards in other players’ hands and further eliminate suspects, weapons, and rooms. The first player to narrow it down to one suspect, with one weapon, and in one room can make an accusation and win the game!
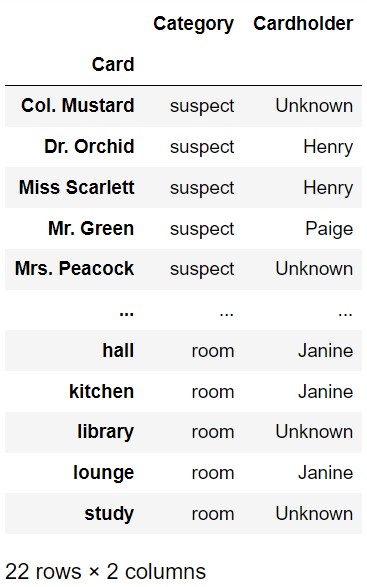
Suppose Janine, Henry, and Paige are playing a game of Clue. Janine
and Paige are each dealt 6 cards, and Henry is dealt 7. The DataFrame
clue has 22 rows, one for each card in the game.
clue represents Janine’s knowledge of who
is holding each card. clue is indexed by
“Card”, which contains the name of each suspect, weapon,
and room in the game. The “Category” column contains
“suspect”, “weapon”, or “room”.
The “Cardholder” column contains “Janine”,
“Henry”, “Paige”, or
“Unknown”.
Since Janine’s knowledge is changing throughout the game, the
“Cardholder” column needs to be updated frequently. At the
beginning of the game, the “Cardholder” column contains
only “Janine” and “Unknown” values. We’ll
assume throughout this exam that clue contains Janine’s
current knowledge at an arbitrary point in time, not necessarily at the
beginning of the game. For example, clue may look
like the DataFrame below.
Note: Throughout the exam, assume we have already
run import babypandas as bpd and
import numpy as np.
Each of the following expressions evaluates to an integer. Determine the value of that integer, if possible, or circle “not enough information."
Important: Before proceeding, make sure to read the page called Clue: The Murder Mystery Game.
(clue.get("Cardholder") == "Janine").sum() Answer: 6
This code counts the number of times that Janine appears in the
Cardholder column. This is because
clue.get("Cardholder") == "Janine" will return a Series of
True and False values of length 22 where
True corresponds to a card belonging to Janine. Since 6
cards were dealt to her, the expression evaluates to 6.
The average score on this problem was 78%.
np.count_nonzero(clue.get("Category").str.contains("p")) Answer: 13
This code counts the number of cells that contain that letter
"p" in the Category column.
clue.get("Category").str.contains("p") will return a Series
that contains True if "p" is part of the entry
in the "Category" column and False otherwise.
The words "suspect" and "weapons" both contain
the letter "p" and since there are 6 and 7 of each
respectively, the expression evaluates to 13.
The average score on this problem was 75%.
clue[(clue.get("Category") == "suspect") & (clue.get("Cardholder") == "Janine")].shape[0] Answer: not enough information
This code first filters only for rows that contain both
"suspect" as the category and "Janine" as the
cardholder and returns the number of rows of that DataFrame with
.shape[0]. However, from the information given, we do not
know how many "suspect" cards Janine has.
The average score on this problem was 83%.
len(clue.take(np.arange(5, 20, 3)).index) Answer: 5
np.arange(5, 20, 3) is the arary
np.array([5, 8, 11, 14, 17]). Recall that
.take will filter the DataFrame to contain only certain
rows, in this case rows 5, 8, 11, 14, and 17. Next, .index
extracts the index of the DataFrame, so the length of the index is the
same as the number of rows contained in the DataFrame. There are 5
rows.
The average score on this problem was 69%.
len(clue[clue.get("Category") >= "this"].index) Answer: 7
Similarly to the previous problem, we are getting the number of rows
of the DataFrame clue after filtering it.
clue.get("Category") >= "this" returns a Boolean Series
where True is returned when a string in "Category" is
greater than alphabetically than "this". This only happens
when the string is "weapon", which occurs 7 times.
The average score on this problem was 29%.
clue.groupby("Cardholder").count().get("Category").sum() Answer: 22
groupby("Cardholder").count() will return a DataFrame
indexed by "Cardholder" where each column contains the
number of cards that each "Cardholder" has. Then we sum the
values in the "Category" column, which evaluates to 22
because the sum of the total number of cards each cardholder has is the
total number of cards in play!
The average score on this problem was 52%.
Since Janine’s knowledge of who holds each card will change
throughout the game, the clue DataFrame needs to be updated
by setting particular entries.
Suppose more generally that we want to write a function that changes
the value of an entry in a DataFrame. The function should work for any
DataFrame, not just clue.
What parameters would such a function require? Say what each parameter represents.
Answer: We would need four parameters:
df, the DataFrame to change.
row, the row label or row number of the entry to
change.
col, the column label of the entry to
change.
val, the value that we want to store at that
location.
The average score on this problem was 43%.
An important part of the game is knowing when you’ve narrowed it down to just one suspect with one weapon in one room. Then you can make your accusation and win the game!
Suppose the DataFrames grouped and filtered
are defined as follows.
grouped = (clue.reset_index()
.groupby(["Category", "Cardholder"])
.count()
.reset_index())
filtered = grouped[grouped.get("Cardholder") == "Unknown"]Fill in the blank below so that "Ready to accuse" is
printed when Janine has enough information to make an accusation and win
the game.
if filtered.get("Card").______ == 3:
print("Ready to accuse")What goes in the blank?
count()
sum()
max()
min()
shape[0]
Answer: sum()
It is helpful to first visualize how both the grouped
(left) and filtered (right) DataFrames could look:
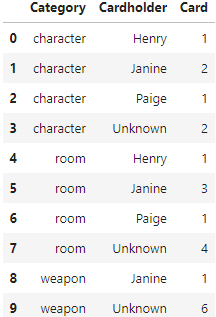
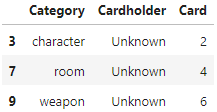
Now, let’s think about the scenario presented. We want a method that
will return 3 from filtered.get("Card").___. We do not use
count() because that is an aggregation function that
appears after a .groupby, and there is no grouping
here.
According to the instructions, we want to know when we narrowed it
down to just one suspect with one weapon in one room.
This means for filtered DataFrame, each row should have 1
in the "Card" column when you are already to accuse.
sum() works because when you have only 1 unknown card for
each of the three categories, that means you have a sum of 3 unknown
cards in total. You can make an accusation now!
The average score on this problem was 50%.
Now, let’s look at a different way to do the same thing. Fill in the
blank below so that "Ready to accuse" is printed when
Janine has enough information to make an accusation and win the
game.
if filtered.get("Card").______ == 1:
print("Ready to accuse")What goes in the blank?
count()
sum()
max()
min()
shape[0]
Answer: max()
This problem follows the same logic as the first except we only want
to accuse when filtered.get("Card").___ == 1. As we saw in
the previous part, we only want to accuse when all the numbers in the
"Card" column are 1, as this represents one unknown in each
category. This means the largest number in the "Card"
column must be 1, so we can fill in the blank with
max().
The average score on this problem was 40%.
When someone is ready to make an accusation, they make a statement such as:
“It was Miss Scarlett with the dagger in the study"
While the suspect, weapon, and room may be different, an accusation will always have this form:
“It was ______ with the ______ in the ______"
Suppose the array words is defined as follows (note the
spaces).
words = np.array(["It was ", " with the ", " in the "])Suppose another array called answers has been defined.
answers contains three elements: the name of the suspect,
weapon, and room that we would like to use in our accusation, in that
order. Using words and answers, complete the
for-loop below so that accusation is a string,
formatted as above, that represents our accusation.
accusation = ""
for i in ___(a)___:
accusation = ___(b)___What goes in blank (a)?
Answer: [0, 1, 2]
answers could potentially look like this array
np.array(['Mr. Green', 'knife', 'kitchen']). We want
accusation to be the following: “It was Mr. Green
with the knife in the kitchen” where the
underline represent the string from the words array and the
nonunderlined parts represent the string from the answers
array. In the for loop, we want to iterate through words and answers
simultaneously, so we can use [0, 1, 2] to represent the
indices of each array we will be iterating through.
The average score on this problem was 52%.
What goes in blank (b)?
Answer:
accusation + words[i] + answers[i]
We are performing string concatenation here. Using the example from
above, we want to add to the string accusation in order of
accusation, words, answer. After
all, we want “It was” before “Mr. Green”.
The average score on this problem was 56%.
Recall that the game Clue comes with 22 cards, one for each of the 6 suspects, 7 weapons, and 9 rooms. One suspect card, one weapon card, and one room card are chosen randomly, without being looked at, and placed aside in an envelope. The remaining 19 cards (5 suspects, 6 weapons, 8 rooms) are randomly shuffled and dealt out, splitting them as evenly as possible among the players. Suppose in a three-player game, Janine gets 6 cards, which are dealt one at a time.
Answer the probability questions that follow. Leave your answers unsimplified.
Cards are dealt one at a time. What is the probability that the first card Janine is dealt is a weapon card?
Answer: \frac{6}{19}
The probability of getting a weapon card is just the number of weapon cards divided by the total number of cards. There are 6 weapon cards and 19 cards total, so the probability has to be \frac{6}{19}. Note that it does not matter how the cards were dealt. Though each card is dealt one at a time to each player, Janine will always end up with a randomly selected 6 cards, out of the 19 cards available.
The average score on this problem was 80%.
What is the probability that all 6 of Janine’s cards are weapon cards?
Answer: \frac{6}{19} \cdot \frac{5}{18} \cdot \frac{4}{17} \cdot \frac{3}{16} \cdot \frac{2}{15} \cdot \frac{1}{14}
We can calculate the answer using the multiplication rule. The probability of getting Janine getting all the weapon cards is the probability of getting a dealt a weapon card first multiplied by the probability of getting a weapon card second multiplied by continuing probabilities of getting a weapon card until probability of getting a weapon card on the sixth draw. The denominator of each subsequent probability decreases by 1 because we remove one card from the total number of cards on each draw. The numerator also decreases by 1 because we remove a weapon card from the total number of available weapon cards on each draw.
The average score on this problem was 62%.
Determine the probability that exactly one of the first two cards Janine is dealt is a weapon card. This probability can be expressed in the form \frac{k \cdot (k + 1)}{m \cdot (m + 1)} where k and m are integers. What are the values of k and m?
Hint: There is no need for any sort of calculation that you can’t do easily in your head, such as long division or multiplication.
Answer: k = 12, m = 18
m has to be 18 because the denominator is the number of cards available during the first and second draw. We have 19 cards on the first draw and 18 on the second draw, so the only way to get that is for m = 18.
The probability that exactly one of the cards of your first two draws is a weapon card can be broken down into two cases: getting a weapon card first and then a non-weapon card, or getting a non-weapon card first and then a weapon card. We add the probabilities of the two cases together in order to calculate the overall probability, since the cases are mutually exclusive, meaning they cannot both happen at the same time.
Consider first the probability of getting a weapon card followed by a non-weapon card. This probability is \frac{6}{19} \cdot \frac{13}{18}. Similarly, the probability of getting a non-weapon card first, then a weapon card, is \frac{13}{19} \cdot \frac{6}{18}. The sum of these is \frac{6 \cdot 13}{19 \cdot 18} + \frac{13 \cdot 6}{19 \cdot 18}.
Since we want the numerator to look like k \cdot (k+1), we want to combine the terms in the numerator. Since the fractions in the sum are the same, we can represent the probability as 2 \cdot \frac{6}{19} \cdot \frac{13}{18}. Since 2\cdot 6 = 12, we can express the numerator as 12 \cdot 13, so k = 12.
The average score on this problem was 31%.
Which of the following probabilities could most easily be approximated by writing a simulation in Python? Select the best answer.
The probability that Janine wins the game.
The probability that a three-player game takes less than 30 minutes to play.
The probability that Janine has three or more suspect cards.
The probability that Janine visits the kitchen at some point in the game.
Answer: The probability that Janine has three or more suspect cards.
Let’s explain each choice and why it would be easy or difficult to simulate in Python. The first choice is difficult because these simulations depend on Janine’s strategies and decisions in the game. There is no way to simulate people’s choices. We can only simulate randomness. For the second choice, we are not given information on how long each part of the gameplay takes, so we would not be able to simulate the length of a game. The third choice is very plausible to do because when cards are dealt out to Janine, this is a random process which we can simulate in code, where we keep track of whether she has three of more suspect cards. The fourth choice follows the same reasoning as the first choice. There is no way to simulate Janine’s moves in the game, as it depends on the decisions she makes while playing.
The average score on this problem was 83%.
Part of the gameplay of Clue involves moving around the gameboard. The gameboard has 9 rooms, arranged on a grid, and players roll dice to determine how many spaces they can move.
The DataFrame dist contains a row and a column for each
of the 9 rooms. The entry in row r and
column c represents the shortest
distance between rooms r and c on the Clue gameboard, or the
smallest dice roll that would be required to move between rooms r and c.
Since you don’t need to move at all to get from a room to the same room,
the entries on the diagonal are all 0.
dist is indexed by "Room", and the room
names appear exactly as they appear in the index of the
clue DataFrame. These same values are also the column
labels in dist.
Two of the following expressions are equivalent, meaning they evaluate to the same value without erroring. Select these two expressions.
dist.get("kitchen").loc["library"]
dist.get("kitchen").iloc["library"]
dist.get("library").loc["kitchen"]
dist.get("library").iloc["kitchen"]
Explain in one sentence why these two expressions are the same.
Answer:
dist.get("kitchen").loc["library"] and
dist.get("library").loc["kitchen"]
dist.get("kitchen").iloc["library"] and
dist.get("library").iloc["kitchen"] are both wrong because
they uses iloc inappropriately. iloc[] takes
in an integer number representing the location of column, row, or cell
you would like to extract and it does not take a column or index
name.
dist.get("kitchen").loc["library"] and
dist.get("library").loc["kitchen"] lead to the same answer
because the DataFrame has a unique property! The entry at r, c is the
same as the entry at c, r because both are the distances for the same
two rooms. The distance from the kitchen to library is the same as the
distance from the library to kichen.
The average score on this problem was 84%.
On the Clue gameboard, there are two “secret passages." Each
secret passage connects two rooms. Players can immediately move through
secret passages without rolling, so in dist we record the
distance as 0 between two rooms that are connected with a secret
passage.
Suppose we run the following code.
nonzero = 0
for col in dist.columns:
nonzero = nonzero + np.count_nonzero(dist.get(col))Determine the value of nonzero after the above code is
run.
Answer: nonzero = 68
The nonzero variable represents the entries in the
DataFrame where the distance between two rooms is not 0. There are 81
entries in the DataFrame because there are 9 rooms and 9 \cdot 9 = 81. Since the diagonal of the
DataFrame is 0 (due to the distance from a room to itself being 0), we
know there are at most 72 = 81 - 9
nonzero entries in the DataFrame.
We are also told that there are 2 secret passages, each of which connects 2 different rooms, meaning the distance between these rooms is 0. Each secret passage will cause 2 entries in the DataFrame to have a distance of 0. For instance, if the secret passage was between the kitchen and dining room, then the distance from the kitchen to the dining room would be 0, but also the distance from the dining room to the kitchen would be 0. Since there are 2 secret passages and each gives rise to 2 entries that are 0, this is 4 additional entries that are 0. This means there are 68 nonzero entries in the DataFrame, coming from 81 - 9 - 4 = 68.
The average score on this problem was 28%.
Fill in blanks so that the expression below evaluates to a DataFrame
with all the same information as dist, plus one
extra column called "Cardholder" containing
Janine’s knowledge of who holds each room card.
dist.merge(___(a)___, ___(b)___, ___(c)___)What goes in blank (a)?
What goes in blank (b)?
What goes in blank (c)?
Answer:
clue.get(["Cardholder"])left_index=Trueright_index=TrueSince we want to create a DataFrame that looks like dist
with an extra column of "Cardholder", we want to extract
just that column from clue to merge with dist.
We do this with clue.get(["Cardholder"]). This is necessary
because when we merge two DataFrames, we get all columns from either
DataFrame in the end result.
When deciding what columns to merge on, we need to look for columns
from each DataFrame that share common values. In this case, the common
values in the two DataFrames are not in columns, but in the index, so we
use left_index=True and right_index=True.
The average score on this problem was 28%.
Suppose we generate a scatter plot as follows.
dist.plot(kind="scatter", x="kitchen", y="study");Suppose the scatterplot has a point at (4, 6). What can we conclude about the Clue gameboard?
The kitchen is 4 spaces away from the study.
The kitchen is 6 spaces away from the study.
Another room besides the kitchen is 4 spaces away from the study.
Another room besides the kitchen is 6 spaces away from the study.
Answer: Another room besides the kitchen is 6 spaces away from the study.
Let’s explain each choice and why it is correct or incorrect. The scatterplot shows how far a room is from the kitchen (as shown by values on the x-axis) and how far a room is from the study (as shown by the values on the y-axis). Each room is represented by a point. This means there is a room that is 4 units away from the kitchen and 6 units away from the study. This room can’t be the kitchen or study itself, since a room must be distance 0 from itself. Therefore, we conclude, based on the y-coordinate, that there is a room besides the kitchen that is 6 units away from the study.
The average score on this problem was 47%.
The histogram below shows the distribution of game times in minutes for both two-player and three-player games of Clue, with each distribution representing 1000 games played.
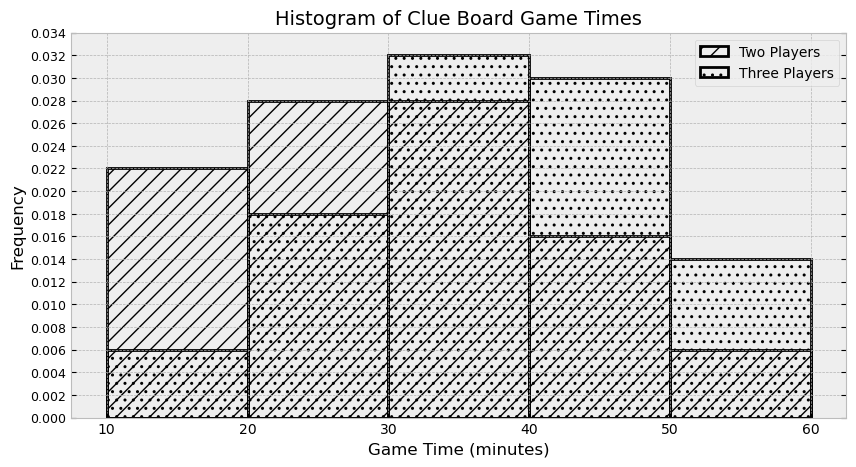
How many more three-player games than two-player games took at least 50 minutes to play? Give your answer as an integer, rounded to the nearest multiple of 10.
Answer: 80
First, calculate the number of three-player games that took at least 50 minutes. We can calculate this number by multiplying the area of that particular histogram bar (from 50 to 60) by the total number of three player games(1000 games) total. This results in (60-50) \cdot 0.014 \cdot 1000 = 140. We repeat the same process to find the number of two-player games that took at least 50 minutes, which is (60-50) \cdot 0.006 \cdot 1000 = 60. Then, we find the difference of these numbers, which is 140 - 60 = 80.
An easier way to calculate this is to measure the difference directly. We could do this by finding the area of the highlighted region below and then multiplying by the number of games. This represents the difference between the number of three-player games and the number of two player games. This, way we need to do just one calculation to get the same answer: (60 - 50) \cdot (0.014 - 0.006) \cdot 1000 = 80.
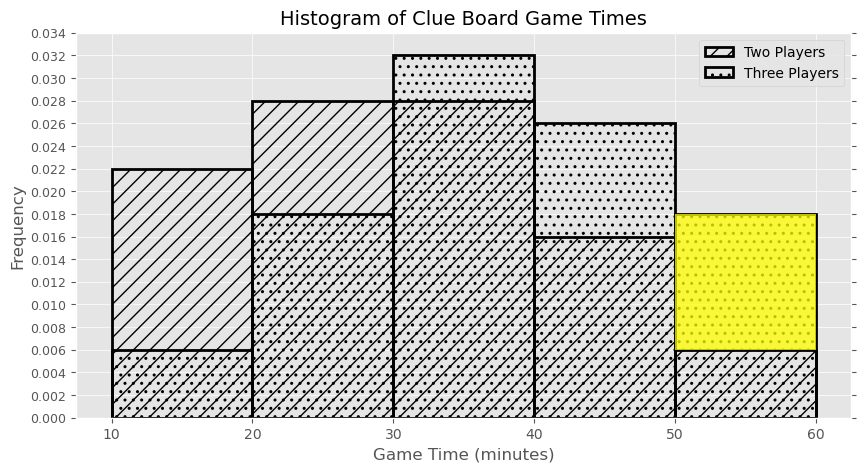
The average score on this problem was 61%.
Calculate the approximate area of overlap of the two histograms. Give your answer as a proportion between 0 and 1, rounded to two decimal places.
Answer: 0.74
To find the area of overlap of the two histograms, we can directly calculate the area of overlap in each bin and add them up as shown below. However, this requires a lot of calculation, and is not advised.
From 10-20: (20-10) \cdot 0.006 = 0.06
From 20-30: (30-20) \cdot 0.018 = 0.18
From 30-40: (40-30) \cdot 0.028 = 0.28
From 40-50: (50-40) \cdot 0.016 = 0.16
From 50-60: (60-50) \cdot 0.006 = 0.06
The summation of the overlap here is 0.74!
A much more efficient way to do this problem is to find the area of overlap by taking the total area of one distribution (which is 1) and subtracting the area in that distribution that does not overlap with the other. In the picture below, the only area in the two-player distribution that does not overlap with three-player distribution is highlighted. Notice there are only two regions to find the area of, so this is much easier. The calculation comes out the same: 1 - ((20 - 10) \cdot (0.022-0.006) + (30 - 20) \cdot (0.028 - 0.018) = 0.74.
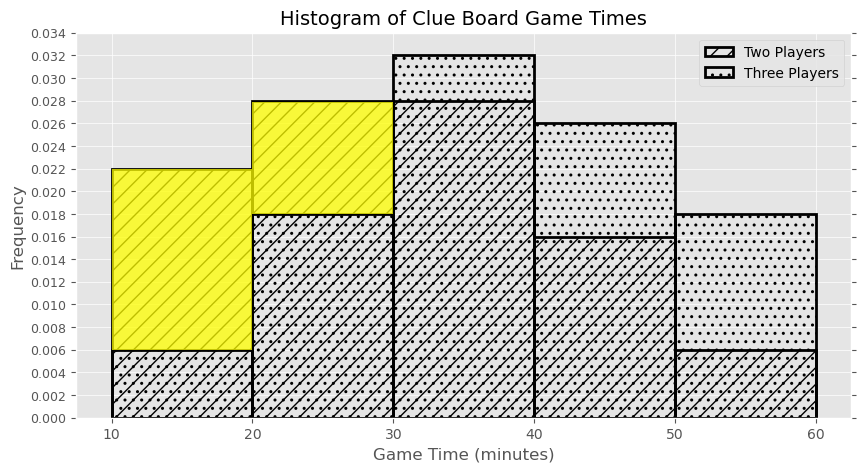
The average score on this problem was 56%.