← return to practice.dsc10.com

This quiz was administered in-person. It was closed-book and closed-note; students were not allowed to use the DSC 10 Reference Sheet. Students had 20 minutes to work on the quiz.

This quiz covered Lectures 21-24 of the Winter 2024 offering of DSC 10.

Note (groupby / pandas 2.0): Pandas 2.0+ no longer silently drops columns that can’t be aggregated after a groupby, so code written for older pandas may behave differently or raise errors. In these practice materials we use .get() to select the column(s) we want after .groupby(...).mean() (or other aggregations) so that our solutions run on current pandas. On real exams you will not be penalized for omitting .get() when the old behavior would have produced the same answer.

It can be hard to find a parking spot on UCSD’s campus! The parking DataFrame contains UCSD parking occupancy data for two on-campus parking structures. The "Structure" column contains either "Gilman" or "Hopkins". Each row of parking represents one day. The "Occupancy" column contains a float representing the proportion of occupied spaces at noon on that day. We’ll use this data to test the following hypotheses:

• Null Hypothesis: At noon, Gilman and Hopkins are equally occupied. The observed differences in our samples are simply due to random chance.

• Alternative Hypothesis: At noon, Hopkins is less occupied than Gilman. The observed differences in our samples cannot be explained by random chance alone.

As our test statistic, we will use the mean noontime "Occupancy" of Hopkins minus the mean noontime "Occupancy" of Gilman.

Problem 1

Problem 1.1

Suppose the Series s is defined as below. Write an expression involving s that evaluates to the observed value of the test statistic, and store the result in observed.

    s = parking.groupby("Structure").mean().get("Occupancy")
    observed = ______

What goes in the blank?

Problem 1.2

In running the permutation test, we need to do a simulation that runs many times, using a for-loop. What should be the first thing we do inside the for-loop?

• Initialize an empty array to store our results.

• Define a variable for the number of repetitions.

• Permute one of the columns of parking.

• Calculate the difference in group means.

Problem 1.3

Suppose we store 5000 simulated test statistics in the array differences. Choose the appropriate symbol to fill in the calculation of the p-value below.

p_value = np.count_nonzero(differences ______ observed) / 5000

• <

• <=

• ==

• !=

• >

• >=

Problem 1.4

Suppose the p-value of our test is 0.01 and we are testing the hypotheses at the 0.05 significance level. Which hypothesis is better supported by the data?

• Null

• Alternative

Problem 2

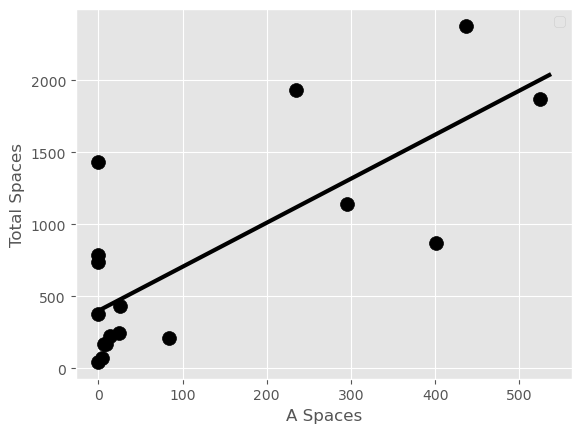
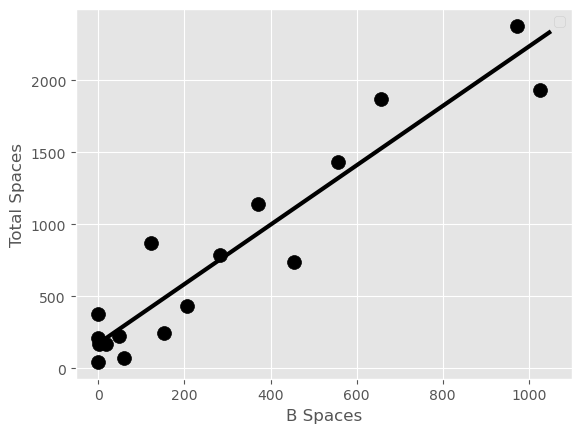
UCSD’s parking lots include A spaces for faculty, B spaces for staff, and S spaces for students.

The scatter plot on the left shows the relationship between the number of A spaces and the total number of parking spaces in each region of campus. Similarly, the scatter plot on the right shows the relationship between the number of B spaces and the total number of parking spaces in each region of campus. Note that these numbers represent a count of parking spaces existing on campus, and have nothing to do with occupancy.

Problem 2.1

Based on these scatter plots, which pair of variables has a larger correlation coefficient?

• A Spaces and Total Spaces

• B Spaces and Total Spaces

Problem 2.2

Which of the following variables would most likely be negatively associated with the total number of spaces in a campus region?

• Total area of the campus region

• Number of athletic fields in the campus region

• Number of residents in the campus region

• Number of electric vehicle charging stations in the campus region

Problem 2.3

The number of S spaces and the total number of parking spaces in each campus region are linearly related with a correlation coefficient of 0.6. The number of S spaces in the Warren College region of campus is 5 standard deviations below average. What does the regression line predict for the number of total spaces in Warren College, measured in standard units?

Problem 2.4

True or False: Since number of parking spaces is always a positive integer, the regression line that predicts the total number of spaces from the number of S spaces must have a positive y-intercept.

• True

• False

👋 Feedback: Find an error? Still confused? Have a suggestion? Let us know here.