
← return to practice.dsc10.com
Welcome! The problems shown below should be worked on on
paper, since the quizzes and exams you take in this course will
also be on paper. You do not need to submit your solutions anywhere.
We encourage you to complete this worksheet in groups during an
extra practice session on Friday, February 2nd. Solutions will be posted
after all sessions have finished. This problem set is not designed to
take any particular amount of time - focus on understanding concepts,
not on getting through all the questions.
Consider the function tom_nook, defined below. Recall
that if x is an integer, x % 2 is
0 if x is even and 1 if
x is odd.
def tom_nook(crossing):
bells = 0
for nook in np.arange(crossing):
if nook % 2 == 0:
bells = bells + 1
else:
bells = bells - 2
return bellsWhat value does tom_nook(8) evaluate to?
-6
-4
-2
0
2
4
6
Answer: -4
The average score on this problem was 79%.
The DataFrame evs consists of 32 rows, each of which
contains information about a different EV model.
The first few rows of evs are shown below.

We also have a DataFrame that contains the distribution of
“BodyStyle” for all “Brands” in evs, other than Nissan.
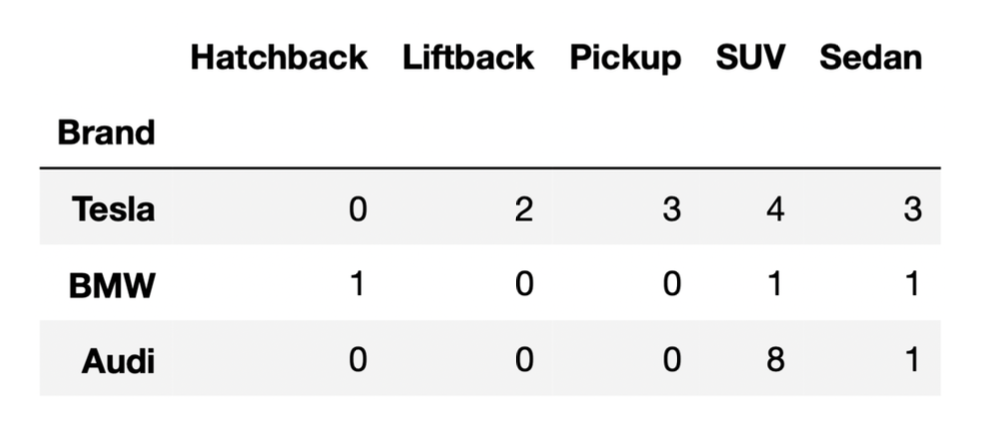
Suppose we’ve run the following few lines of code.
tesla = evs[evs.get("Brand") == "Tesla"]
bmw = evs[evs.get("Brand") == "BMW"]
audi = evs[evs.get("Brand") == "Audi"]
combo = tesla.merge(bmw, on="BodyStyle").merge(audi, on="BodyStyle")How many rows does the DataFrame combo have?
21
24
35
65
72
96
Answer: 35
Let’s attempt this problem step-by-step. We’ll first determine the
number of rows in tesla.merge(bmw, on="BodyStyle"), and
then determine the number of rows in combo. For the
purposes of the solution, let’s use temp to refer to the
first merged DataFrame,
tesla.merge(bmw, on="BodyStyle").
Recall, when we merge two DataFrames, the resulting
DataFrame contains a single row for every match between the two columns,
and rows in either DataFrame without a match disappear. In this problem,
the column that we’re looking for matches in is
"BodyStyle".
To determine the number of rows of temp, we need to
determine which rows of tesla have a
"BodyStyle" that matches a row in bmw. From
the DataFrame provided, we can see that the only
"BodyStyle"s in both tesla and
bmw are SUV and sedan. When we merge tesla and
bmw on "BodyStyle":
tesla each match the 1 SUV row in
bmw. This will create 4 SUV rows in temp.tesla each match the 1 sedan row in
bmw. This will create 3 sedan rows in
temp.So, temp is a DataFrame with a total of 7 rows, with 4
rows for SUVs and 3 rows for sedans (in the "BodyStyle")
column. Now, when we merge temp and audi on
"BodyStyle":
temp each match the 8 SUV rows in
audi. This will create 4 \cdot 8
= 32 SUV rows in combo.temp each match the 1 sedan row in
audi. This will create 3 \cdot 1
= 3 sedan rows in combo.Thus, the total number of rows in combo is 32 + 3 = 35.
Note: You may notice that 35 is the result of multiplying the
"SUV" and "Sedan" columns in the DataFrame
provided, and adding up the results. This problem is similar to Problem 5 from the Fall 2021
Midterm.
The average score on this problem was 45%.
The sums function takes in an array of numbers and
outputs the cumulative sum for each item in the array. The cumulative
sum for an element is the current element plus the sum of all the
previous elements in the array.
For example:
>>> sums(np.array([1, 2, 3, 4, 5]))
array([1, 3, 6, 10, 15])
>>> sums(np.array([100, 1, 1]))
array([100, 101, 102])The incomplete definition of sums is shown below.
def sums(arr):
res = _________
(a)
res = np.append(res, arr[0])
for i in _________:
(b)
res = np.append(res, _________)
(c)
return resFill in blank (a).
Answer: np.array([]) or
[]
res is the list in which we’ll be storing each
cumulative sum. Thus we start by initializing res to an
empty array or list.
The average score on this problem was 100%.
Fill in blank (b).
Answer: range(1, len(arr)) or
np.arange(1, len(arr))
We’re trying to loop through the indices of arr and
calculate the cumulative sum corresponding to each entry. To access each
index in sequential order, we simply use range() or
np.arange(). However, notice that we have already appended
the first entry of arr to res on line 3 of the
code snippet. (Note that the first entry of arr is the same
as the first cumulative sum.) Thus the lower bound of
range() (or np.arange()) actually starts at 1,
not 0. The upper bound is still len(arr) as usual.
The average score on this problem was 64%.
Fill in blank (c).
Answer: res[i - 1] + arr[i] or
sum(arr[:i + 1])
Looking at the syntax of the problem, the blank we have to fill
essentially requires us to calculate the current cumulative sum, since
the rest of line will already append the blank to res for
us. One way to think of a cumulative sum is to add the “current”
arr element to the previous cumulative sum, since the
previous cumulative sum encapsulates all the previous elements. Because
we have access to both of those values, we can easily represent it as
res[i - 1] + arr[i]. The second answer is more a more
direct approach. Because the cumulative sum is just the sum of all the
previous elements up to the current element, we can directly compute it
with sum(arr[:i + 1])
The average score on this problem was 71%.
True or False: If you roll two dice, the probability of rolling two fives is the same as the probability of rolling a six and a three.
Answer: False
The probability of rolling two fives can be found with 1/6 * 1/6 = 1/36. The probability of rolling a six and a three can be found with 2/6 (can roll either a 3 or 6) * 1/6 (roll a different side form 3 or 6, depending on what you rolled first) = 1/18. Therefore, the probabilities are not the same.
The average score on this problem was 33%.
Teresa and Sophia are bored while waiting in line at Bistro and decide to start flipping a UCSD-themed coin, with a picture of King Triton’s face as the heads side and a picture of his mermaid-like tail as the tails side.

Teresa flips the coin 21 times and sees 13 heads and 8 tails. She
stores this information in a DataFrame named teresa that
has 21 rows and 2 columns, such that:
The "flips" column contains "Heads" 13
times and "Tails" 8 times.
The "Wolftown" column contains "Teresa"
21 times.
Then, Sophia flips the coin 11 times and sees 4 heads and 7 tails.
She stores this information in a DataFrame named sophia
that has 11 rows and 2 columns, such that:
The "flips" column contains "Heads" 4
times and "Tails" 7 times.
The "Makai" column contains "Sophia" 11
times.
How many rows are in the following DataFrame? Give your answer as an integer.
teresa.merge(sophia, on="flips")Hint: The answer is less than 200.
Answer: 108
Since we used the argument on="flips, rows from
teresa and sophia will be combined whenever
they have matching values in their "flips" columns.
For the teresa DataFrame:
"Heads" in the
"flips" column."Tails" in the
"flips" column.For the sophia DataFrame:
"Heads" in the
"flips" column."Tails" in the
"flips" column.The merged DataFrame will also only have the values
"Heads" and "Tails" in its
"flips" column. - The 13 "Heads" rows from
teresa will each pair with the 4 "Heads" rows
from sophia. This results in 13
\cdot 4 = 52 rows with "Heads" - The 8
"Tails" rows from teresa will each pair with
the 7 "Tails" rows from sophia. This results
in 8 \cdot 7 = 56 rows with
"Tails".
Then, the total number of rows in the merged DataFrame is 52 + 56 = 108.
The average score on this problem was 54%.
Let A be your answer to the previous part. Now, suppose that:
teresa contains an additional row, whose
"flips" value is "Total" and whose
"Wolftown" value is 21.
sophia contains an additional row, whose
"flips" value is "Total" and whose
"Makai" value is 11.
Suppose we again merge teresa and sophia on
the "flips" column. In terms of A, how many rows are in the new merged
DataFrame?
A
A+1
A+2
A+4
A+231
Answer: A+1
The additional row in each DataFrame has a unique
"flips" value of "Total". When we merge on the
"flips" column, this unique value will only create a single
new row in the merged DataFrame, as it pairs the "Total"
from teresa with the "Total" from
sophia. The rest of the rows are the same as in the
previous merge, and as such, they will contribute the same number of
rows, A, to the merged DataFrame. Thus,
the total number of rows in the new merged DataFrame will be A (from the original matching rows) plus 1
(from the new "Total" rows), which sums up to A+1.
The average score on this problem was 46%.
The HAUGA bedroom furniture set includes two items, a bed frame and a bedside table. Suppose the amount of time it takes someone to assemble the bed frame is a random quantity drawn from the probability distribution below.
| Time to assemble bed frame | Probability |
|---|---|
| 10 minutes | 0.1 |
| 20 minutes | 0.4 |
| 30 minutes | 0.5 |
Similarly, the time it takes someone to assemble the bedside table is a random quantity, independent of the time it takes them to assemble the bed frame, drawn from the probability distribution below.
| Time to assemble bedside table | Probability |
|---|---|
| 30 minutes | 0.3 |
| 40 minutes | 0.4 |
| 50 minutes | 0.3 |
What is the probability that Stella assembles the bed frame in 10 minutes if we know it took her less than 30 minutes to assemble? Give your answer as a decimal between 0 and 1.
Answer: 0.2
We want to find the probability that Stella assembles the bed frame in 10 minutes, given that she assembles it in less than 30 minutes. The multiplication rule can be rearranged to find the conditional probability of one event given another.
\begin{aligned} P(A \text{ and } B) &= P(A \text{ given } B)*P(B)\\ P(A \text{ given } B) &= \frac{P(A \text{ and } B)}{P(B)} \end{aligned}
Let’s, therefore, define events A and B as follows:
Since 10 minutes is less than 30 minutes, A \text{ and } B is the same as A in this case. Therefore, P(A \text{ and } B) = P(A) = 0.1.
Since there are only two ways to complete the bed frame in less than 30 minutes (10 minutes or 20 minutes), it is straightforward to find P(B) using the addition rule P(B) = 0.1 + 0.4. The addition rule can be used here because assembling the bed frame in 10 minutes and assembling the bed frame in 20 minutes are mutually exclusive. We could alternatively find P(B) using the complement rule, since the only way not to complete the bed frame in less than 30 minutes is to complete it in exactly 30 minutes, which happens with a probability of 0.5. We’d get the same answer, P(B) = 1 - 0.5 = 0.5.
Plugging these numbers in gives our answer.
\begin{aligned} P(A \text{ given } B) &= \frac{P(A \text{ and } B)}{P(B)}\\ &= \frac{0.1}{0.5}\\ &= 0.2 \end{aligned}
The average score on this problem was 72%.
What is the probability that Ryland assembles the bedside table in 40 minutes if we know that it took him 30 minutes to assemble the bed frame? Give your answer as a decimal between 0 and 1
Answer: 0.4
We are told that the time it takes someone to assemble the bedside table is a random quantity, independent of the time it takes them to assemble the bed frame. Therefore we can disregard the information about the time it took him to assemble the bed frame and read directly from the probability distribution that his probability of assembling the bedside table in 40 minutes is 0.4.
The average score on this problem was 82%.
What is the probability that Jin assembles the complete HAUGA set in at most 60 minutes? Give your answer as a decimal between 0 and 1.
Answer: 0.53
There are several different ways for the total assembly time to take at most 60 minutes:
Using the multiplication rule, these probabilities are:
Finally, adding them up because they represent mutually exclusive cases, we get 0.1+0.28+0.15 = 0.53.
The average score on this problem was 58%.
In recent years, there has been an explosion of board games that teach computer programming skills, including CoderMindz, Robot Turtles, and Code Monkey Island. Many such games were made possible by Kickstarter crowdfunding campaigns.
Suppose that in one such game, players must prove their understanding
of functions and conditional statements by answering questions about the
function wham, defined below. Like players of this game,
you’ll also need to answer questions about this function.
1 def wham(a, b):
2 if a < b:
3 return a + 2
4 if a + 2 == b:
5 print(a + 3)
6 return b + 1
7 elif a - 1 > b:
8 print(a)
9 return a + 2
10 else:
11 return a + 1What is printed when we run print(wham(6, 4))?
Answer: 6 8
When we call wham(6, 4), a gets assigned to
the number 6 and b gets assigned to the number 4. In the
function we look at the first if-statement. The
if-statement is checking if a, 6, is less than
b, 4. We know 6 is not less than 4, so we skip this section
of code. Next we see the second if-statement which checks
if a, 6, plus 2 equals b, 4. We know 6 + 2 = 8, which is not equal to 4. We then
look at the elif-statement which asks if a, 6,
minus 1 is greater than b, 4. This is True! 6 - 1 = 5 and 5 > 4. So we
print(a), which will spit out 6 and then we will
return a + 2. a + 2 is 6 + 2. This means the function
wham will print 6 and return 8.
The average score on this problem was 81%.
Give an example of a pair of integers a and
b such that wham(a, b) returns
a + 1.
Answer: Any pair of integers a,
b with a = b or with
a = b + 1
The desired output is a + 1. So we want to look at the
function wham and see which condition is necessary to get
the output a + 1. It turns out that this can be found in
the else-block, which means we need to find an
a and b that will not satisfy any of the
if or elif-statements.
If a = b, so for example a points to 4 and
b points to 4 then: a is not less than
b (4 < 4), a + 2 is not equal to
b (4 + 2 = 6 and 6 does
not equal 4), and a - 1 is not greater than b
(4 - 1= 3) and 3 is not greater than
4.
If a = b + 1 this means that a is greater
than b, so for example if b is 4 then
a is 5 (4 + 1 = 5). If we
look at the if-statements then a < b is not
true (5 is greater than 4), a + 2 == b is also not true
(5 + 2 = 7 and 7 does not equal 4), and
a - 1 > b is also not true (5
- 1 = 4 and 4 is equal not greater than 4). This means it will
trigger the else statement.
The average score on this problem was 94%.
Which of the following lines of code will never be executed, for any input?
3
6
9
11
Answer: 6
For this to happen: a + 2 == b then a must
be less than b by 2. However if a is less than
b it will trigger the first if-statement. This
means this second if-statement will never run, which means
that the return on line 6 never happens.
The average score on this problem was 79%.
King Triton had four children, and each of his four children started their own families. These four families organize a Triton family reunion each year. The compositions of the four families are as follows:
Family W: "1a4c"
Family X: "2a1c"
Family Y: "2a3c"
Family Z: "1a1c"
Suppose we choose one of the fifteen people at the Triton family reunion at random.
Given that the chosen individual is from a family with one child, what is the probability that they are from Family X? Give your answer as a simplified fraction.
Answer: \frac{3}{5}
Given that the chosen individual is from a family with one child, we know that they must be from either Family X or Family Z. There are three individuals in Family X, and there are a total of five individuals from these two families. Thus, the probability of choosing any one of the three individuals from Family X out of the five individuals from both families is \frac{3}{5}.
The average score on this problem was 43%.
Consider the events A and B, defined below.
A: The chosen individual is an adult.
B: The chosen individual is a child.
True or False: Events A and B are independent.
True
False
Answer: False
If two events are independent, knowledge of one event happening does not change the probability of the other event happening. In this case, events A and B are not independent because knowledge of one event gives complete knowledge of the other.
To see this, note that the probability of choosing a child randomly out of the fifteen individuals is \frac{9}{15}. That is, P(B) = \frac{9}{15}.
Suppose now that we know that the chosen individual is an adult. In this case, the probability that the chosen individual is a child is 0, because nobody is both a child and an adult. That is, P(B \text{ given } A) = 0, which is not the same as P(B) = \frac{9}{15}.
This problem illustrates the difference between mutually exclusive events and independent events. In this case A and B are mutually exclusive, because they cannot both happen. But that forces them to be dependent events, because knowing that someone is an adult completely determines the probability that they are a child (it’s zero!)
The average score on this problem was 33%.
Consider the events C and D, defined below.
C: The chosen individual is a child.
D: The chosen individual is from family Y.
True or False: Events C and D are independent.
True
False
Answer: True
If two events are independent, the probability of one event happening does not change when we know that the other event happens. In this case, events C and D are indeed independent.
If we know that the chosen individual is a child, the probability that they come from Family Y is \frac{3}{9}, which simplifies to \frac{1}{3}. That is P(D \text{ given } C) = \frac{1}{3}.
On the other hand, without any prior knowledge, when we select someone randomly from all fifteen individuals, the probability they come from Family Y is \frac{5}{15}, which also simplifies to \frac{1}{3}. This says P(D) = \frac{1}{3}.
In other words, knowledge of C is irrelevant to the probability of D occurring, which means C and D are independent.
The average score on this problem was 35%.
At the reunion, the Tritons play a game that involves placing the four letters into a hat (W, X, Y, and Z, corresponding to the four families). Then, five times, they draw a letter from the hat, write it down on a piece of paper, and place it back into the hat.
Let p = \frac{1}{4} in the questions that follow.
What is the probability that Family W is selected all 5 times?
p^5
1 - p^5
1 - (1 - p)^5
(1 - p)^5
p \cdot (1 - p)^4
p^4 (1 - p)
None of these.
Answer: p^5
The probability of selecting Family W in the first round is p, which is the same for the second round, the third round, and so on. Each of the chosen letters is drawn independently from the others because the result of one draw does not affect the result of the next. We can apply the multiplication rule here and multiply the probabilities of choosing Family W in each round. This comes out to be p\cdot p\cdot p\cdot p\cdot p, which is p^5.
The average score on this problem was 91%.
What is the probability that Family W is selected at least once?
p^5
1 - p^5
1 - (1 - p)^5
(1 - p)^5
p \cdot (1 - p)^4
p^4 (1 - p)
None of these.
Answer: 1 - (1 - p)^5
Since there are too many ways that Family W can be selected to meet the condition that it is selected at least once, it is easier if we calculate the probability that Family W is never selected and subtract that from 1. The probability that Family W is not selected in the first round is 1-p, which is the same for the second round, the third round, and so on. We want this to happen for all five rounds, and since the events are independent, we can multiply their probabilities all together. This comes out to be (1-p)^5, which represents the probability that Family W is never selected. Finally, we subtract (1-p)^5 from 1 to find the probability that Family W is selected at least once, giving the answer 1 - (1-p)^5.
The average score on this problem was 62%.
What is the probability that Family W is selected exactly once, as the last family that is selected?
p^5
1 - p^5
1 - (1 - p)^5
(1 - p)^5
p \cdot (1 - p)^4
p^4 (1 - p)
None of these.
Answer: p \cdot (1 - p)^4
We want to find the probability of Family W being selected only as the last draw, and not in the first four draws. The probability that Family W is not selected in the first draw is (1-p), which is the same for the second, third, and fourth draws. For the fifth draw, the probability of choosing Family W is p. Since the draws are independent, we can multiply these probabilities together, which comes out to be (1-p)^4 \cdot p = p\cdot (1-p)^4.
The average score on this problem was 67%.
We’ll be looking at a DataFrame named sungod that
contains information on the artists who have performed at Sun God in
years past. For each year that the festival was held, we have
one row for each artist that performed that year. The columns
are:
'Year' (int): the year of the
festival'Artist' (str): the name of the
artist'Appearance_Order' (int): the order in
which the artist appeared in that year’s festival (1 means they came
onstage first)The rows of sungod are arranged in no particular
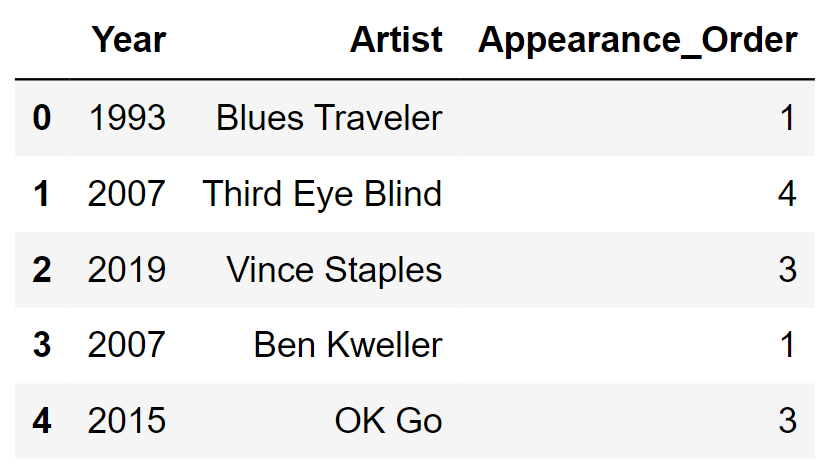
order. The first few rows of sungod are shown
below (though sungod has many more rows
than pictured here).
Assume:
'Year' of 2015 and an
'Appearance_Order' of 3).import babypandas as bpd and
import numpy as np. Fill in the blank in the code below so that
chronological is a DataFrame with the same rows as
sungod, but ordered chronologically by appearance on stage.
That is, earlier years should come before later years, and within a
single year, artists should appear in the DataFrame in the order they
appeared on stage at Sun God. Note that groupby
automatically sorts the index in ascending order.
chronological = sungod.groupby(___________).max().reset_index() ['Year', 'Artist', 'Appearance_Order']
['Year', 'Appearance_Order']
['Appearance_Order', 'Year']
None of the above.
Answer:
['Year', 'Appearance_Order']
The fact that groupby automatically sorts the index in
ascending order is important here. Since we want earlier years before
later years, we could group by 'Year', however if we
just group by year, all the artists who performed in a given
year will be aggregated together, which is not what we want. Within each
year, we want to organize the artists in ascending order of
'Appearance_Order'. In other words, we need to group by
'Year' with 'Appearance_Order' as subgroups.
Therefore, the correct way to reorder the rows of sungod as
desired is
sungod.groupby(['Year', 'Appearance_Order']).max().reset_index().
Note that we need to reset the index so that the resulting DataFrame has
'Year' and 'Appearance_Order' as columns, like
in sungod.
The average score on this problem was 85%.
Another DataFrame called music contains a row for every
music artist that has ever released a song. The columns are:
'Name' (str): the name of the music
artist'Genre' (str): the primary genre of the
artist'Top_Hit' (str): the most popular song by
that artist, based on sales, radio play, and streaming'Top_Hit_Year' (int): the year in which
the top hit song was releasedYou want to know how many musical genres have been represented at Sun
God since its inception in 1983. Which of the following expressions
produces a DataFrame called merged that could help
determine the answer?
merged = sungod.merge(music, left_on='Year', right_on='Top_Hit_Year')
merged = music.merge(sungod, left_on='Year', right_on='Top_Hit_Year')
merged = sungod.merge(music, left_on='Artist', right_on='Name')
merged = music.merge(sungod, left_on='Artist', right_on='Name')
Answer:
merged = sungod.merge(music, left_on='Artist', right_on='Name')
The question we want to answer is about Sun God music artists’
genres. In order to answer, we’ll need a DataFrame consisting of rows of
artists that have performed at Sun God since its inception in 1983. If
we merge the sungod DataFrame with the music
DataFrame based on the artist’s name, we’ll end up with a DataFrame
containing one row for each artist that has ever performed at Sun God.
Since the column containing artists’ names is called
'Artist' in sungod and 'Name' in
music, the correct syntax for this merge is
merged = sungod.merge(music, left_on='Artist', right_on='Name').
Note that we could also interchange the left DataFrame with the right
DataFrame, as swapping the roles of the two DataFrames in a merge only
changes the ordering of rows and columns in the output, not the data
itself. This can be written in code as
merged = music.merge(sungod, left_on='Name', right_on='Artist'),
but this is not one of the answer choices.
The average score on this problem was 86%.
Consider an artist that has only appeared once at Sun God. At the time of their Sun God performance, we’ll call the artist
Complete the function below so it outputs the appropriate description for any input artist who has appeared exactly once at Sun God.
def classify_artist(artist):
filtered = merged[merged.get('Artist') == artist]
year = filtered.get('Year').iloc[0]
top_hit_year = filtered.get('Top_Hit_Year').iloc[0]
if ___(a)___ > 0:
return 'up-and-coming'
elif ___(b)___:
return 'outdated'
else:
return 'trending'What goes in blank (a)?
Answer: top_hit_year - year
Before we can answer this question, we need to understand what the
first three lines of the classify_artist function are
doing. The first line creates a DataFrame with only one row,
corresponding to the particular artist that’s passed in as input to the
function. We know there is just one row because we are told that the
artist being passed in as input has appeared exactly once at Sun God.
The next two lines create two variables:
year contains the year in which the artist performed at
Sun God, andtop_hit_year contains the year in which their top hit
song was released.Now, we can fill in blank (a). Notice that the body of the
if clause is return 'up-and-coming'. Therefore
we need a condition that corresponds to up-and-coming, which we are told
means the top hit came out after the artist appeared at Sun God. Using
the variables that have been defined for us, this condition is
top_hit_year > year. However, the if
statement condition is already partially set up with > 0
included. We can simply rearrange our condition
top_hit_year > year by subtracting year
from both sides to obtain top_hit_year - year > 0, which
fits the desired format.
The average score on this problem was 89%.
What goes in blank (b)?
Answer: year-top_hit_year > 5
For this part, we need a condition that corresponds to an artist
being outdated which happens when their top hit came out more than five
years prior to their appearance at Sun God. There are several ways to
state this condition: year-top_hit_year > 5,
year > top_hit_year + 5, or any equivalent condition
would be considered correct.
The average score on this problem was 89%.
You’re definitely going to Sun God 2022, but you don’t want to go alone! Fortunately, you have n friends who promise to go with you. Unfortunately, your friends are somewhat flaky, and each has a probability p of actually going (independent of all others). What is the probability that you wind up going alone? Give your answer in terms of p and n.
Answer: (1-p)^n
If you go alone, it means all of your friends failed to come. We can think of this as an and condition in order to use multiplication. The condition is: your first friend doesn’t come and your second friend doesn’t come, and so on. The probability of any individual friend not coming is 1-p, so the probability of all your friends not coming is (1-p)^n.
The average score on this problem was 76%.
In past Sun God festivals, sometimes artists that were part of the lineup have failed to show up! Let’s say there are n artists scheduled for Sun God 2022, and each artist has a probability p of showing up (independent of all others). What is the probability that the number of artists that show up is less than n, meaning somebody no-shows? Give your answer in terms of p and n.
Answer: 1-p^n
It’s actually easier to figure out the opposite event. The opposite of somebody no-showing is everybody shows up. This is easier to calculate because we can think of it as an and condition: the first artist shows up and the second artist shows up, and so on. That means we just multiply probabilities. Therefore, the probability of all artists showing up is p^n and the probability of some artist not showing up is 1-p^n.
The average score on this problem was 73%.